[USACO 2020 US Open Platinum] Circus
一、题目
二、解法
考虑把所有元素集中在 \(1,2...k\) 中,我们称之为本源状态,我们希望找到从一个本源状态出发可以到达其他的本源状态数。考虑对于两个元素 \((x,y)\),如果可以在其他元素保持不变的情况下交换它们,就把他们划分在一个等价类中,那么一个等价类中的元素可以任意交换,所以要除去它们内部的顺序,设等价类的大小为 \(s_i\),则答案是:
寻找 \((x,y)\) 能够交换的必要条件,考虑树上的一条极长的二度链,设二度链的长度为 \(l\),它的端点分别是 \(u,v\),端点 \(u,v\) 对应的子树大小分别是 \(A,B\):
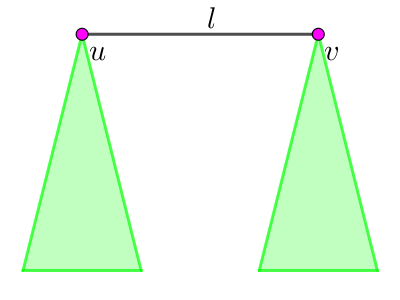
当 \(k\geq n-l-1\) 时,\(k\geq (A-1)+(B-1)\),我们把其他点都填满在 \(u,v\) 的子树中(不含 \(u,v\) 两端点),那么链上会有 \(k-(n-l-1)\) 个点,并且这些点的相对顺序是不会改变的(特别地 \(k=n-l-1\) 也成立)
所以我们可以得到必要条件:对于任意满足 \(k\geq n-l-1\) 的二度链,\((x,y)\) 必须同在 \(u\) 或者 \(v\) 的子树内(不含 \(u,v\) 两端点),充分性证明需要构造和讨论,可以参考 yhx的博客,有图解应该是比较好懂的。
为了计算答案,我们可以把满足 \(l\geq n-k-1\) 的极长二度链断开,然后原图会形成若干个连通块。
考虑第 \(i\) 个连通块的大小是 \(|C_i|\),我们计算可以到达它的点数。考虑以这个连通块为根,统计每一个子树的贡献(这里是相对原树而言的,不考虑断边),设其中一个子树大小为 \(sz\),子树总个数为 \(y\),那么我们肯定会把元素堆在剩下 \(n-sz-1\) 个点中(注意也不能放在点 \(u\),所以要减 \(1\)),所以不能到达它的点数就是 \(k-(n-sz-1)\),那么不能到达它的点数总和就是:
所以可以到达它的点数总和就是 \(k-[(k-n+1)\cdot y+(n-|C_i|)]=(n-k-1)\cdot (y-1)+|C_i|-1\)
考虑从小到大枚举 \(n-k-1\),然后连接 \(l<n-k-1\) 的二度链,用并查集维护联通块的大小和度数(即上文中的子树个数),计算答案时可以暴力枚举所有连通块,因为连通块个数等于还未加入的二度链数\(+1\),那么一个二度链只会贡献其长度次的查询,所以暴力的次数不超过 \(O(n)\),时间复杂度 \(O(n\log n)\)
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <set>
using namespace std;
const int M = 100005;
const int MOD = 1e9+7;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,fac[M],inv[M],key[M],deg[M],dep[M];
int rt,p[M],fa[M],siz[M],ans[M];
vector<int> g[M];set<int> s;
struct node{int l,u,v;}a[M];
void init(int n)
{
fac[0]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
for(int i=2;i<=n;i++) inv[i]=inv[i-1]*inv[i]%MOD;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;
}
void dfs(int u)
{
for(int v:g[u]) if(v^p[u])
p[v]=u,dep[v]=dep[u]+1,dfs(v);
}
int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
void merge(int u,int v,int c)
{
int x=find(u),y=find(v);
fa[x]=y;siz[y]+=siz[x]+c-1;
deg[y]+=deg[x]-2;s.erase(x);
}
signed main()
{
n=read();init(n);
for(int i=1;i<n;i++)
{
int u=read(),v=read();
g[u].push_back(v);deg[u]++;
g[v].push_back(u);deg[v]++;
}
for(int i=1;i<=n;i++) if(deg[i]!=2)
key[i]=1,s.insert(rt=i);
dfs(rt);
for(int i=1;i<=n;i++) if(key[i] && i!=rt)
{
int v=0;
for(v=p[i];!key[v];v=p[v]);
a[++m]=node{dep[i]-dep[v],v,i};
}
sort(a+1,a+1+m,[&](node a,node b)
{return a.l<b.l;});
for(int i=1;i<=n;i++)
fa[i]=i,siz[i]=1,ans[i]=fac[i];
for(int i=0,j=1;i<n-1;i++)
{
while(j<=m && a[j].l<i)
merge(a[j].u,a[j].v,a[j].l),j++;
int &t=ans[n-i-1];
for(int x:s)
t=t*inv[i*(deg[x]-1)+siz[x]-1]%MOD;
}
for(int i=1;i<=n;i++)
printf("%lld\n",ans[i]);
}




