AtCoder Grand Contest 018&019
018E Sightseeing Plan
题目描述
解法
考虑枚举中转点 \(P\)，那么对应的路径数是：\(P\) 到第一个矩形的方案数 \(\times\) \(P\) 到第二个矩形的方案数。
可以以 \(P\) 建立平面直角坐标系，那么可以差分成四个矩形，问题变成了在矩形内停下的方案数：
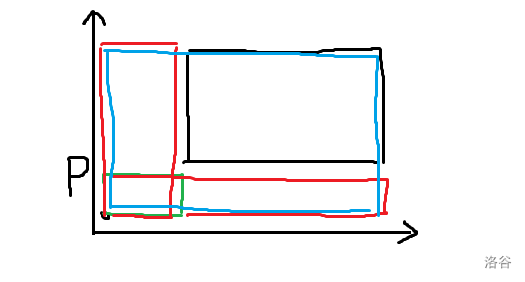
设矩形右上角的坐标是 \((n,m)\)，那么显然方案数是 \(\sum_{i=0}^{n}\sum_{j=0}^m{i+j\choose i}\)
应用组合意义来化简，考虑组合意义是 \(i\) 个球依次添加了 \(0\sim m\) 个球，然后要从中选出 \(i\) 个球。再新增一个球表示添加到哪里了，可以转化成 \(i+m+1\) 个球中选择 \(i+1\) 个球，即 \(\sum_{j=0}^m {i+j\choose i}={i+m+1\choose i+1}={i+m+1\choose m}\)
再次应用同样的组合意义，我们可以得到 \(\sum_{i=0}^n{i+m+1\choose m}={n+m+2\choose m+1}\)
发现这就是 \((0,0)\) 到 \((n+1,m+1)\) 的方案数，所以我们可以把矩形拆分成四个点，计算点到点的方案数。
回到原问题，我们成功地把问题转化成了：固定起点和终点，一条路径的贡献是其在给定矩形内的长度 \(+1\)，求所有路径的贡献和。枚举中转点太慢了，我们只需要知道一条路径在哪里进入矩形，在哪里离开矩形，就可以知道在矩形内的长度。
发现这两部分又可以拆分计算，因为长度可以看成曼哈顿距离，所以进入和出去的路径都贡献 横纵坐标之和 次即可。
枚举进入矩形的点 \((x_3,i)/(i,y_3)\)，那么有这样的负贡献：起点到 \((x_3-1,i)\) 的方案数 $\times $ \((x_3,i)\) 到终点的方案数 \(\times (x_3+i)\)
枚举离开矩形的点 \((x_4,i)/(i,y_4)\)，那么有这样的正贡献：起点到 \((x_4,i)\) 的方案数 $\times $ \((x_4+1,i)\) 到终点的方案数 \(\times (x_4+i+1)\)
时间复杂度 \(O(n)\)
#include <cstdio>
const int M = 2000005;
const int MOD = 1e9+7;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int x[7],y[7],x3,x4,y3,y4,ans,fac[M],inv[M];
struct node{int x,y,f;}s[10];
void init(int n)
{
fac[0]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
for(int i=1;i<=n;i++) inv[i]=inv[i-1]*inv[i]%MOD;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;
}
int Abs(int x) {return x>0?x:-x;}
int C(int n,int m)
{
if(n<m || m<0) return 0;
return fac[n]*inv[m]%MOD*inv[n-m]%MOD;
}
int G(int x1,int y1,int x2,int y2)
{
int x=Abs(x2-x1),y=Abs(y2-y1);
return C(x+y,x);
}
void add(int &x,int y) {x=(x+y%MOD+MOD)%MOD;}
int zxy(int x1,int y1,int x2,int y2)
{
int r=0;
for(int x=x3;x<=x4;x++)
{
add(r,G(x1,y1,x,y4)*G(x,y4+1,x2,y2)%MOD*(x+y4+1));
add(r,-G(x1,y1,x,y3-1)*G(x,y3,x2,y2)%MOD*(x+y3));
}
for(int y=y3;y<=y4;y++)
{
add(r,G(x1,y1,x4,y)*G(x4+1,y,x2,y2)%MOD*(x4+y+1));
add(r,-G(x1,y1,x3-1,y)*G(x3,y,x2,y2)%MOD*(x3+y));
}
return r;
}
signed main()
{
init(2000000);
for(int i=1;i<=6;i++) x[i]=read();
for(int i=1;i<=6;i++) y[i]=read();
x3=x[3];y3=y[3];x4=x[4];y4=y[4];
s[1]=node{x[1]-1,y[1]-1,1};
s[2]=node{x[1]-1,y[2],-1};
s[3]=node{x[2],y[1]-1,-1};
s[4]=node{x[2],y[2],1};
//
s[5]=node{x[5],y[5],1};
s[6]=node{x[6]+1,y[5],-1};
s[7]=node{x[5],y[6]+1,-1};
s[8]=node{x[6]+1,y[6]+1,1};
//
for(int a=1;a<=4;a++) for(int b=5;b<=8;b++)
add(ans,s[a].f*s[b].f*
zxy(s[a].x,s[a].y,s[b].x,s[b].y));
printf("%lld\n",ans);
}
019F Yes or No
题目描述
解法
考虑一个朴素的 \(dp\)，设 \(dp[i][j]\) 表示有 \(i\) 个问题是 YES，有 \(j\) 个问题是 NO，最优策略一定是猜测较多的那一个，但是答案可以看成是随机的，所以有转移：
显然这东西是具有对称性的：\(dp[i][j]=dp[j][i]\)，考虑它的组合意义，就是在 \(n\times m\) 的路径上行走，从起点 \((n,m)\) 到终点 \((0,0)\)，每次可以向下或者向右走一步，每种路径有其对应的权值。
考虑对每种路径分别统计权值，有一个关键的 \(\tt observation\) 是：不妨设 \(n\geq m\)，如果路径始终在 \(y=x\) 的上方，那么贡献一定是 \(n\)，这是因为最优策略总是选 YES
那么对于穿过 \(y=x\) 的路径，根据前文所提到的对称性，我们把它翻折上去。但是这样会漏算一小部分的贡献，因为在 \((x,x)\) 的这一步一定不会被我们统计任何贡献，而实际上它是有一个 \(\frac{\max(i,j)}{i+j}=\frac{1}{2}\) 的贡献的，要把它算上去。
那么问题就转化成了统计 \(y=x\) 被穿过的总次数，被穿过一次就多 \(\frac{1}{2}\) 的贡献，所以答案是：
时间复杂度 \(O(n)\)
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 1000005;
const int MOD = 998244353;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,ans,fac[M],inv[M];
void init(int n)
{
fac[0]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
for(int i=1;i<=n;i++) inv[i]=inv[i-1]*inv[i]%MOD;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;
}
void add(int &x,int y) {x=(x+y)%MOD;}
int C(int n,int m)
{
if(n<m || m<0) return 0;
return fac[n]*inv[m]%MOD*inv[n-m]%MOD;
}
int qkpow(int a,int b)
{
int r=1;
while(b>0)
{
if(b&1) r=r*a%MOD;
a=a*a%MOD;
b>>=1;
}
return r;
}
signed main()
{
n=read();m=read();init(n+m);
if(n<m) swap(n,m);
for(int i=1;i<=m;i++)
add(ans,C(m-i+n-i,m-i)*C(2*i,i));
ans=ans*qkpow(2*C(n+m,n)%MOD,MOD-2)%MOD;
printf("%lld\n",(ans+n)%MOD);
}
