#24 CF1438F & CF1608F & CF1264D

Olha and Igor

题目描述

点此看题

解法

自己想了一个 $O(n^2)$ 的做法，好像也要基于 $\tt lca$ 的出现频率这东西（多少沾点边了）

考虑询问 $(u,v,w)$ 的另一种意义：在树上找到点 $x$，使得 $d(u,x)+d(v,x)+d(w,x)$ 最小。

发现如果我们随机三个不同的点问一次 $(u,v,w)$，考虑分析得到的结果：

• 不可能是叶子。
• 如果返回的 $x$ 是真正的根，必须要其中一个点恰好是根，另外两个点分居左右子树。
• 如果其中两个点的 $\tt lca$ 是左儿子，另外一个点在右子树，一定直接得到根的左儿子。
• 如果其中两个点的 $\tt lca$ 是右儿子，另外一个点在左子树，一定直接得到根的右儿子。
• 根据数感，出现其他的概率远小于根的左右儿子情况（概率可以计算出来，但是我懒）

那么我们可以随机 $420$ 次，认为出现频率最大的两个点就是根的左右儿子。设得到了 $x,y$，那么我们枚举根，如果询问 $(x,y,i)$ 得到 $i$，那么 $i$ 就是真正的根，发现最坏情况下询问次数 $n+420$

#include <cstdio>
#include <random>
#include <algorithm>
using namespace std;
const int M = 1000005;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,h,a[M],p[M];
int ask(int u,int v,int w)
{
	printf("? %d %d %d\n",u,v,w);
	fflush(stdout);
	return read();
}
signed main()
{
	h=read();n=(1<<h)-1;
	mt19937 z(114514);
	for(int i=0;i<420;i++)
	{
		int u=z()%n+1,v=z()%n+1,w=z()%n+1;
		while(u==v) v=z()%n+1;
		while(u==w || v==w) w=z()%n+1;
		a[ask(u,v,w)]++;
	}
	for(int i=1;i<=n;i++) p[i]=i;
	sort(p+1,p+1+n,[&](int i,int j)
	{return a[i]>a[j];});
	int x=p[1],y=p[2];
	for(int i=1;i<=n;i++)
		if(i!=x && i!=y && ask(x,y,i)==i)
		{
			printf("! %d\n",i);
			fflush(stdout);
			return 0;
		}
}

MEX counting

题目描述

点此看题

解法

如果用计数 $dp$ 的话，那么我们需要在规划完前缀 $i$ 时得到它的 $mex$，所以我们考虑使用如下的计数顺序：对于某一种序列 $a_1,a_2...a_n$，我们在 $mex(j)\geq a_i$ 的第一个位置 $j$ 来确定 $a_i$ 的值，这样也能方便地确定 $mex$

设 $f(i,j,k)$ 表示对于前 $i$ 个位置，还有 $j$ 种值未确定，$mex(i)=k$ 的方案数，转移讨论 $a_i$ 取什么：

• $a_i<k$，对 $mex$ 不会造成影响：$f(i+1,j,k)\leftarrow f(i,j,k)\cdot k$
• $a_i>k$，对 $mex$ 不会造成影响，但是还要考虑它是归入已有的未确定的值中：$f(i+1,j,k)\leftarrow f(i,j,k)\cdot j$ ；还是新增一种未确定的值：$f(i+1,j+1,k)\leftarrow f(i,j,k)$
• $a_i=k$，我们枚举 $mex$ 变化成 $t(t>k)$，那么就需要那未确定的值来填补 $(k,t)$ 的这一段，方案数就是排列数 $A_{j}^{k-t-1}$：$f(i+1,j-(t-k-1),t)\leftarrow f(i,j,k)\cdot \frac{j!}{(j-(k-t-1))!}$

暴力转移复杂度 $O(n^4)$，可以利用题目中 $K\leq 50$ 的条件，也就是 $mex(i)$ 的取值最多只有 $100$ 种，所以时间复杂度优化到了 $O(n^2k^2)$

我们还需要优化最后一种转移，我们把状态的第二维偏移一下，$f'(i,j+k,k)=f(i,j,k)$，最后一种转移就能写成前缀和的形式，这样我们只需要对第三维做前缀和即可：

$$f'(i+1,j+1,t)\leftarrow f'(i,j,k)\cdot\frac{(j-k)!}{(j-t)!}$$

其它种类的转移也用这种形式写出：

$$f'(i+1,j,k)\leftarrow j\cdot f'(i,j,k)$$

$$f'(i+1,j+1,k)\leftarrow f'(i,j,k)$$

时间复杂度 $O(n^2k)$，需要使用滚动数组优化空间复杂度。

#include <cstdio>
#include <iostream>
using namespace std;
const int M = 2005;
const int MOD = 998244353;
#define int long long
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,k,ans,l[M],r[M],fac[M],inv[M];
int dp[2][M][M],s[2][M][M];
void add(int &x,int y) {x=(x+y)%MOD;}
void init(int n)
{
	fac[0]=inv[0]=inv[1]=1;
	for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;
	for(int i=2;i<=n;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
	for(int i=2;i<=n;i++) inv[i]=inv[i-1]*inv[i]%MOD;
}
signed main()
{
	init(2000);n=read();k=read();
	for(int i=1;i<=n;i++)
	{
		int x=read();
		l[i]=max(0ll,x-k);
		r[i]=min(i,x+k);
	}
	dp[0][0][0]=s[0][0][0]=1;
	for(int i=1,w=1;i<=n;i++,w^=1)
	{
		for(int j=0;j<=i;j++)
		for(int k=l[i];k<=r[i] && k<=j;k++)
		{
			add(dp[w][j][k],j*dp[w^1][j][k]);
			if(j) add(dp[w][j][k],dp[w^1][j-1][k]);
			if(j&&k) add(dp[w][j][k],s[w^1][j-1][min(k-1,r[i-1])]*inv[j-k]);
			add(s[w][j][k],dp[w][j][k]*fac[j-k]);
			if(k) add(s[w][j][k],s[w][j][k-1]);
		}
		for(int j=0;j<i;j++)
			for(int k=l[i-1];k<=r[i-1] && k<=j;k++)
				dp[w^1][j][k]=s[w^1][j][k]=0;
	}
	for(int i=0;i<=n;i++)
		for(int j=l[n];j<=r[n] && j<=i;j++)
			add(ans,dp[n&1][i][j]*fac[n-j]%MOD*inv[n-i]);
	printf("%lld\n",ans);
}

Beautiful Bracket Sequence

题目描述

点此看题

解法

考虑对于一个确定的括号序列如何计算其深度，策略肯定是把第一个左括号和最后一个右括号匹配起来然后让深度增加 $1$，这样一定存在一个分界线 $i\in[1,n)$，使得 $i$ 左边的左括号和 $i$ 右边的右括号匹配。

关键结论是：一定存在 $i$ 使得左边的左括号数量等于右边的右括号数量，这样的 $i$ 唯一且最优，证明可以考虑下面的图像：

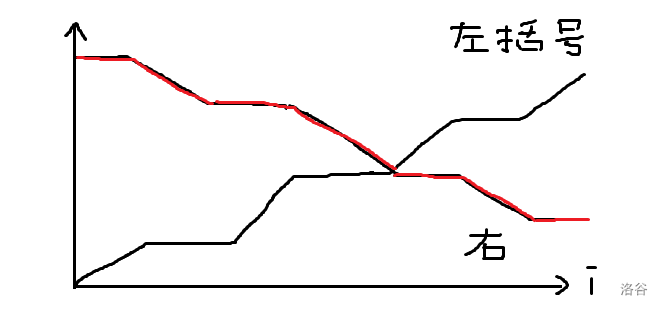
交点最优且唯一的原因是，两条折线的变化率总是 $0/1$，并且起点右高左低，终点左高右低。

那么直接上贡献法，设 $l,x$ 分别表示左边的左括号数和问号数，$r,y$ 分别表示右边的右括号数和问号数，枚举分界线 $i$，考虑它的贡献是：

$$\sum_{i=0}^{x}(l+i){x\choose i}{y\choose l+i-r}$$

感觉就很能范德蒙德卷积优化，所以我们把它拆成两部分，然后变形：

$$\begin{aligned}&\sum_{i=0}^{x}l{x\choose i}{y\choose l+i-r}+\sum_{i=0}^{x}i{x\choose i}{y\choose l+i-r}\\=&l\sum_{i=0}^{x}{x\choose i}{y\choose l+i-r}+x\sum_{i=0}^{x}{x-1\choose i-1}{y\choose l+i-r}\\=&l\sum_{i=0}^{x}{x\choose i}{y\choose y-l-i+r}+x\sum_{i=0}^{x}{x-1\choose i-1}{y\choose y-l-i+r}\\=&l\cdot{x+y\choose y-l+r}+x\cdot{x+y-1\choose y-l+r-1}\end{aligned}$$

时间复杂度 $O(n)$

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 1000005;
const int MOD = 998244353;
#define int long long
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,fac[M],inv[M],pl[M],pr[M],pq[M];char s[M];
void init(int n)
{
	fac[0]=inv[0]=inv[1]=1;
	for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;
	for(int i=2;i<=n;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
	for(int i=2;i<=n;i++) inv[i]=inv[i-1]*inv[i]%MOD;
}
int C(int n,int m)
{
	if(n<m || m<0) return 0;
	return fac[n]*inv[m]%MOD*inv[n-m]%MOD;
}
signed main()
{
	scanf("%s",s+1);
	n=strlen(s+1);init(n);
	for(int i=1;i<=n;i++)
	{
		pl[i]=pl[i-1]+(s[i]=='(');
		pr[i]=pr[i-1]+(s[i]==')');
		pq[i]=pq[i-1]+(s[i]=='?');
	}
	int ans=0;
	for(int i=1;i<n;i++)
	{
		int l=pl[i],r=pr[n]-pr[i];
		int x=pq[i],y=pq[n]-pq[i];
		ans=(ans+l*C(x+y,y+r-l)
		+x*C(x+y-1,y-l+r-1))%MOD;
	}
	printf("%lld\n",ans);
}