[省选集训2022] 模拟赛16
小Z与函数
题目描述
在 \(2022/3/24\) 上午,\(\tt zxy\) 看到了一个函数:
int get(int n)
{
int res=0;
for(int i=1;i<=n;i++)
{
int vs=0;
for(int j=i;j<=n;j++) if(a[i]<a[j])
swap(a[i],a[j]),res++,vs=1;
res+=vs;
}
return res;
}
有一个长度为 \(n\) 的序列 \(a\),对于 \(a\) 的每个前缀,将其作为一个序列 \(a\) 所求得的函数值是多少?
\(T\leq 5,1\leq n\leq 2\cdot 10^5,1\leq a_i\leq n\)
解法
社论:我都会做的题一定是垃圾题。我们可以把总次数分成 \(\tt swap\) 和 \(\tt vs\) 两部分分别解决。
首先考虑 \(\tt swap\) 的次数,其实就是每个点前面比它小的值的个数之和(相同的值要去重),不难证明。
然后发现这个 \(\tt vs\) 很难做,好像单次计算都要 \(O(n^2)\),那么我们不妨先考虑如何动态插入,达成总时间复杂度 \(O(n^2)\) 的目标。考虑新加入的数对前面的影响,因为选择排序原来是选出一个极长上升子序列,然后做这样的变化:
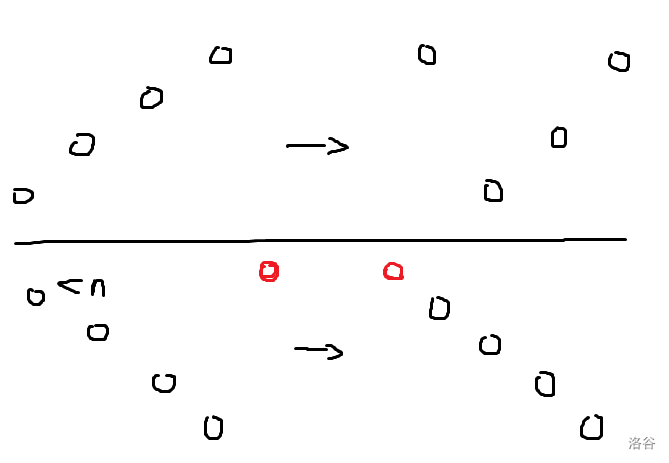
上图分别展示了,正常选择排序时的变化,和我们在序列末尾插入(用红点表示)对前面的影响。从插入的角度看,我们是选出一个极长下降子序列(首项为第一个 \(<\) 插入值的数),然后子序列对应的位置都会产生一次交换。
如果你理解了上面的过程,就不难写出 \(O(n^2)\) 的优秀算法:
for(int i=1;i<=n;i++)
{
for(int j=1;j<i;j++) if(a[j]<a[i])
{
swap(a[j],a[i]);ans++;
if(!b[j]) ans++;b[j]|=1;
}
printf("%d ",ans);
}
取出一个极长下降子序列是很难得,但是考虑到每个位置只会被覆盖一次,我们考虑使用势能法,把未覆盖的位置作为势能来让复杂度正确。有一个关键的 \(\tt observation\) 是,如果某个值 \(x\) 在极长下降子序列中去覆盖某个位置,而这个位置先前已经被覆盖过的话,\(x\) 的覆盖以后都不起作用。因为这样一定是存在一个比 \(x\) 小的数先前就把这个位置覆盖过,那么这个较小数一定抢先覆盖了所有 \(x\) 未来所有可能覆盖到的位置。
所以我们维护一个关于值的 \(\tt set\),每次暴力扫描,用树状数组维护排名,那么要么删除这个值,要么覆盖一个位置。根据势能法,时间复杂度 \(O(n\log n)\),代码实现极为简洁。
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <set>
using namespace std;
const int M = 200005;
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
void write(ll x)
{
if(x>=10) write(x/10);
putchar(x%10+'0');
}
int T,n,a[M],b[M],use[M];
struct fenwick
{
int b[M];
fenwick() {memset(b,0,sizeof b);}
void clear() {memset(b,0,sizeof b);}
void add(int x)
{
for(int i=x;i<=n;i+=i&(-i)) b[i]++;
}
int ask(int x)
{
int r=0;
for(int i=x;i>0;i-=i&(-i)) r+=b[i];
return r;
}
}A,B;
void work()
{
n=read();long long ans=0;
set<int> s;A.clear();B.clear();
for(int i=1;i<=n;i++)
a[i]=read(),b[i]=use[i]=0;
for(int i=1;i<=n;i++)
{
vector<int> d;
for(auto &x:s)
{
if(x>=a[i]) break;
int p=i-B.ask(x);
if(!b[p]) b[p]=1,ans++;
else if(b[p]) d.push_back(x);
}
for(auto &x:d) s.erase(x);
int y=a[i];ans+=A.ask(y-1);
if(!use[y])
s.insert(y),A.add(y),use[y]=1;
B.add(y);
write(ans),putchar(' ');
}
puts("");
}
signed main()
{
freopen("function.in","r",stdin);
freopen("function.out","w",stdout);
T=read();
while(T--) work();
}
游戏
题目描述
有 \(n\) 个数的排列,首先进行 \(n\) 次操作,从小到大地把排列中的数插入到 \(a\) 序列的前端或者末尾。然后再进行 \(n\) 次操作,把 \(a\) 序列的前端或者末尾插入到 \(b\) 序列的末尾。
问有多少种可能被生成的 \(b\) 序列,使得第 \(k\) 位是 \(1\),答案对大质数取模。
\(k\leq n\leq 5\cdot 10^5\)
解法
既然 \(1\) 的位置是关键的,我们按照 \(1\) 的位置把 \(b\) 序列划分成两半。首先我们考虑检验 \(b\) 的前半段是否合法,考虑逆向操作,每次把 \(b\) 的首项插入到 \(a\) 中。
考虑 \(a\) 的结构一定是从 \(1\) 分开,前面是单调递减,后面是单调递增。那么把 \(b\) 插入时,可以看成对两个独立的单调递减序列在末尾插入。并且这个插入是有最优策略的,如果两边都可以插入,我们贪心地选择值较小的那一边插入,这个插入过程是由唯一策略的,所以可以根据插入过程来计数。
考虑到反序表可以唯一的表示排列,所以我们在规划 \(b\) 时考虑 \(b\) 的反序表 \(d_i\),如果 \(d_i\) 等于 \(0\),那么值小的那一方会接上 \(i\);否则 \(i\) 会接到另一边,我们可以记录下夹在两个末尾中间数的个数,如图(下面是 \(d+1\),对不起标错了):
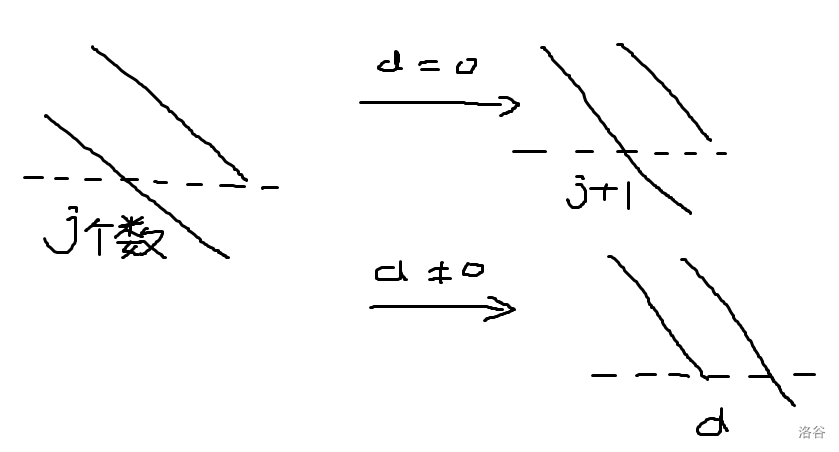
设 \(dp[i][j]\) 表示考虑了前 \(i\) 个数,有 \(j\) 个数夹在中间的方案数,转移:
设 \(suf[i][j]=\sum_{k=j}^i dp[i][k]\),那么把转移写成后缀和的形式:
考虑上式的组合意义,可以对上式进行变换,可以得到卡特兰数的形式:
那么就是向上走一格或者向右走一格,要求范围在 \([0,i)\) 中的方案数,就是普通的卡特兰数了。这样我们可以求出 \(dp[k-1][i]\),就成功地解决了前半部分,考虑 \(1\) 一定会接在值小的序列末尾,而剩下的数会接在另一个序列末尾。
根据上面的大小关系我们可以知道选出后半段数的方案是 \({i+(n-k)\choose n-k}\) 的,再乘上任意按按钮的方案数是 \(2^{\max(0,n-k-1)}\)(考虑 \(a\) 生成 \(b\) 的过程),时间复杂度 \(O(n)\)
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 1000005;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,k,MOD,ans,fac[M],inv[M],pw[M];
void init(int n)
{
fac[0]=inv[0]=inv[1]=pw[0]=1;
for(int i=1;i<=n;i++) pw[i]=pw[i-1]*2%MOD;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;
for(int i=2;i<=n;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
for(int i=2;i<=n;i++) inv[i]=inv[i]*inv[i-1]%MOD;
}
int C(int n,int m)
{
if(n<m || m<0) return 0;
return fac[n]*inv[m]%MOD*inv[n-m]%MOD;
}
int walk(int n,int m)
{
m=n-m;
return (C(n+m,n)-C(n+m,n+1)+MOD)%MOD;
}
signed main()
{
freopen("game.in","r",stdin);
freopen("game.out","w",stdout);
n=read();k=read();MOD=read();init(1e6);
if(k==1)
{
printf("%lld\n",pw[max(0ll,n-2)]);
return 0;
}
for(int i=1;i<k;i++)
{
int dp=(walk(k-1,i)-walk(k-1,i+1)+MOD)%MOD;
ans=(ans+dp*C(i+n-k,n-k)%MOD*pw[max(0ll,n-k-1)])%MOD;
}
printf("%lld\n",ans);
}




