[做题笔记] 退役前的思维题小练
CF1368E Ski Accidents
题目描述
解法
考虑按如下方法把点划分成三个集合 \(A,B,C\):
- \(A\):入度为 \(0\) 或者只有来自 \(C\) 的入边。
- \(B\):至少有一条来自 \(A\) 的入边并且没有来自 \(B\) 的入边。
- \(C\):至少有一条来自 \(B\) 的入边。
初始把入度为 \(0\) 的点设置为 \(A\),然后按照染色的方式跑出 \(B,C\),最后把剩下的点加入 \(A\) 即可。
发现如果我们删除 \(C\),满足 \(A,B\) 集合自身没有边,所以路径长度 \(\leq 1\);并且由于 \(2|A|\geq |B|\),\(2|B|\geq |C|\),所以 \(|C|\leq \frac{4}{7}n\),那么点数也是满足条件的。
这个做法是怎么得来的呢?\(\tt OUYE\) 的一句话让人醍醐灌顶:考虑一个有 \(7\) 个点的完全二叉树。
#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
const int M = 200005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int T,n,m,k,p[M],c[M];vector<int> g[M];
void work()
{
n=read();m=read();k=0;
for(int i=1;i<=n;i++)
c[i]=0,g[i].clear();
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
g[u].push_back(v);
}
for(int u=1;u<=n;u++) for(int v:g[u])
{
if(c[u]==1) c[v]=2;
if(c[v]!=2 && c[u]==0) c[v]=1;
}
for(int i=1;i<=n;i++)
if(c[i]==2) p[++k]=i;
printf("%d\n",k);
for(int i=1;i<=k;i++)
printf("%d ",p[i]);
puts("");
}
signed main()
{
T=read();
while(T--) work();
}
AGC032E Modulo Pairing
题目描述
解法
首先我们可以把 \((x+y)\bmod m\) 分为两类:\(x+y<m\) 和 \(x+y\geq m\)
那么如果只有第一类是好做的,从小到大排序之后把最大值和最小值匹配即可;如果只有第二类也是好做的,还是把最大值和最小值匹配;但是本题涉及两类匹配,就不是很好做了。
那么我们考虑融合这两种贪心方法,可以找到分界点 \(p\),使得 \(p\) 左边用第一种贪心,\(p\) 右边用第二种贪心。下图的蓝线表示一类匹配,红线表示二类匹配:
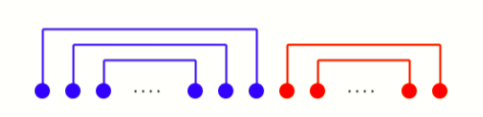
至于这种混合贪心的正确性可以考虑调整法:
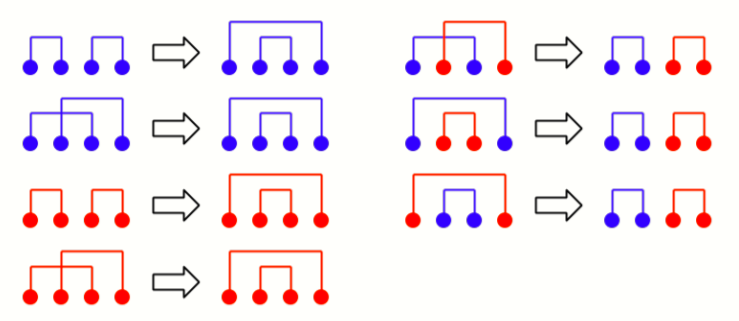
左边一列的调整是平凡的,右边一类的调整可以考虑:蓝色匹配的代价必然 \(\geq\) 右端点,红色匹配的代价必然 \(<\) 左端点,那么不难发现调整之后最大代价都是变小了的。
现在的问题变成如何找分界点了,不难发现分界点越靠左越好(证明考虑上面的代价不等式),但是太左了可能不满足红线匹配的条件,所以可以二分这个分界点,时间复杂度 \(O(n\log n)\)
总结
混合多种方法的思路十分重要:对于计数问题,混合不同的计数方法可能让需要记录的信息大大减少;对于贪心问题,混合贪心可以让局部最优,我们再考虑怎么从局部最优拓展到整体最优即可;对于图论问题(或者其他问题),混合方法在满足某一条件时快速解决,再满足另一条件时也能快速解决。
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 200005;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,a[M],ans;
int check(int p)
{
p<<=1;int r=0;
for(int i=1;i<=p/2;i++)
r=max(r,a[i]+a[p-i+1]);
for(int i=1;i<=(n-p)/2;i++)
{
int v=a[p+i]+a[n-i+1];
if(v<m) return 0;v-=m;
r=max(r,v);
}
ans=min(ans,r);
return 1;
}
signed main()
{
n=read()<<1;m=read();
for(int i=1;i<=n;i++) a[i]=read();
sort(a+1,a+1+n);
int l=0,r=n/2;ans=1e18;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1;
else l=mid+1;
}
printf("%lld\n",ans);
}
AGC028E High Elements
题目描述
解法
我们按位考虑,贪心地填 \(0\) 看是否可行,设 \(\{x\}\) 的前缀最大值 \(mx\),前缀最大值的次数是 \(cx\);设 \(\{y\}\) 的前缀最大值是 \(my\),前缀最大值的次数是 \(cy\),那么我们把问题转化成,找到子序列 \(\{a\}\),\(\{b\}\):
并且满足数量关系 \(cx+n_1=cy+n_2\),由于问题转化之后是子序列问题不是划分问题,所以我们还要添加限制:所有原序列前缀最大值(简称为大哥)都必须出现在子序列中,那么没有出现的元素就可以跟在大哥的后面,它们的影响就被消去了(彩蛋:我自己想这题的时候也是想到的最长上升子序列,只不过没有能力做出这么精妙的转化)
进一步考虑,因为我们只需要构造相等关系,所以可以使用调整法,让两边都去掉一个非大哥,这样相等关系还是成立。所以一定只有一边的子序列只含有大哥。
不妨设序列 \(\{a\}\) 只存在大哥,设现在还剩下 \(c\) 个大哥,序列 \(\{b\}\) 占了 \(k\) 个大哥,有 \(m\) 个非大哥,那么满足的关系式子是:\(cx+c-k=cy+k+m\),移项可得 \(cx+c-cy=2k+m\)
由于如果 \(k\) 存在,\(k-2\) 也一定存在(可以把一个大哥调整给对面),并且因为左边是定值,所以我们只需要分奇偶性维护右边的最大值即可,发现右边就是一个最长上升子序列,可以直接用线段树维护,时间复杂度 \(O(n\log n)\)
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 200005;
const int inf = 0x3f3f3f3f;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,a[M],w[M],mx[M<<2][2],cnt[M],ans[M];
void ins(int i,int l,int r,int id,int c,int f)
{
if(l==r) {mx[i][f]=c;return ;}
int mid=(l+r)>>1;
if(mid>=id) ins(i<<1,l,mid,id,c,f);
else ins(i<<1|1,mid+1,r,id,c,f);
mx[i][f]=max(mx[i<<1][f],mx[i<<1|1][f]);
}
int ask(int i,int l,int r,int L,int R,int f)
{
if(L>r || l>R) return -inf;
if(L<=l && r<=R) return mx[i][f];
int mid=(l+r)>>1;
return max(ask(i<<1,l,mid,L,R,f),
ask(i<<1|1,mid+1,r,L,R,f));
}
int check(int x,int w)
{
if(w<0) return 0;
if(w&1) return ask(1,1,n,x,n,1)>=w;
return ask(1,1,n,x,n,0)>=w;
}
signed main()
{
n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=0;i<=4*n;i++) mx[i][1]=-inf;
for(int i=1,mx=0;i<=n;i++)
{
if(a[i]>mx) w[i]=2,mx=a[i];
else w[i]=1;
}
for(int i=n;i>=1;i--)
{
int e=ask(1,1,n,a[i],n,0);//even
int o=ask(1,1,n,a[i],n,1);//odd
ins(1,1,n,a[i],(w[i]&1)?o+1:e+2,0);//even
ins(1,1,n,a[i],(w[i]&1)?e+1:o+2,1);//odd
}
for(int i=n;i>=1;i--) cnt[i]=cnt[i+1]+w[i]-1;
int mx=0,my=0,cx=0,cy=0;
for(int i=1;i<=n;i++)
{
ins(1,1,n,a[i],0,0);
ins(1,1,n,a[i],-inf,1);
if(check(my,cx+(a[i]>mx)-cy+cnt[i+1])
|| check(max(mx,a[i]),cy-cx-(a[i]>mx)+cnt[i+1]))
cx+=(a[i]>mx),mx=max(mx,a[i]);
else
cy+=(a[i]>my),my=max(my,a[i]),ans[i]=1;
}
if(cx!=cy) {puts("-1");return 0;}
for(int i=1;i<=n;i++) printf("%d",ans[i]);
puts("");
}



