#8 CF578E & CF578F & CF627E
Walking
题目描述
解法
首先考虑转化问题:我们可以把原序列划分成若干个 \(01\) 交替的子序列,然后再把 \(01\) 子序列交替拼起来,要求最小化 \(01\) 子序列的数量。
如果不考虑第二问,那么可以贪心地划分,假设现在要加入 \(1\),如果有结尾为 \(0\) 的子序列,那么直接插到它后面去,否则新开一个子序列(如果为 \(0\) 类似)
因为贪心求出的是一个较好的下界,我们考虑直接用贪心的结果构造。首先观察到 \(01\) 可以自身合并(以 \(0\) 开头 \(1\) 结尾的子序列),也就是若干个 \(01\) 拼起来结果还是 \(01\),\(10\) 也可以自身合并。
那么如果存在 \(11\) 或者 \(00\),如果 \(11\) 的数量更多,那么可以构造出 10 11 01 00 11 00... 这样的结果,这是因为 \(00\) 和 \(11\) 数量之差不超过 \(1\)(如果 \(00\) 的数量更多,或者数量相等都类似)
如果不存在 \(11\) 或者 \(00\),考虑调整出它们。如果全是 \(01/10\) 可以直接出解,否则我们可以那一组 \((01,10)\) 把他们调整成 \((00,11)\),只需要判断结尾位置的大小关系即可。
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 100005;
#define pb push_back
#define pp pop_back
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m;char s[M];vector<int> v[M],id[2],z[2][2];
void adjust()
{
if(!z[1][0].empty() || !z[1][0].empty()) return ;
if(z[0][0].empty() || z[0][1].empty()) return ;
int a=z[0][0].back(),b=z[0][1].back();
if(v[a].back()<v[b].back())
v[a].pb(v[b].back()),v[b].pp();
else v[b].pb(v[a].back()),v[a].pp();
z[0][0].pp();z[0][1].pp();
z[1][0].pb(b);z[1][1].pb(a);
}
void print(int x)
{
for(int i:v[x]) printf("%d ",i);
}
signed main()
{
scanf("%s",s+1),n=strlen(s+1);
for(int i=1;i<=n;i++)
{
int c=s[i]=='R';
if(id[c^1].empty()) id[c^1].pb(++m);
int t=id[c^1].back();
v[t].pb(i);id[c^1].pp();id[c].pb(t);
}
printf("%d\n",m-1);
for(int i=1;i<=m;i++)
z[v[i].size()&1][s[v[i].back()]=='R'].pb(i);
adjust();
int f=z[1][0].size()<z[1][1].size();
if(z[1][f].empty()) f=z[0][0].size()>z[0][1].size();
while(!z[0][f^1].empty())
print(z[0][f^1].back()),z[0][f^1].pp();
while(!z[1][f].empty())
{
print(z[1][f].back());z[1][f].pp();
while(!z[0][f].empty())
print(z[0][f].back()),z[0][f].pp();
f^=1;
}
}
Mirror Box
题目描述
解法
话说因为这题我私戳了djq,但是现在我还是不会结论的证明,以后再补吧。
考虑把问题转成在 \((n+1)\cdot (m+1)\) 的点阵中连边,可以发现合法方案对应黑点\(/\)白点的生成树。
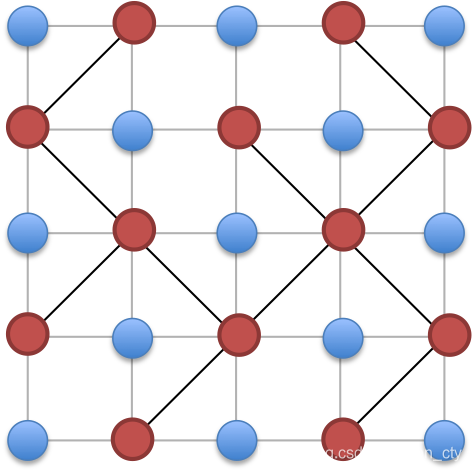
那么我们把 / 和 \ 对应的点用并查集连起来,然后对黑点白点分别跑矩阵树定理即可。
#include <cstdio>
#include <cstdlib>
#include <iostream>
using namespace std;
const int M = 505;
const int N = 200005;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,MOD,fa[N],num[N];char s[M][M];
int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
int id(int x,int y) {return (x-1)*(m+1)+y;}
int get(int x,int y) {return num[find(id(x,y))];}
void merge(int x,int y) {fa[find(x)]=find(y);}
int qkpow(int a,int b)
{
int r=1;
while(b>0)
{
if(b&1) r=r*a%MOD;
a=a*a%MOD;
b>>=1;
}
return r;
}
struct node
{
int n,a[M][M];
void add(int x,int y)
{
a[x][x]++;a[y][y]++;
a[x][y]--;a[y][x]--;
}
int gauss()
{
int ans=1;n--;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=(a[i][j]+MOD)%MOD;
for(int i=1;i<=n;i++)
{
for(int j=i;j<=n;j++)
if(!a[i][i] && a[j][i])
{
swap(a[i],a[j]);
ans*=-1;
break;
}
ans=ans*a[i][i]%MOD;
for(int j=1;j<=n;j++)
{
if(i==j || !a[j][i]) continue;
int t=a[j][i]*qkpow(a[i][i],MOD-2)%MOD;
for(int k=1;k<=n;k++)
a[j][k]=(a[j][k]-a[i][k]*t)%MOD;
}
}
return (ans+MOD)%MOD;
}
}G[2];
signed main()
{
n=read();m=read();MOD=read();
for(int i=1;i<=(n+1)*(m+1);i++) fa[i]=i;
for(int i=1;i<=n;i++)
{
scanf("%s",s[i]+1);
for(int j=1;j<=m;j++)
{
if(s[i][j]=='/')
merge(id(i+1,j),id(i,j+1));
if(s[i][j]=='\\')
merge(id(i,j),id(i+1,j+1));
}
}
for(int i=1;i<=n+1;i++)
for(int j=1;j<=m+1;j++)
if(id(i,j)==find(id(i,j)))
num[id(i,j)]=++G[(i+j)&1].n;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) if(s[i][j]=='*')
{
int f=(i+j)&1;
G[f].add(get(i,j),get(i+1,j+1));
G[!f].add(get(i+1,j),get(i,j+1));
}
printf("%lld\n",(G[0].gauss()+G[1].gauss())%MOD);
}
Orchestra
题目描述
解法
大致思路还是自己想出来的,因为我写不来所以细节参考了 大佬的博客。
首先我们可以考虑下一维问题怎么做,发现就是找到每个位置的 \(k\) 级后继,然后统计贡献即可,所以说如果我们枚举上下边界之后,可以套用一维的方法来做,复杂度 \(O(r^2c)\)
枚举太耗时间了,我们可以只枚举上边界,然后扫描下边界。由于 \(k\) 很小我们想把 \(k\) 放到复杂度里面去,考虑下边界从下往上移动的时候会导致一些点的删除,删除之后 \(k\) 级后继会变化,但是由于 \(k\) 很小,所以影响的点只会有 \(O(k)\) 个,这说明我们可以暴力修改这个后继。
具体实现采用双向链表(因为可以暴力跳,但是要求数据结构不带 \(\tt log\)),我们可以很容易地在双向链表上删除。对于每个点我们维护 \(cnt_i\) 表示 \(k\) 级前驱是 \(i\) 的位置 \(j\) 个数(注意这里的 \(j\) 是一个纵坐标),那么贡献显然是 \(\sum cnt_i\cdot y_i\),删除的时候 \(cnt\) 也很好维护,我们取出所有 \(k\) 级前驱,然后把这个点的 \(cnt\) 给到它的前驱即可。
时间复杂度 \(O(n^2k)\)(\(r,c,n\) 看做同阶)所以说这种方法其实还依赖于点数很小。
总结
矩形问题,有一种简单的思维方式是:先考察一维问题,再思考通过枚举把二维问题转化成一维问题,最后通过动态的方法优化枚举,虽然不是很巧妙但是常常都有作用。
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 3005;
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,c,k,x[M],y[M],a[M],L[M],R[M],cnt[M];
ll ans;vector<int> v[M];
int cmp(int a,int b) {return y[a]<y[b];}
void move(int x,int k)
{
if(!x || !k) return ;
move(L[x],k-1);
cnt[L[x]]+=cnt[x];cnt[x]=0;
}
void work(int l)
{
int t=0;ll sum=0;
for(int i=0;i<=c;i++) a[i]=L[i]=R[i]=cnt[i]=0;
for(int i=1;i<=c;i++)//get all the point
if(x[i]>=l) a[++t]=i;
sort(a+1,a+1+t,cmp);//sort in the order of y
//initialize the chain table
for(int i=1;i<=t;i++) L[a[i]]=a[i-1],R[a[i]]=a[i+1];
//calc the initial cnt
for(int i=1,j=0;i<=m;i++)
{
while(j<t && y[a[j+1]]==i) j++;
int p=a[j];
for(int o=1;o<k;o++) p=L[p];
cnt[p]++;
}
for(int i=1;i<=t;i++) sum+=cnt[a[i]]*y[a[i]];
ans+=sum;
//iterate the lower bound
for(int r=n;r>l;r--)
{
for(int x:v[r])//delete them
{
int p=x;
for(int i=1;i<=k;i++)
{
sum-=cnt[p]*(y[p]-y[L[p]]);
p=L[p];if(!p) break;
}
move(x,k);L[R[x]]=L[x];R[L[x]]=R[x];
}
ans+=sum;
}
}
signed main()
{
n=read();m=read();c=read();k=read();
for(int i=1;i<=c;i++)
x[i]=read(),y[i]=read(),v[x[i]].push_back(i);
for(int i=1;i<=n;i++) work(i);
printf("%lld\n",ans);
}




