AtCoder Grand Contest 013&014
013D Piling Up
题目描述
解法
还是把一开始的球确定了好 \(dp\),否则写出来的 \(dp\) 奇奇怪怪还不好优化。
枚举初始时有 \(x\) 个白球 \(n-x\) 个黑球,注意每一轮之后球数都是 \(n\),可以设 \(dp[i][j]\) 表示前 \(i\) 轮过后有 \(j\) 个白球对应序列方案数,我们考虑这一轮放置的方法可以得到这样的转移:
- 若 \(j\geq1\),先放置白球:\(dp[i][j-1]\leftarrow dp[i-1][j]\),\(dp[i][j]\leftarrow dp[i-1][j]\)
- 若 \(j<n\),先放置黑球:\(dp[i][j+1]\leftarrow dp[i-1][j]\),\(dp[i][j]\leftarrow dp[i-1][j]\)
其实我们不需要枚举,由于转移方式都是相同的,我们做整体 \(dp\) 就行了(本题体现为多点初始化)
但是这样会算重,考虑两种不同的初始状态可能对应着相同的序列,但是放在坐标上是同构的:
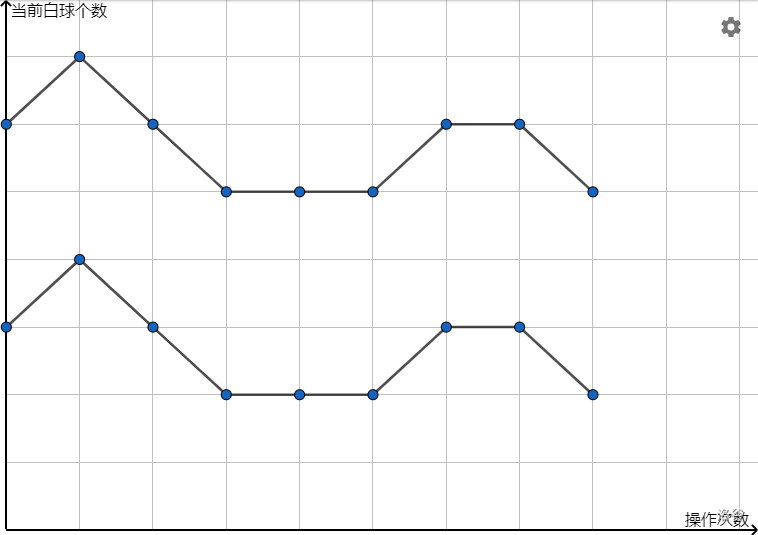
所以我们强制路径碰到 \(j=0\) 就可以不算重了,这只需要在状态中增加一维。
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 3005;
const int MOD = 1e9+7;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,w,ans,f[2][M][2];
void add(int &x,int y) {x=(x+y)%MOD;}
void work()
{
w^=1;memset(f[w],0,sizeof f[w]);
for(int j=0;j<=n;j++)
{
int a=f[w^1][j][0],b=f[w^1][j][1];
if(j>=1)
{
//bb
if(j==1) add(f[w][j-1][1],a);
else add(f[w][j-1][0],a);
add(f[w][j-1][1],b);
//bw
if(j==1) add(f[w][j][1],a);
else add(f[w][j][0],a);
add(f[w][j][1],b);
}
if(j<n)
{
//ww
add(f[w][j+1][0],a);
add(f[w][j+1][1],b);
//wb
add(f[w][j][0],a);
add(f[w][j][1],b);
}
}
}
signed main()
{
n=read();m=read();
f[0][0][1]=1;
for(int i=1;i<=n;i++) f[0][i][0]=1;
for(int i=1;i<=m;i++) work();
for(int i=0;i<=n;i++) add(ans,f[w][i][1]);
printf("%d\n",ans);
}
013F Two Faced Cards
题目描述
解法
先考虑一个简化的问题,如果 \(q=1\) 怎么做?
大方向肯定是 \(\tt Hall\) 定理,平凡的转化是:我们把 \(A,B\) 都按照 \(C\) 离散化(\(n\leftarrow n+1\) 之后,直接 \(\tt lower\_bound\))后,\(A/B\) 对应着后缀加,\(C\) 对应着后缀减,假设得到的数组为 \(s\),要求是 \(\forall i,s_i\geq 0\)
可以考虑调整法来获得最优的结果,我们一开始强制所有都选 \(A\),然后得到 \(s\),若 \(b_i<a_i\),那么我们可以花费 \(1\) 的代价使得 \([b_i,a_i)\) 这个区间的 \(s\) 增加 \(1\),考试时我以为这是不可做的,但是这其实是一个简单的区间贪心问题。
考虑把得到的区间按照右端点排序,然后从右往左覆盖,如果当前点的 \(s_i<0\),那么就选取一个左端点最左的区间,如果不存在这样的区间自然无解,这个过程可以用优先队列维护。
现在考虑多组询问,由于询问的影响是微弱的(虽然在答案上大相径庭,但是只造成了单点的影响),我们可以考虑对于每个 \(x\) 求出,强制选 \(x\) 需要花费的代价。
考虑强制选 \(x\) 会让 \(s[x\sim n]\) 这些区间加上 \(1\),所以我们还是从右到左覆盖,使得 \(s_i\geq -1\)
然后从左到右考虑,如果 \(s_i=-1\) 那么证明当 \(x\geq i+1\) 时,\(i\) 还是需要覆盖的,我们可以找出第一次覆盖还没有使用过的区间,来做第二次覆盖,这里我们选取右端点最靠右的区间即可。
时间复杂度 \(O(n\log n)\)
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int M = 100005;
#define pii pair<int,int>
#define pb push_back
#define x first
#define y second
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,a[M],b[M],c[M],s[M],ad[M],ans[M],use[M];
priority_queue<pii> q;vector<int> v[M];
void lisan(int &x) {x=lower_bound(c+1,c+1+n,x)-c;}
signed main()
{
n=read()+1;
for(int i=1;i<n;i++) a[i]=read(),b[i]=read();
for(int i=1;i<=n;i++) c[i]=read();
sort(c+1,c+1+n);m=read();
for(int i=1;i<n;i++) lisan(a[i]),lisan(b[i]);
for(int i=1;i<n;i++) s[a[i]]++;
for(int i=1;i<=n;i++) s[i]+=s[i-1]-1;
//intervals
for(int i=1;i<n;i++)
{
if(a[i]>b[i]) v[a[i]-1].pb(i);
else use[i]=1;
}
//cover I
for(int i=n,nw=0;i>=1;i--)
{
for(int x:v[i]) q.push({-b[x],x});
nw+=ad[i];
while(s[i]+nw<-1)
{
while(!q.empty() && -q.top().x>i) q.pop();
if(q.empty()) {while(m--)puts("-1");return 0;}
int x=q.top().y;q.pop();
use[x]=1;ans[1]++;
nw++;ad[a[x]-1]++;ad[b[x]-1]--;
}
}
while(!q.empty()) q.pop();
for(int i=n;i>=1;i--) s[i]+=(ad[i]+=ad[i+1]);
//cover II
for(int i=1;i<=n;i++) v[i].clear(),ad[i]=0;
for(int i=1;i<n;i++) if(!use[i]) v[b[i]].pb(i);
for(int i=1,nw=0;i<=n;i++)
{
for(int x:v[i]) q.push({a[x],x});
ans[i+1]=ans[i];nw+=ad[i];
while(s[i]+nw==-1)
{
while(!q.empty() && q.top().x<i) q.pop();
if(q.empty())
{
for(int j=i+1;j<=n+1;j++) ans[j]=n+1;
goto yhpyyds;
}
int x=q.top().y;q.pop();
ans[i+1]++;nw++;
ad[b[x]]++;ad[a[x]]--;
}
}
yhpyyds:;
while(m--)
{
int u=read(),v=read(),zxy=-1;
lisan(u);lisan(v);
zxy=max(zxy,n-ans[u]);
zxy=max(zxy,n-ans[v]-1);
printf("%d\n",zxy);
}
}



