[省选集训2022] 模拟赛12
高维游走
题目描述
考虑以下在 \(m\) 维空间的游走过程:初始时你在原点,即每一维坐标为 \(0\) 的位置。接下来依次有 \(\sum_{i=0}^m t_i\) 次操作,分为 \(m+1\) 个阶段。第 \(0\) 个阶段有 \(t_0\) 次操作,每次操作可以不动或者选择任意一维向其正方向前进 \(1\) 个单位长度。第 \(i(1\leq i\leq m)\) 个阶段有 \(t_i\) 次操作,每次操作可以不动或者提升 \(i\) 点疲倦度的同时向第 \(i\) 维负方向前进 \(1\) 个单位长度。
设 \(f(x)\) 表示所有操作结束后回到游走起点的方案中疲劳度为 \(x\) 的方案数,定义两个方案不同当且仅当某一次操作的决策不同。你需要求 \(\sum_{i=0}^{\infty}\{f_i\bmod2\}\) 的值。
多组数据:\(1\leq T\leq 200\),\(1\leq m\leq 10,1\leq t_i<2^{31}\)
解法
设 \(x_i\) 表示最终向第 \(i\) 维走了 \(x_i\) 步,那么它对应的方案数是:
那么贡献为 \(1\) 的充要条件是:\(t_i\and x_i=x_i\),\(\{x\}\) 是 \(t_0\) 二进制位的拆分。后面的性质可以用归纳法证明,首先要满足 \(t_0\and x_1=x_1\),那么 \(x_1\) 相当于把 \(t_0\) 的二进制位拆了一些出来,\(x_2\) 继续拆分 \(t_0-x_1\),那么就可以证明了。
那么我们考虑规划合法的 \(\{x\}\),不同的方案以疲劳度来区分。考虑疲劳度是 \(\sum_{i=1}^m x_i\cdot i\),那么我们依次考虑 \(t_0\) 的每个二进制位,再决策这一位分配给 \(x\) 的 \(0\sim m\) 的哪一个即可(如果分配 \(0\) 代表这一位不选),对于以前的位都相同的方案,我们在第一个导致数位不同的地方它们区分出来。
设 \(dp[i][s]\) 表示考虑前 \(i\) 位,进位到 \(2^{i+1}\) 的集合是 \(s\)(如果 \(s_j=1\) 代表进位得到 \(j\cdot 2^{i+1}\) 是可行的)的方案数,那么转移考虑枚举 \(t_0\) 第 \(i\) 位要分配给 \(0\sim m\) 中的哪一个。注意两种方案如果此后进位还是相同那么需要抵消,所以我们可以维护两个集合 \(s_1,s_2\),表示第 \(i\) 位疲劳值是 \(1/0\) 转移到的状态,用异或的方式来抵消即可。
时间复杂度 \(O(T\cdot 2^{m}\cdot m^2\cdot \log t)\)
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 50;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int T,n,m,t[M],vis[M],mp[M][M],dp[M][1<<10];
void work()
{
memset(vis,0,sizeof vis);
memset(mp,0,sizeof mp);
memset(dp,0,sizeof dp);
m=read();
for(int i=0;i<=m;i++) t[i]=read();
for(int i=1;i<=m;i++)
{
n=0;
while(t[i]) mp[n++][i]=t[i]&1,t[i]>>=1;
}
n=0;while(t[0]) vis[n++]=t[0]&1,t[0]>>=1;
for(int i=0;i<n;i++) mp[i][0]=1;
int w=0,ans=0,lim=(1<<10);
dp[0][1]=1;
for(int i=0;i<n;i++)
{
w^=1;memset(dp[w],0,sizeof dp[w]);
int up=vis[i]?m:0;
for(int j=0;j<lim;j++)
{
int s1=0,s2=0;
for(int k=0;k<10;k++) if(j>>k&1)
for(int l=0;l<=up;l++) if(mp[i][l])
{
if(k+l&1) s1^=(1<<(k+l>>1));
else s2^=(1<<(k+l>>1));
}
dp[w][s1]+=dp[w^1][j];
dp[w][s2]+=dp[w^1][j];
}
}
for(int i=0;i<lim;i++)
for(int j=0;j<10;j++)
if(i>>j&1) ans+=dp[w][i];
printf("%lld\n",ans);
}
signed main()
{
freopen("travel.in","r",stdin);
freopen("travel.out","w",stdout);
T=read();
while(T--) work();
}
过山车
题目描述
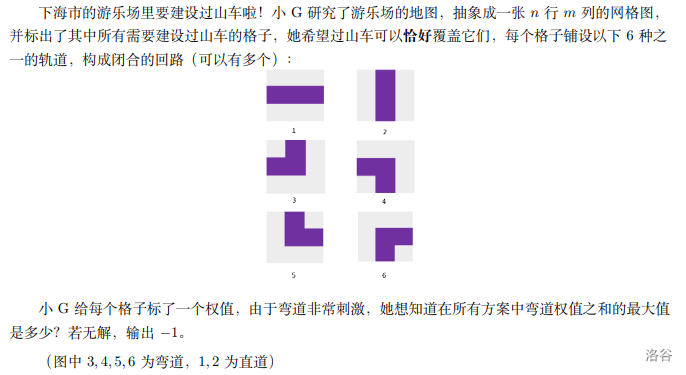
\(1\leq n\leq 150,1\leq m\leq 30,0\leq w[i][j]\leq 100\)
解法
考虑最后答案的形式:若干个哈密顿圈,转角的点会产生贡献。
显然哈密顿圈是 \(\tt np\) 问题,但因为这是平面图,所以关键性质是它可以黑白染色。
那么我们把平面图黑白染色,尝试转化为二分图问题。首先考虑如何判定,可以给每个需要覆盖的点(下文称之为关键点) \(2\) 的流量,如果两个关键点相邻那么连一条流量为 \(1\) 的边,对它跑网络流,满流是有解的充要条件。
那么我们考虑魔改上面的图来完成最大化权值的目的,注意到弯道是竖直方向和水平方向的拼接,那么我们可以考虑拆点,对于每个 \(x\) 我们再新建 \(x_1,x_2\) 表示竖直点和水平点,那么我们在同时选取竖直点和水平点的时候计算贡献:
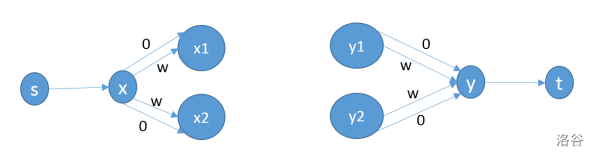
上图展示了建图的一部分,另一部分是:如果 \(x,y\) 竖直相连,那么把 \(x_1,y_1\) 连一条流量为 \(1\) 的边;如果 \(x,y\) 水平相连,那么把 \(x_2,y_2\) 连一条流量为 \(1\) 的边。然后我们对这个图跑最小费用流,再用总权值去减就可以得到答案。因为如果同时使用 \(x_1,x_2\) 得到的权值是 \(0\) 最后的贡献就是 \(w\),如果只使用一边那么最后的贡献是 \(0\)
好像这题只有 \(\tt spfa\) 才能通过 \(...\)
#include <cstdio>
#include <iostream>
#include <queue>
using namespace std;
const int M = 20005;
const int inf = 0x3f3f3f3f;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,a[155][35],b[155][35],id[155][35][3];
int tot,S,T,ans,f[M],dis[M],flow[M],pre[M],lst[M];
int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
struct edge{int v,f,c,next;}e[M*100];
void add(int u,int v,int F,int c)
{
e[++tot]=edge{v,F,c,f[u]},f[u]=tot;
e[++tot]=edge{u,0,-c,f[v]},f[v]=tot;
}
int bfs()
{
queue<int> q;
for(int i=S;i<=T;i++)
dis[i]=inf,flow[i]=pre[i]=lst[i]=0;
dis[S]=0;flow[S]=inf;q.push(S);
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v,c=e[i].c;
if(dis[v]>dis[u]+c && e[i].f>0)
{
dis[v]=dis[u]+c;
flow[v]=min(flow[u],e[i].f);
pre[v]=u;lst[v]=i;
q.push(v);
}
}
}
return flow[T]>0;
}
signed main()
{
freopen("roller.in","r",stdin);
freopen("roller.out","w",stdout);
n=read();m=read();
//initialize
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
a[i][j]=read();
if(!a[i][j]) for(int k=0;k<3;k++)
id[i][j][k]=++T;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
b[i][j]=read();
int A=0,B=0,sum=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(i+j&1) A+=(!a[i][j]);
else B+=(!a[i][j]);
}
if(A!=B) {puts("-1");return 0;}
S=0;T++;tot=1;
//build the graph
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) if(i+j&1)
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x<1 || y<1 || x>n || y>m) continue;
if(a[i][j]+a[x][y]) continue;
add(id[i][j][k%2],id[x][y][k%2],1,0);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) if(!a[i][j])
{
int x=id[i][j][2],w=b[i][j];ans+=w;
if(i+j&1)
{
sum+=2;
add(S,x,2,0);
add(x,id[i][j][0],1,0);
add(x,id[i][j][0],1,w);
add(x,id[i][j][1],1,0);
add(x,id[i][j][1],1,w);
}
else
{
add(x,T,2,0);
add(id[i][j][0],x,1,0);
add(id[i][j][0],x,1,w);
add(id[i][j][1],x,1,0);
add(id[i][j][1],x,1,w);
}
}
while(bfs())
{
sum-=flow[T];
ans-=flow[T]*dis[T];
int u=T;
while(u!=S)
{
e[lst[u]].f-=flow[T];
e[lst[u]^1].f+=flow[T];
u=pre[u];
}
}
if(sum) {puts("-1");return 0;}
printf("%lld\n",ans);
}
木棍
题目描述
有 \(n\) 根木棍,所有木棍的长度都为 \(k\),现在要把木棍排列到数轴上,第 \(i\) 个木棍的左端点 \(\geq a_i\),右端点 \(\leq b_i\),并且要求任意两个木棍之间不能有公共长度(但是可以点交)
此外还有 \(m\) 个限制,第 \(i\) 条形如: 左端点大于等于 \(x_i\),右端点小于等于 \(y_i\) 的木棍至多有 \(c_i\) 条。问是否存在解,注意只需要回答存不存在,而不需要构造解。
\(n\leq 1000,m\leq 1000,k\leq 10^9\)
解法
首先把限制都转成左端点的限制,只需要把右端点减去 \(k\) 即可。
如果不考虑 \(m\) 个限制并且 \(k=1\),那么剩下的限制就是每个木棍的可放置范围是一个区间,那么显然可以木棍到点连出一个二分图,然后跑网络流判断是否有解。当然可扩展的方式是使用 \(\tt Hall\) 定理,我们可以把所有端点离散化,那么只保留区间的限制就是充分的。
限制形如这段区间的木棍数量 \(\geq x\),可以用差分约束来表示限制,设 \(s_i\) 表示前缀 \(i\) 放置的木棍个数,那么 \(s_r-s_{l-1}\geq x\)
发现 \(k\not=1\) 也是可以考虑的,也就是 \(s_{i+k}-s_i\leq 1\),那么离散化后就是 \(s_{a_i}-s_{a_{i-1}}\leq\lceil\frac{a_i-a_{i-1}}{k}\rceil\);\(m\) 的限制同样是可以考虑的,就是 \(s_{y_i}-s_{x_i-1}\leq c_i\);最后由于合法还需要添加一类边:就是 \(s_i-s_{i-1}\geq 0\)
然后暴力 \(\tt spfa\) 即可(如果时间用完了直接无解),注意离散化时我们要把左端点 \(-1\) 丢进去。




