[省选集训2022] 模拟赛10
遇到困难睡大觉
题目描述
给定 \(n\) 个元素,每个元素有两个属性值 \((a_i,b_i)\),我们可以将其以任意顺序排列,要最大化下式:
\(n\leq 10^5,a_i,b_i,kn\leq 10^9\)
解法
应该是遇到困难退大火才对,直接使用枚举法,考虑枚举 \(m=\min(a_i+i\cdot k)\),那么为了满足这个 \(m\) 的限制,第 \(i\) 个元素的位置必须 \(\geq \lceil\frac{m-a_i}{k}\rceil\),我们记这个临界值是 \(c_i\),那么知道所有元素的 \(c_i\) 我们直接贪心,按照 \(b\) 下降的顺序把数尽量的往前放,正确性有两点:合法性一定能保证;用调整法可以证明 \(b\) 大的不必给后面留出前面的位置。
现在的问题在于确定这个 \(m\)(直接退火肯定是不行的),我们考虑确定它的大致范围,首先我们把 \(a\) 从大到小排序,按照这个顺序可以计算 \(m\) 的最大值 \(mx\),结论是 \(m\) 的取值一定在 \((mx-k,mx]\) 中。
证明可以考虑调整法,考虑我们把 \(m\) 调大 \(k\) 之后任然 \(\leq mx\),那么此时我们考虑 \(\max(b_i+i\cdot k)\) 的变化即可,由于调大之后 \(c_i\) 都增加 \(1\),最坏情况是把所有位置向右平移(而且不可能实现),所以它至多增加 \(k\)
那么有这个较精确的范围就可以退火了。说一下细节:我们以 \(m\) 为退火的起点,每次就给一个 \([0,k)\) 中的数增加一个和温度 \([-T,T]\) 中的随机向量,然后卡准秒数退火即可,注意 \(D\) 设置为 \(0.98\) 较优秀(降温速度较快)
UPD:据说本题是论文题,待我看懂论文以后再把正确做法给补上来。
总结
退火其实是很有讲究的,并不是一个模板可以走天下,下面就来谈一谈我的心得感悟:
- 退一个排列的方法虽然看起来很牛,但是一定要保证有答案的浮动(一直都是一个值那怎么退?),并且计算函数一定要保证绝对正确,\(n\) 最多是几百的数量级,更大的就不要妄想了。
- 更好的退火是退一个阈值\(/\)退一个坐标,这样对所有情况的考虑会更充分,你可以把它当成没有单调性的分治来使用。这种连续型退火注意要让步长和温度正相关。
- 计算函数应该对答案具有更大的包容性,如本题应该在 \(b\) 相同的情况 \(a\) 大的放前面,最后不以 \(m\) 当成最小值而是以当前局面的 \(a\) 去计算,这样得到的"最小值"可能会大一些。
- 最后退火是需要脑子的,建立在更多结论和人类智慧的退火更强大。
#include <cstdio>
#include <cassert>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <ctime>
using namespace std;
const int M = 100005;
const int inf = 2e9;
#define db double
const db D = 0.98;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,k,mx,ans,c[M],d[M],fa[M];
struct node
{
int a,b;
bool operator < (const node &r) const
{return (b==r.b)?a>r.a:b>r.b;}
}s[M];
int random(int x) {return (rand()*rand()+rand())%x;}
int Random(int l,int r) {return l+random(r-l+1);}
int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];
}
int calc(int m)
{
for(int i=1;i<=n+1;i++) fa[i]=i;
for(int i=1;i<=n;i++)
c[i]=max(1,(m-s[i].a+k-1)/k);
for(int i=1;i<=n;i++)
{
int t=find(c[i]);
d[t]=i;fa[t]=find(t+1);
}
int mx=0,mi=inf;
for(int i=1;i<=n;i++)
{
mi=min(mi,s[d[i]].a+i*k);
mx=max(mx,s[d[i]].b+i*k);
}
return mi-mx;
}
void zxy()
{
db T=1e9;int p=0;ans=max(ans,calc(0));
while(T>1 && 1.0*clock()/CLOCKS_PER_SEC<=2.95)
{
int np=(p+Random(-T,T)%k+k)%k;
int tmp=calc(mx-np),d=tmp-ans;
if(d>0) ans=tmp,p=np;
else if(exp(d/T)*RAND_MAX>=rand()) p=np;
T*=D;
}
}
signed main()
{
freopen("sleep.in","r",stdin);
freopen("sleep.out","w",stdout);
n=read();k=read();srand(time(0));
for(int i=1;i<=n;i++)
s[i].b=read(),s[i].a=c[i]=read();
sort(s+1,s+1+n);
sort(c+1,c+1+n);
mx=inf;ans=-inf;
for(int i=1;i<=n;i++)
mx=min(mx,c[i]+(n-i+1)*k);
while(1.0*clock()/CLOCKS_PER_SEC<=2.95) zxy();
printf("%d\n",ans);
}
麻烦的杂货店
题目描述
给定一个长度为 \(n\) 个括号序列,现在有 \(m\) 次询问,每次询问 \([l,r]\) 之间最长的合法括号序列长度。
\(n\leq 10^5,m\leq 4\cdot 10^6\)
解法
显然可以转化成前缀和的形式,我们令 ( 为 \(-1\),) 为 \(1\) 求出其前缀和 \(a_i\),那么合法括号序列 \([l,r]\) 的充要条件是:\(\forall i\in[l,r],a_i\leq a_{l-1},a_r=a_{l-1}\)
这个条件还是不够简洁,可以进一步转化,我们考虑充分利用 \(|a_i-a_{i-1}|=1\) 的性质,把前缀和在二维平面上描点(我们在第一个位置插入一个 \(0\) 点,所以横坐标范围是 \(n+1\))
考虑某点为合法括号序列右端点,那么最远的左端点就是左边第一个比它大的点的位置 \(+1\);考虑某点为合法括号序列左端点,那么最远的右端点就是右边第一个比它大的点的位置 \(-1\)
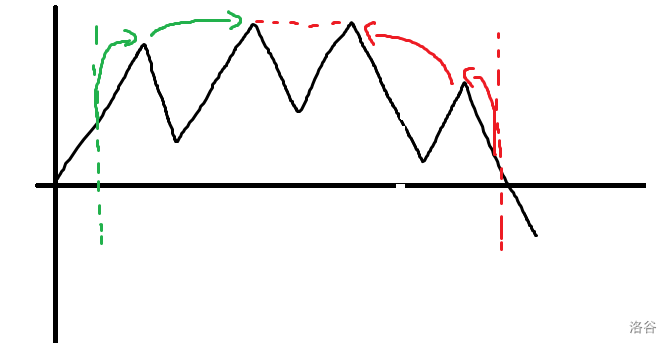
上图展示了我们如何处理单次询问,可以左右端点往中间跳,每次跳到第一个比它大的点,然后计算贡献;最后还可能跳到等高的位置,也需要计算贡献。
那么用单调栈预处理出左右第一个比它大的位置之后,就可以用倍增解决这道题了,时间复杂度 \(O(m\log n)\)
总结
使用倍增法的重要步骤是结合单次询问分析,而不是考虑合法段对询问的贡献。
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 100005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
void write(int x)
{
if(x>=10) write(x/10);
putchar(x%10+'0');
}
int n,m,k,a[M],p[M];char s[M];
int l[M][20],r[M][20],ml[M][20],mr[M][20];
signed main()
{
freopen("grocery.in","r",stdin);
freopen("grocery.out","w",stdout);
n=read();m=read();scanf("%s",s+1);
for(int i=1;i<=n;i++)
{
a[i+1]=a[i];
if(s[i]=='F') a[i+1]--;
else a[i+1]++;
}
n++;p[k=1]=1;
for(int i=2;i<=n;i++)
{
while(k && a[p[k]]<=a[i]) k--;
l[i][0]=k?p[k]:0;
ml[i][0]=i-p[k]-1;
p[++k]=i;
}
p[k=1]=n;
for(int i=n-1;i>=1;i--)
{
while(k && a[p[k]]<=a[i]) k--;
r[i][0]=k?p[k]:0;
mr[i][0]=p[k]-i-1;
p[++k]=i;
}
for(int j=1;j<=19;j++)
for(int i=1;i<=n;i++)
{
l[i][j]=l[l[i][j-1]][j-1];
r[i][j]=r[r[i][j-1]][j-1];
ml[i][j]=max(ml[i][j-1],ml[l[i][j-1]][j-1]);
mr[i][j]=max(mr[i][j-1],mr[r[i][j-1]][j-1]);
}
while(m--)
{
int a=read(),b=read()+1,ans=0;
for(int i=19;i>=0;i--)
{
if(r[a][i]>=a && r[a][i]<=b)
ans=max(ans,mr[a][i]),a=r[a][i];
if(l[b][i]>=a && l[b][i]<=b)
ans=max(ans,ml[b][i]),b=l[b][i];
}
ans=max(ans,b-a);
write(ans),puts("");
}
}
钥匙
题目描述
有 \(m\) 个位置,每个位置的钥匙数 \(\leq a_i\),选择每个位置的概率是 \(p_i\),给定 \(d\),保证 \(d|(a_i+1)\)
一共有 \(n\) 把钥匙,对于每种可能的局面,你需要计算钥匙数 \(\geq k\) 的概率之和,模 \(998244353\)
\(m\leq 100,k\leq n\leq \sum a_i,n\leq 100d,d|(a_i+1)\)
解法
本题把复杂度降下来的关键条件是 \(n\leq 100d\) 和 \(d|(a_i+1)\),考虑 \(a_i+1\) 这个东西的意义我们是熟悉的,对于计算总方案我们考虑容斥的话,那么强制一个位置放 \(a_i+1\) 把钥匙得到 \(-1\) 的容斥系数。
那么本题我们把概率放在容斥 \(dp\) 中,重要的还是分步思想,因为选择哪些位置和位置贡献的钥匙是互不干扰的,我们可以先决策选择哪些位置然后再往位置里面放钥匙,所以可以设计 \(dp[n_1][n_2][m_1]\) 表示不合法的钥匙选择 \(n_1\cdot d\),未选择 \(n_2\cdot d\),一共有 \(m_1\) 个位置被选择,那么转移我们需要决策这个位置合不合法\(/\)选不选择,所以是个 \(2\times 2\) 的转移。
那么处理完这个 \(dp\) 之后,我们考虑处理这样的问题,一共有 \(n_1+n_2\) 把钥匙,有 \(m_1+m_2\) 个位置,把钥匙任意放在位置上,要求前 \(m_1\) 个位置至少有 \(n_1\) 把钥匙,其中 \(n_1=k-n_1'\cdot d,n_2=n-k-n_2'\cdot d\),那么我们可以枚举第 \(n_1\) 把钥匙的位置,它的位置在 \(m_1\) 以前就等价于前 \(m_1\) 个位置有 \(n_1\) 把钥匙(因为我们需要 \(O(m)\) 的复杂度):
那么总时间复杂度 \(O(m^2(\frac{n}{d})^2)\)
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 105;
const int MOD = 998244353;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,d,k,w,ans,a[M],p[M],inv[M],f[2][M][M][M];
void add(int &x,int y) {x=(x+y)%MOD;}
int C(int n,int m)
{
if(m<0 || n<m) return 0;
int r=1;
for(int i=n;i>n-m;i--) r=r*i%MOD;
for(int i=1;i<=m;i++) r=r*inv[i]%MOD;
return r;
}
void init()
{
inv[0]=inv[1]=w=f[0][0][0][0]=1;
for(int i=2;i<=m;i++)
inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
for(int i=1;i<=m;w^=1,i++) for(int x=0;x<=n/d;x++)
for(int y=0;y<=n/d;y++) for(int k=0;k<=i;k++)
{
int &t=f[w][x][y][k],op=1-p[i];t=0;
//legal and not choose
add(t,f[w^1][x][y][k]*op);
//legal and choose
if(k) add(t,f[w^1][x][y][k-1]*p[i]);
//illegal and not choose
if(y>=a[i]) add(t,-f[w^1][x][y-a[i]][k]*op);
//illegal and choose
if(k && x>=a[i])
add(t,-f[w^1][x-a[i]][y][k-1]*p[i]);
}
w^=1;
}
void calc()
{
int tmp[M]={},res=0,c=0;
for(int x=0;x<=n/d;x++) for(int y=0;y<=n/d;y++)
for(int m1=1;m1<=m;m1++)//the number of the choosen
{
int p=f[w][x][y][m1];if(!p) continue;
int n1=k-d*x,n2=n-k-d*y;
if(n2<0 || n1+n2<0) continue;
if(n1<=0)//the constraints are already handled
{
int s=n-d*(x+y);
add(ans,p*C(s+m-1,m-1));
continue;
}
tmp[0]=c=1;res=0;
for(int i=1;i<=m;i++)//C(n2+i,n2)
tmp[i]=tmp[i-1]*(n2+i)%MOD*inv[i]%MOD;
for(int i=1;i<=m1;i++)//c=C(n1-1+i-1,n1-1)
{
add(res,c*tmp[m-i]);
c=c*(n1-1+i)%MOD*inv[i]%MOD;
}
add(ans,p*res);
}
}
signed main()
{
freopen("key.in","r",stdin);
freopen("key.out","w",stdout);
m=read();d=read();n=read();k=read();
for(int i=1;i<=m;i++)
a[i]=(read()+1)/d,p[i]=read();
init();calc();
printf("%lld\n",(ans+MOD)%MOD);
}



