[做题笔记] 2-sat 问题的进阶应用
对称性
考虑 \(\tt 2sat\) 边的意义是：如果选取了 \(i\) 则必须选取 \(j\)，那么如果我们连边 \((i,j)\)，我们都是也需要连边 \((inv(j),inv(i))\)（\(inv(x)\) 即表示变量 \(x\) 的逆），因为原命题和其逆否命题真假相同。
那么发现这样建出来的图具有某种对称性，此性质是 \(\tt 2sat\) 算法最重要的性质。
解的构造
设 \(col_i\) 表示 \(i\) 所在强连通分量的拓扑序编号（编号小的拓扑序大），那么如果 \(col_i<col_{i+n}\) 我们选取 \(i\)；否则我们选取 \(i+n\)
要证明上述构造是正确的，我们只需要证明被选取点不能到达没有未被选取的点。使用反证法，假设存在被选取点 \(x\) 和未被选取 \(y\)，并且存在 \(x\rightarrow y\) 的路径，那么显然有 \(col_x\geq col_y\)，同时根据对称性，存在一条 \(inv(y)\rightarrow inv(x)\) 的路径，所以有 \(col_{y+n}\geq col_{x+n}\)
根据选取的关系可以知道：\(col_x<col_{x+n},col_{y}>col_{y+n}\)，所以可以推出 \(col_{x+n}>col_x\geq col_y>col_{y+n}\)，但是这与 \(col_{y+n}>col_{x+n}\) 矛盾，反证法证毕。
特殊的边
这里有一个小 \(\tt trick\)：如果 \(i\) 强制不能选取，那么可以连一条 \((i,inv(i))\) 的边，表示强制不能选 \(i\)
这样连边还是满足对称性，用处很多：NOI2017 游戏
字典序最小的解
这种问题建议用直接 \(\tt dfs\) 的方法，也就是先搜字典序小的再搜索字典序大的。
这个问题也是可拓展的，既然是字典序问题就很容易和贪心产生联系：New Language
前后缀优化建图
本质思想还是建虚点来优化建图，连向这个虚点就代表了连向一个前缀\(/\)后缀。
如果你遇到要连向除一个点之外所有点的问题，那么可以拆成前缀与后缀的连边：Duff in Mafia
Ants (树链剖分优化建图)
题目描述
解法
我们把路径当成点建 \(\tt 2sat\)，每只蚂蚁的两条路径互为逆元。那么如果两条路径 \((x,y)\) 有交，那么可以连接 \((x,inv(y))\) 和 \((y,inv(x))\)，有一个建图的小技巧是把 \((x,y)\) 当成无序对，然后把这两条边一次性连好。
我们先把这些路径通过树链剖分放在线段树上，那么我们现在想完成的功能是：把某点和子树中的所有其他点连边。注意这里不要被传统的线段树优化建图束缚住了，这里我们可以魔改经典的前后缀优化建图的思想：
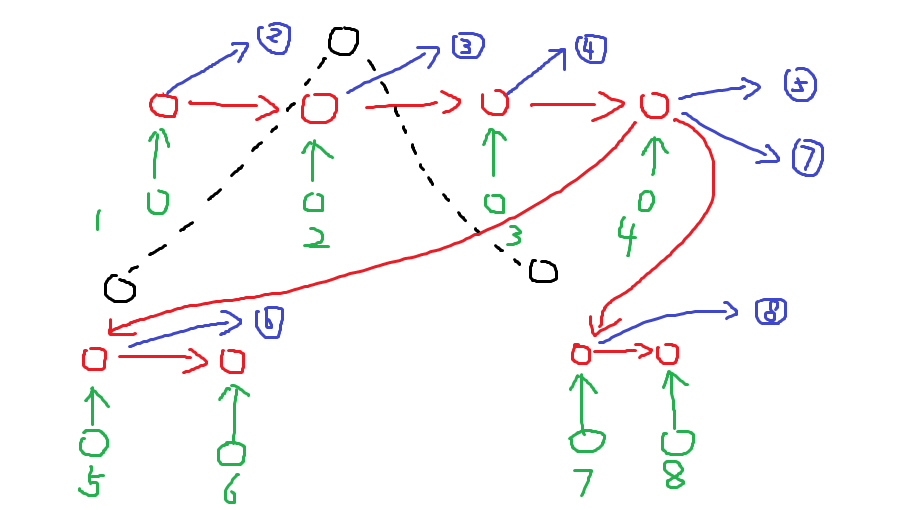
其中黑色点代表原线段树上的节点；红色点代表这一层建出的虚点，点数和节点的路径数量一致；绿色点表示节点的路径；蓝色点表示路径的逆。上述建图方法的主体还是前后缀优化建图，只是为了连到子树内，把上一层的最后一个虚点当成这一层的第一个虚点，时间复杂度 \(O(m\log n^2)\)
#include <cstdio>
#include <vector>
using namespace std;
const int M = 100005;
const int N = 10000005;
#define pb push_back
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,cnt,tot,f[M];vector<int> g[N],vc[M<<2];
int Ind,num[M],siz[M],son[M],top[M],fa[M],dep[M];
int k,scc,dfn[N],low[N],col[N],s[N],in[N];
struct edge{int v,next;}e[M<<1];
void add(int u,int v) {g[u].pb(v);g[v^1].pb(u^1);}
void dfs1(int u,int p)
{
siz[u]=1;fa[u]=p;
dep[u]=dep[p]+1;
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==p) continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int tp)
{
top[u]=tp;num[u]=++Ind;
if(son[u]) dfs2(son[u],tp);
for(int i=f[u];i;i=e[i].next)
if(e[i].v^fa[u] && e[i].v^son[u])
dfs2(e[i].v,e[i].v);
}
void ins(int i,int l,int r,int L,int R,int w)
{
if(L>r || l>R) return ;
if(L<=l && r<=R) {vc[i].push_back(w);return ;}
int mid=(l+r)>>1;
ins(i<<1,l,mid,L,R,w);
ins(i<<1|1,mid+1,r,L,R,w);
}
void add(int u,int v,int w)
{
while(top[u]^top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
ins(1,1,n,num[top[u]],num[u],w);
u=fa[top[u]];
}
if(dep[u]<dep[v]) swap(u,v);
if(u!=v) ins(1,1,n,num[v]+1,num[u],w);
}
void build(int i,int l,int r,int p)
{
int o=vc[i].size(),u=++cnt,v=(cnt+=o);
if(o) add(v-1<<1,v<<1);
else if(p) add(p<<1,v<<1);
for(int j=0;j<o;j++)
{
int w=vc[i][j];add(w,u+j<<1);
if(j) add(u+j-1<<1,w^1),add(u+j-1<<1,u+j<<1);
else if(p) add(p<<1,u<<1),add(p<<1,w^1);
}
if(l==r) return ;
int mid=(l+r)>>1;
build(i<<1,l,mid,v);
build(i<<1|1,mid+1,r,v);
}
void tarjan(int u)
{
low[u]=dfn[u]=++Ind;
s[++k]=u;in[u]=1;
for(int v:g[u])
{
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(in[v])
low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
int v;scc++;
do
{
v=s[k--];
col[v]=scc;in[v]=0;
}while(u!=v);
}
}
signed main()
{
n=cnt=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
e[++tot]=edge{v,f[u]},f[u]=tot;
e[++tot]=edge{u,f[v]},f[v]=tot;
}
dfs1(1,0);dfs2(1,1);m=read();
for(int i=1;i<=m;i++)
{
add(read(),read(),i<<1);
add(read(),read(),i<<1|1);
}
build(1,1,n,0);Ind=0;
for(int i=1;i<=2*cnt;i++)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=m;i++)
if(col[i<<1]==col[i<<1|1])
{puts("NO");return 0;}
puts("YES");
for(int i=1;i<=m;i++)
puts(col[i<<1]<col[i<<1|1]?"1":"2");
}
精准预测（有解结论再探）
题目描述
解法
其实这题我完全是有能力做出来的，一定要把遇到的结论总结好，用的时候才可以行云流水。
考虑每个人的每个时刻具有生存和死亡两种状态，那么我们把这个建成 \(\tt 2sat\)，记 \(A(x,i)\) 表示第 \(x\) 个人的时刻 \(i\) 是生存状态，\(D(x,i)\) 表示第 \(x\) 个人的时刻 \(i\) 是死亡状态，那么我们这样连边：
- 难兄难弟：\(D(x,t)\) 连向 \(D(y,t+1)\)，同时我们把 \(A(y,t+1)\) 连向 \(A(x,t)\)
- 死神来了：\(A(x,t)\) 连向 \(D(y,t)\)，同时我们把 \(A(y,t)\) 连向 \(D(x,t)\)
- 因为生存和死亡的连续性，我们把 \(A(x,t)\) 连向 \(A(x,t-1)\)，把 \(D(x,t)\) 连向 \(D(x,t+1)\)
连出上面的图还是推荐使用对称性，这样就只用连一半了。
然后我们想要优化这张图的点数，发现只有出现过的 \((x,t)\) 和 \((a,T+1)\) 是需要保留的，这样点数一共只有 \(2n+2m\) 个，注意这里不要保留 \((y,t)\)，因为是死亡所以可以等效地连到后面的第一个点（这点常数要卡好）
我们再来分析一下图的性质，由于单看 \(A,B\)，都是时间单调的图，而第二类边有只会带来 \(A\rightarrow B\) 的边，所以说这是一个拓扑图，所以至少存在一组解（全都是死亡状态），并且不存在某个点都是覆盖点 \(x\) 和 \(inv(x)\) 的情况。
现在我们的问题是判断两个生存状态是否能共存，我们可以判断强制选取这两个点之后是否还有解。利用最小字典序的结论：如果当前局面不出现矛盾，那么如果原来有解现在就一定有解。
计算 \(\sum_{1\leq i\leq n,i\not=x} live(x,i)\) 我们可以先把 \(x\)（状态 \(A(x,T+1)\) 简记为 \(x\)）选取了，那么考虑 \(x\) 可以到达的死亡状态的集合是 \(s\)，那么要求 \(i\not\in S\)，此外还要求 \(i\) 不能是初始必死，这样就可以保证当前局面不出现矛盾了。
在 \(\tt dag\) 上要处理出一个点能到达的点集，可以用 \(\tt bitset\)，由于空间限制我们每 \(1000\) 个简单做一次，这样 \(\tt bitset\) 的大小就只用开成 \(1000\) 了，时间复杂度 \(O(\frac{nm}{w})\)
#include <cstdio>
#include <vector>
#include <bitset>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 300005;
const int N = 1005;
#define pb push_back
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
void write(int x)
{
if(x>=10) write(x/10);
putchar(x%10+'0');
}
int k,n,m,ty[M],t[M],x[M],y[M];
int vis[M],s[M],f[M],ans[M],die[M],in[M];
bitset<N> dp[M];vector<int> v[M],g[M];
int id(int i,int j) {return s[i-1]+j+1;}
//x<<1 alive ; x<<1|1 dead
void add(int x,int y) {g[x].pb(y);g[y^1].pb(x^1);}
//something that I mistake x^1 with x .....
void build()
{
for(int i=1;i<=n;i++) v[i].pb(k+1);
for(int i=1;i<=n;i++) s[i]=s[i-1]+v[i].size();
for(int i=1;i<=n;i++)
{
sort(v[i].begin(),v[i].end());
int len=v[i].size();
for(int j=0;j+1<len;j++)
add(id(i,j+1)<<1,id(i,j)<<1);
}
for(int i=1;i<=m;i++)
{
int p1=lower_bound(v[x[i]].begin()
,v[x[i]].end(),t[i])-v[x[i]].begin();
int p2=lower_bound(v[y[i]].begin()
,v[y[i]].end(),t[i]+(!ty[i]))-v[y[i]].begin();
if(!ty[i])
add(id(x[i],p1)<<1|1,id(y[i],p2)<<1|1);
else
add(id(x[i],p1)<<1,id(y[i],p2)<<1|1);
}
for(int i=1;i<=n;i++)
f[i]=id(i,v[i].size()-1)<<1;
}
void dfs(int u)
{
if(vis[u]) return ;vis[u]=1;
if(!in[u]) dp[u].reset();
for(int v:g[u])
dfs(v),dp[u]=dp[u]|dp[v];
}
void work()
{
for(int l=1,r;l<=n;l+=N)
{
r=min(l+N-1,n);
memset(in,0,sizeof in);
memset(vis,0,sizeof vis);
for(int i=l;i<=r;i++)
in[f[i]|1]=1,dp[f[i]|1].set(i-l);
for(int i=1;i<=n;i++) dfs(f[i]);
bitset<N> ban;
for(int i=l;i<=r;i++) if(dp[f[i]][i-l])
die[i]=1,ban[i-l]=1;//then i must die
for(int i=1;i<=n;i++)
ans[i]+=r-l+1-(ban|dp[f[i]]).count();
}
for(int i=1;i<=n;i++)
write(die[i]?0:ans[i]-1),putchar(' ');
}
signed main()
{
k=read();n=read();m=read();
for(int i=1;i<=m;i++)
{
ty[i]=read();t[i]=read();x[i]=read();y[i]=read();
v[x[i]].pb(t[i]);//the crucial points
}
build();work();
}
