[做题笔记] 树形分治/连通块问题练习
切树游戏
题目描述
解法
话说树剖为什么会被卡啊？在洛谷上交了无数发最多 \(90\) 分，在 \(\tt loj\) 上倒是随便过，但是现在已经过了。
首先考虑不带修的暴力 \(dp\)，设 \(dp[u][i]\) 表示以 \(u\) 为最浅点的连通块，异或值为 \(i\) 的方案数。转移就是直接异或卷积，所以我们可以先把每个位置的点 \(\tt FWT\) 正变化，然后就可以直接点值相乘，最后求和再逆变化回去。
如果待修怎么办呢？考虑到我们要求出所有 \(dp[u]\) 的和再逆变换，所以我们再记一个 \(h[u][i]=\sum_{v\in subtree(u)} f[u][i]\)，那么最后维护出 \(h[1]\) 就可以了。这时候可以考虑用动态 \(dp\)，我们再处理出 \(lf[u][i]\) 表示只添加轻儿子时的 \(f[u][i]\)，\(lh[u][i]\) 表示只对轻儿子子树求和所得到的 \(h[u][i]\)
考虑第 \(i\) 位，现在要从节点 \(v\) 的 \((f[v][i],h[v][i],1)\) 变化到重链上父亲 \(u\) 的 \((f[u][i],h[u][i],1)\)，可以右乘上这样一个矩阵：
\[\begin{pmatrix}
lf[u][i]&lf[u][i]&0\\
0&1&0\\
lf[u][i]&lh[u][i]+lf[u][i]&1
\end{pmatrix}
\]
暴力乘可能很慢，考虑到这个矩阵比较稀疏，我们可以把它展开获得常数上的优化：
\[\begin{pmatrix}a_1&b_1&0\\0&1&0\\c_1&d_1&1\end{pmatrix}
\times
\begin{pmatrix}a_2&b_2&0\\0&1&0\\c_2&d_2&1\end{pmatrix}
=
\begin{pmatrix}a_1a_2&b_1+a_1b_2&0\\0&1&0\\a_2c_1+c_2&b_2c_1+d_1+d_2&1\end{pmatrix}
\]
并且我们发现只用维护四个位置上的值，这样就不用记录 \(3\times 3\) 的数组了。
此外因为本题的模数是 \(10007\)，但是在更新重链顶的父亲是，会出现将 \(lf[u][i]\) 做除法的情况，而如果除数是 \(0\) 自然就爆炸了，所以我们把这个数组写成 \(x\times 0^y\) 的形式，除以 \(0\) 的时候将 \(y\) 减 \(1\) 即可。
#include <cstdio>
#include <vector>
using namespace std;
const int M = 30005;
const int N = 130;
const int MOD = 10007;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,q,a[M],inv[M];vector<int> g[M];
struct node
{
int x,y;
node() {x=y=0;}
void init(int a) {a?(x=a,y=0):(x=1,y=1);}
friend node operator * (node A,int b)
{
b%=MOD;
if(!b) A.y++;else A.x=A.x*b%MOD;
return A;
}
friend node operator / (node A,int b)
{
b%=MOD;
if(!b) A.y--;else A.x=A.x*inv[b]%MOD;
return A;
}
int val() {return y?0:x;}
};
void fwt(int *a,int n,int op)
{
for(int i=1;i<n;i<<=1)
for(int j=0,t=i<<1;j<n;j+=t)
for(int k=0;k<i;k++)
{
int fe=a[j+k],fo=a[i+j+k];
a[j+k]=(fe+fo)%MOD;
a[i+j+k]=(fe-fo+MOD)%MOD;
if(op==1) continue;
a[j+k]=a[j+k]*inv[2]%MOD,
a[i+j+k]=a[i+j+k]*inv[2]%MOD;
}
}
int Ind,num[M],id[M],bot[M],t1[M],t2[M];
int siz[M],son[M],fa[M],top[M],e[N][N];
int f[M][N],h[M][N],lh[M][N];node lf[M][N];
void dfs1(int u,int p)
{
fa[u]=p;siz[u]=1;
for(int v:g[u]) if(v^p)
{
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int tp)
{
top[u]=tp;num[u]=++Ind;
bot[u]=num[u];id[Ind]=u;
if(son[u])
dfs2(son[u],tp),bot[u]=bot[son[u]];
for(int v:g[u])
if(v^son[u] && v^fa[u])
dfs2(v,v);
}
void dfs3(int u)
{
for(int i=0;i<m;i++) f[u][i]=e[a[u]][i];
for(int v:g[u]) if(v!=fa[u])
{
dfs3(v);
for(int i=0;i<m;i++)
{
f[u][i]=(f[u][i]+f[u][i]*f[v][i])%MOD;
h[u][i]=(h[u][i]+h[v][i])%MOD;
}
}
for(int i=0;i<m;i++)
h[u][i]=(h[u][i]+f[u][i])%MOD;
}
void dfs4()
{
for(int u=1;u<=n;u++)
{
for(int i=0;i<m;i++)
lf[u][i].init(e[0][i]),lh[u][i]=0;
for(int v:g[u]) if(v^fa[u] && v^son[u])
for(int i=0;i<m;i++)
{
lf[u][i]=lf[u][i]*(f[v][i]+1);
lh[u][i]=(lh[u][i]+h[v][i])%MOD;
}
}
}
struct tree{int a[N],b[N],c[N],d[N];}t[M<<2];
tree operator * (tree A,tree B)
{
tree C;
for(int i=0;i<m;i++)
C.a[i]=C.b[i]=C.c[i]=C.d[i]=0;
for(int i=0;i<m;i++)
{
C.a[i]=A.a[i]*B.a[i]%MOD;
C.b[i]=(A.b[i]+A.a[i]*B.b[i])%MOD;
C.c[i]=(B.a[i]*A.c[i]+B.c[i])%MOD;
C.d[i]=(B.b[i]*A.c[i]+A.d[i]+B.d[i])%MOD;
}
return C;
}
void upd(int i,int x)
{
for(int j=0;j<m;j++)
{
t[i].a[j]=t[i].b[j]=t[i].c[j]=t[i].d[j]
=lf[x][j].val()*e[a[x]][j]%MOD;
t[i].d[j]=(t[i].d[j]+lh[x][j])%MOD;
}
}
void build(int i,int l,int r)
{
if(l==r) {upd(i,id[l]);return ;}
int mid=(l+r)>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
t[i]=t[i<<1|1]*t[i<<1];
}
void fuck(int i,int l,int r,int p)
{
if(l==r) {upd(i,id[l]);return ;}
int mid=(l+r)>>1;
if(mid>=p) fuck(i<<1,l,mid,p);
else fuck(i<<1|1,mid+1,r,p);
t[i]=t[i<<1|1]*t[i<<1];
}
tree ask(int i,int l,int r,int L,int R)
{
if(L<=l && r<=R) return t[i];
int mid=(l+r)>>1;
if(L>mid) return ask(i<<1|1,mid+1,r,L,R);
if(R<=mid) return ask(i<<1,l,mid,L,R);
return ask(i<<1|1,mid+1,r,L,R)
*ask(i<<1,l,mid,L,R);
}
void get(int x)
{
tree zz=ask(1,1,n,num[x],bot[x]);
for(int i=0;i<m;i++)
t1[i]=zz.c[i],t2[i]=zz.d[i];
}
void walk(int x,int c)
{
a[x]=c;
while(x)
{
int y=fa[top[x]];get(top[x]);
if(y) for(int i=0;i<m;i++)
{
lf[y][i]=lf[y][i]/(t1[i]+1);
lh[y][i]=(lh[y][i]-t2[i]+MOD)%MOD;
}
fuck(1,1,n,num[x]);get(top[x]);
if(y) for(int i=0;i<m;i++)
{
lf[y][i]=lf[y][i]*(t1[i]+1);
lh[y][i]=(lh[y][i]+t2[i])%MOD;
}
x=y;
}
}
signed main()
{
n=read();m=read();inv[0]=inv[1]=1;
for(int i=1;i<=n;i++) a[i]=read();
for(int i=2;i<=n;i++)
inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
for(int i=1;i<n;i++)
{
int u=read(),v=read();
g[u].push_back(v);
g[v].push_back(u);
}
for(int i=0;i<m;i++)
e[i][i]=1,fwt(e[i],m,1);
dfs1(1,0);dfs2(1,1);dfs3(1);dfs4();
build(1,1,n);char s[10]={};q=read();
while(q--)
{
scanf("%s",s+1);
if(s[1]=='C')
{
int x=read(),y=read();
walk(x,y);a[x]=y;
}
else
{
get(1);fwt(t2,m,-1);int x=read();
printf("%d\n",t2[x]);
}
}
}
情报中心
题目描述
解法
本题的关键是计算两条路径的并，那么计算并显然就要考察清楚两条路径的位置关系。但是路径的位置关系是不好考虑的，我们可以以点的位置关系代替路径的位置关系。设两条路径分别是 \((u_1,v_1),(u_2,v_2)\)，设 \(t=lca(u_1,u_2)\)，我们考虑在 \(t\) 这个点统计这两条路径的贡献，并且如果我们要求 \(t\) 是交路径上最深的点，情况数很大大减小：
（借用一下 cmd 的图）
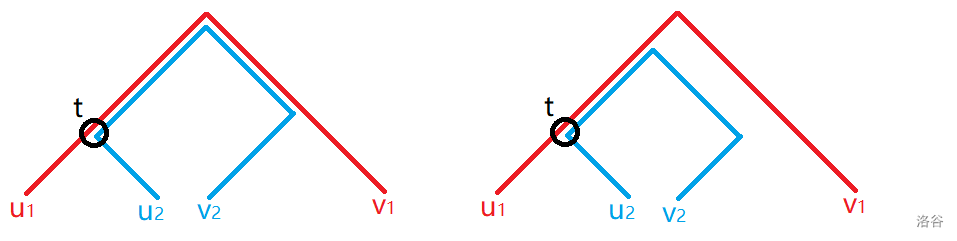
设 \(c(x,y)=dis(x,y)-2\cdot v\)，那么不难发现，这两条路径的贡献是（注意最后要除以 \(2\)）：
\[ans=dis(u_1,u_2)+dis(v_1,v_2)+c(u_1,v_1)+c(u_2,v_2)
\]
因为我们是在 \(u_1,u_2\) 的 \(\tt lca\) 处统计的贡献，所以为了化简这个式子我们可以把 \(dis(u_1,u_2)\) 拆开：
\[w_{v_1}=c(u_1,v_1)+dist(u_1),w_{v_2}=c(u_2,v_2)+dist(u_2)
\]
\[ans=w_{v_1}+w_{v_2}+dis(v_1,v_2)-2\cdot dist(t)
\]
那么我们可以看成是 \(v_1,v_2\) 的带权匹配，由于可以把点权看成新建连在这个点下虚点的边权，所以这个带权匹配就是最大直径，那么就可以用直径合并的方法来维护了，合并两个点集只需要计算 \(6\) 次两两匹配。
那么我们考虑如何确保 \(t\) 是交路径上最深的点，对于路径 \((u,v)\) 设 \(lca=lca(u,v)\)，我们可以在 \([u,lca)\) 这些点的位置放置匹配点 \(v\)；在 \([v,lca)\) 这些位置放置匹配点 \(u\)，那么只有同一个位置上匹配点才能相互匹配。
现在这就是一个线段树合并的形式了，我们可以在 \(u/v\) 插入匹配点，然后在 \(lca\) 在 \(u/v\) 方向的第一个儿子处删除匹配点。以路径的编号建立线段树即可，上传定义为直径合并，时间复杂度 \(O(n\log n)\)
由于我卡常已经卡疯了，下面给出我没有卡过常的代码，只有 \(95\) 分，仅供理解。
#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
const int M = 100005;
#define int long long
const int inf = 1e18;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int T,n,m,k,tot,f[M],fa[M][20];vector<int> b[M];
int lg[M],dep[M],dis[M],dfn[M],dp[M][20];
int ans,cnt,rt[M],ls[M*40],rs[M*40];
struct node{int x,y;}tmp;
struct tree{node a,b;}o,zxy,t[M*40];
//zxy:use to make a clear
struct edge{int v,c,next;}e[M<<1];
//O(nlogn)-O(1) lca
void dfs(int u,int p)//initially dfs
{
dp[++m][0]=u;dfn[u]=m;
fa[u][0]=p;dep[u]=dep[p]+1;
for(int i=1;i<20;i++)
fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v,c=e[i].c;
if(v==p) continue;
dis[v]=dis[u]+c;dfs(v,u);
dp[++m][0]=u;
}
}
int Min(int x,int y)
{
return dep[x]<dep[y]?x:y;
}
void init()//st-table initializion
{
for(int i=2;i<=m;i++) lg[i]=lg[i>>1]+1;
for(int j=1;(1<<j)<=m;j++)
for(int i=1;i+(1<<j)-1<=m;i++)
dp[i][j]=Min(dp[i][j-1],dp[i+(1<<j-1)][j-1]);
}
int lca(int l,int r)//O(1) lca
{
l=dfn[l];r=dfn[r];
if(l>r) swap(l,r);
int k=lg[r-l+1];
return Min(dp[l][k],dp[r-(1<<k)+1][k]);
}
int jump(int x,int y)//the first point of x
{
for(int i=19;i>=0;i--)
if(dep[fa[x][i]]>dep[y])
x=fa[x][i];
return x;
}
int getd(int u,int v)
{
return dis[u]+dis[v]-2*dis[lca(u,v)];
}
//segment-tree merge
int upd(int &mx,node u,node v)
{
if(!u.x || !v.x) return 0;
int c=u.y+v.y+getd(u.x,v.x);
if(c>mx) {mx=c;return 1;}
return 0;
}
int comb(tree &s,tree u,tree v)
{
int ret=0,mx=-inf;
//must consider the cases below
if(!u.a.x && !u.a.y) {s=v;return -inf;}
if(!v.a.x && !v.a.y) {s=u;return -inf;}
if(upd(mx,u.a,v.a)) s=tree{u.a,v.a};
if(upd(mx,u.a,v.b)) s=tree{u.a,v.b};
if(upd(mx,u.b,v.a)) s=tree{u.b,v.a};
if(upd(mx,u.b,v.b)) s=tree{u.b,v.b};
ret=mx;
if(upd(mx,u.a,u.b)) s=tree{u.a,u.b};
if(upd(mx,v.a,v.b)) s=tree{v.a,v.b};
return ret;
}
void up(int x)
{
if(!ls[x]) {t[x]=t[rs[x]];return ;}
if(!rs[x]) {t[x]=t[ls[x]];return ;}
comb(t[x],t[ls[x]],t[rs[x]]);
}
void ins(int &x,int l,int r,int id)
{
if(!x) x=++cnt;
if(l==r) {t[x].a=tmp;return ;}
int mid=(l+r)>>1;
if(mid>=id) ins(ls[x],l,mid,id);
else ins(rs[x],mid+1,r,id);
up(x);
}
void del(int &x,int l,int r,int id)
{
if(l==r) {t[x]=zxy;return ;}
int mid=(l+r)>>1;
if(mid>=id) del(ls[x],l,mid,id);
else del(rs[x],mid+1,r,id);
up(x);
}
int merge(int x,int y)
{
if(!x || !y) return x|y;
comb(t[x],t[x],t[y]);
ls[x]=merge(ls[x],ls[y]);
rs[x]=merge(rs[x],rs[y]);
return x;
}
void dfs2(int u)
{
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa[u][0]) continue;
dfs2(v);
ans=max(ans,comb(o,t[rt[u]],t[rt[v]])-2*dis[u]);
rt[u]=merge(rt[u],rt[v]);
}
for(int v:b[u]) del(rt[u],1,k,v);
}
void work()
{
n=read();ans=-inf;
for(int i=1;i<n;i++)
{
int u=read(),v=read(),c=read();
e[++tot]=edge{v,c,f[u]},f[u]=tot;
e[++tot]=edge{u,c,f[v]},f[v]=tot;
}
dfs(1,0);init();
//handle the queries
node emp;k=read();
for(int i=1;i<=k;i++)
{
int u=read(),v=read(),c=read(),d=getd(u,v);
int x=lca(u,v),p=jump(u,x),q=jump(v,x);
if(u!=x)
{
tmp=node{v,d-2*c+dis[u]};
ans=max(ans,comb(o,tree{tmp,emp},t[rt[u]])-2*dis[u]);
ins(rt[u],1,k,i);b[p].push_back(i);
}
if(v!=x)
{
tmp=node{u,d-2*c+dis[v]};
ans=max(ans,comb(o,tree{tmp,emp},t[rt[v]])-2*dis[v]);
ins(rt[v],1,k,i);b[q].push_back(i);
}
}
dfs2(1);
if(ans<=-inf) puts("F");
else printf("%lld\n",ans/2);
//clear all // attention!
for(int i=1;i<=n;i++)
f[i]=rt[i]=dis[i]=dfn[i]=0,b[i].clear();
for(int i=1;i<=cnt;i++)
ls[i]=rs[i]=0,t[i]=zxy;
tot=cnt=n=m=k=0;
}
signed main()
{
T=read();
while(T--) work();
}
完美的集合
题目描述
解法
这题竟然只写了两节课，已经是奇迹了，话说这种题如果不口胡写代码是真的爽。
首先可以考虑求出完美集合的价值，这个可以用树上依赖背包，也就是把 \(\tt dfn\) 序离线下来，然后每次可以考虑一个点 \(u\) 是可以选择它或者跳过它的子树，那么就是普通背包问题了。
那么我们对某个点 \(x\) 能测试的所有点做树上依赖背包，可以求出以点为测试中心 \(x\) 的完美连通块个数。考虑连通块计数的经典容斥 点数-边数=1，并且对一种方案所有可作为测试中心的点一定构成连通块，那么我们再求出点 \(x,y\) 都是为测试中心的完美联通块个数即可，这两者的方案数都是形如 \({cnt\choose k}\bmod 5^{23}\) 的形式。
那么现在的问题就变成了如何求 \({cnt\choose k}\bmod 5^{23}\)，虽然我不会扩展卢卡斯，但是我们可以仿照 \(\tt ex\_lucas\) 的方法，首先我们把 \(n!\) 的所有 \(5\) 的质因子分离出来，然后考虑计算下面这个函数：
\[f(n)=\prod_{i=1}^n [i\perp 5]i
\]
那么剩下的数和求乘就是 \(\prod_{i} f(\frac{n}{5^i})\)，考虑到 \(5^{23}=0\bmod 5^{23}\)，所以我们可以把它写成生成函数的形式：
\[f_n(x)=\prod_{i=1}^n[i\perp 5](x+i)
\]
那么如果 \(n\) 是 \(5\) 的倍数，我们只用保留 \(f_n(x)\) 的 \(23\) 项即可。那么可以考虑多项式倍增，假设现在要求出 \(f_{10n}(x)\)，可以先递归解决 \(f_{5n}(x)\)，然后利用二项式定理求出 \(f_{5n}(x+5n)\)，把它们卷起来即可，由于 \(n\) 不一定是 \(10\) 的倍数所以可能最后需要把一些零散的项卷上去。
计算组合数的复杂度应该可以忽略不记（\(23^2\times \log_5n\times n\)），所以总时间复杂度 \(O(n^2m)\)
#include <cstdio>
#include <iostream>
#include <array>
using namespace std;
#define int long long
#define ll __int128
const int M = 105;
const int p = 11920928955078125;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,t,mx,ans,tot,f[M],a[M],w[M],ok[M];
int cnt,id[M],dfn[M],out[M],C[30][30];
struct node{int x,y;}dp[M][10005];
struct edge{int v,c,next;}e[M<<1];
void pre(int u,int fa,int d,int &s)
{
if((ll)a[u]*d<=t) s|=(1ll<<u);
for(int i=f[u];i;i=e[i].next)
if(e[i].v^fa) pre(e[i].v,u,d+e[i].c,s);
}
void dfs(int u,int fa)
{
dfn[u]=++cnt;id[cnt]=u;
for(int i=f[u];i;i=e[i].next)
if(e[i].v^fa) dfs(e[i].v,u);
out[dfn[u]]=cnt;
}
void trans(node &a,node b,int c)
{
if(!b.y) return ;//important judge
if(a.x<b.x+c) a.x=b.x+c,a.y=0;
if(a.x==b.x+c) a.y+=b.y;
}
void work(int s,int u,int v)
{
cnt=0;dfs(u,0);
for(int i=0;i<=n;i++)
for(int j=0;j<=m;j++)
dp[i][j].x=dp[i][j].y=0;
for(int i=0;i<=m;i++) dp[0][i].y=1;
for(int i=1;i<=n;i++)
{
int u=id[i];//choose i
if(s>>u&1) for(int j=m;j>=w[u];j--)
trans(dp[i][j],dp[i-1][j-w[u]],a[u]);
if(i>1 && (dfn[v]<i || dfn[v]>out[i]))
for(int j=0;j<=m;j++)
trans(dp[out[i]][j],dp[i-1][j],0);
}
}
int count(int n)
{
int res=0;while(n) res+=n/=5;
return res;
}
array<ll,25> zxy(int n)
{
ll a[25]={},b[25]={};b[0]=1;array<ll,25> res;
if(n==0) {res.fill(0);res[0]=1;return res;}
int tn=n/10*5;res=zxy(tn);
for(int i=1;i<23;i++) b[i]=b[i-1]*tn%p;
//binomial theorem
for(int i=0;i<23;i++)
for(int j=i;j<23;j++)
a[i]=(a[i]+res[j]*C[j][j-i]%p*b[j-i])%p;
//convolution
for(int i=22;i>=0;i--)
{
ll t=0;
for(int j=0;j<=i;j++)
t=(t+res[j]*a[i-j])%p;
res[i]=t;
}
//some remaining numbers
for(;n>2*tn;n--) if(n%5)
for(int i=22;i>=0;i--)
res[i]=(res[i]*n+(i?res[i-1]:0))%p;
return res;
}
ll fac(int n)
{
ll res=1;
while(n) res=res*zxy(n)[0]%p,n/=5;
return res;
}
void exgcd(int a,int b,int &x,int &y)
{
if(!b) {x=1;y=0;return ;}
exgcd(b,a%b,y,x);y-=(a/b)*x;
}
int comb(int n)
{
if(n<k) return 0;
int d=count(n)-count(k)-count(n-k);
int t=fac(n-k)*fac(k)%p,x=0,y=0;
exgcd(t,p,x,y);x=(x%p+p)%p;
x=x*fac(n)%p;
while(d--) x=x*5%p;
return x;
}
void calc(int u,int fa)
{
work(ok[u],u,0);
if(dp[n][m].x==mx)
ans=(ans+comb(dp[n][m].y))%p;
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa) continue;
calc(v,u);
work(ok[u]&ok[v],u,v);
if(dp[n][m].x==mx)
ans=(ans-comb(dp[n][m].y))%p;
}
}
signed main()
{
n=read();m=read();k=read();t=read();
for(int i=1;i<=n;i++) w[i]=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read(),c=read();
e[++tot]=edge{v,c,f[u]},f[u]=tot;
e[++tot]=edge{u,c,f[v]},f[v]=tot;
}
for(int i=1;i<=n;i++) pre(i,0,0,ok[i]);
for(int i=1;i<=n;i++)
work((1ll<<n+1)-1,i,0),mx=max(mx,dp[n][m].x);
for(int i=0;i<=22;i++)
{
C[i][0]=1;
for(int j=1;j<=i;j++)
C[i][j]=(C[i-1][j-1]+C[i-1][j])%p;
}
calc(1,0);
printf("%lld\n",(ans%p+p)%p);
}
