#4 CF568E & CF613E & CF587D
Longest Increasing Subsequence
题目描述
解法
首先有一个关键的 \(\tt observation\):由于本题求的是最长上升子序列,所以在求解最优解是每个数只出现一次这个限制是可以忽略的,因为最长上升子序列不可能包含重复的数。
考虑魔改一下传统的 \(\tt LIS\) 做法:设 \(f_i\) 表示长度为 \(i\) 的最长上升子序列的结尾最小值,\(g_i\) 表示这个结尾的位置。那么非空位可以直接转移,空位可以双指针转移,暴力枚举所有填入的数即可。
再考虑如何构造出最后的答案,对于非空位我们可以记录 \(l_i\) 表示以 \(i\) 结尾的最长上升子序列长度,\(p_i\) 表示这个最优序列的上一个位置。所以对于非空位我们可以直接跳到上一个位置,对于空位可以直接枚举上一个位置,复杂度没问题,总时间复杂度 \(O((n+m)k)\)
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
const int M = 100005;
const int inf = 0x3f3f3f3f;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,t,a[M],b[M],c[M],lst[M];
int f[M],g[M],l[M],p[M];map<int,int> mp;
int get(int x)
{
return b[lower_bound(b+1,b+1+m,x)-b-1];
}
signed main()
{
n=read();
for(int i=1,z=0;i<=n;i++)
{
a[i]=read();f[i]=inf;
lst[i]=z;if(a[i]==-1) z=i;
}
m=read();
for(int i=1;i<=m;i++) mp[b[i]=read()]++;
sort(b+1,b+1+m);
for(int i=1;i<=n;i++)
{
if(a[i]!=-1)
{
int j=lower_bound(f+1,f+1+t,a[i])-f;
p[i]=g[j-1];l[i]=j;
g[j]=i;f[j]=a[i];
if(f[t+1]<inf) t++;
continue;
}
int j=t+1;
for(int k=m;k>=1;k--)
{
while(j>0 && f[j-1]>=b[k]) j--;
f[j]=b[k];g[j]=i;
}
if(f[t+1]<inf) t++;
}
int nl=t,nv=f[t],i=g[t],j=1;
while(nl--)
{
if(a[i]!=-1)
{
if(a[p[i]]==-1) nv=get(a[i]);
i=p[i];continue;
}
c[i]=nv;mp[nv]--;int j=0;
for(int k=i-1;k>=1;k--)
if(l[k]==nl && a[k]<nv && a[k]!=-1)
{j=k;break;}
if(j) i=j;
else i=lst[i],nv=get(nv);
}
for(int i=1,j=1;i<=n;i++)
{
if(a[i]!=-1) c[i]=a[i];
else if(!c[i])
{
while(!mp[b[j]]) j++;
c[i]=b[j];mp[b[j]]--;
}
}
for(int i=1;i<=n;i++)
printf("%d ",c[i]);
puts("");
}
Puzzle Lover
题目描述
解法
一定要注意是 \(2\times n\) 的矩阵,不是 \(n\times m\) 的矩阵哦,这启示我们可以去使用讨论法。
我们先 \(m=1/2\) 的情况特判掉,然后考虑答案的形式一定是这样(嫖个 大佬 的图):
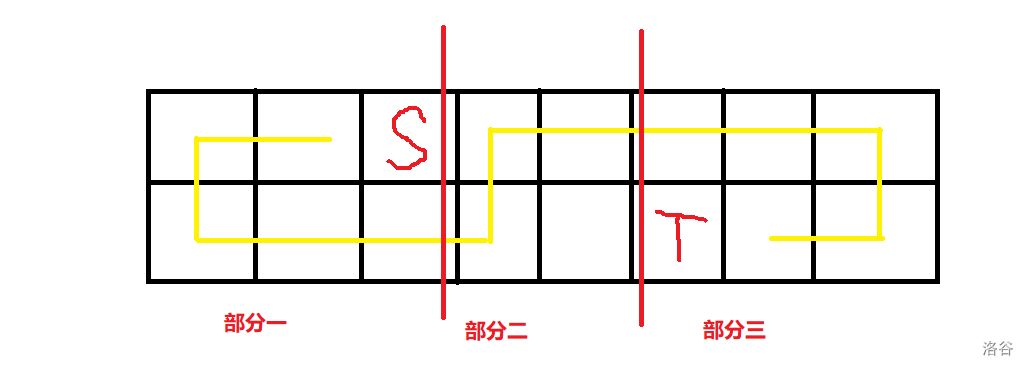
那么所有路径都可以分成这三个部分,我用自然语言描述一下:
- 部分一:从起点往左走,然后走到某个点绕回来,构成上下两个等长的段。
- 部分二:如果新到这一列,那么可以走到同列的另一行,否则只能走到下一列。
- 部分三:从部分二出来之后走到某个点绕回来,构成上下两个等长的段。
发现部分一和部分三都是可以通过哈希轻易解决的,部分二需要决策貌似有点难搞。
那么我们考虑只有部分二怎么处理,设 \(f[i][j][k]\) 表示现在在 \((i,j)\),匹配到目标串的第 \(k\) 位的方案数,并且一下步只能走下一列;设 \(g[i][j][k]\) 表示现在在 \((i,j)\),匹配到了字符串的第 \(k\) 位的方案数,下一步可以换行或者走下一列,那么这两个数组交替转移即可(实际上就是把能不能换列记录下来了):
然后再把部分一和部分三考虑进去,发现现在就可以整体 \(dp\) 了,我们枚举部分一的两个等长段,匹配上目标串的一个前缀,作为部分二 \(dp\) 的初始化;\(dp\) 之后再枚举部分三的两个等长段,匹配上目标串的一个后缀,来用 \(dp\) 值统计答案。
统计答案还有一些细节:做完一次之后可以把目标串翻转然后再做一次,对于不需要部分二的方案我们算了两次,需要除掉。时间复杂度 \(O(n^2)\)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 2005;
const int MOD = 1e9+7;
#define ull unsigned long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,ans,gs,g[2][M][M],f[2][M][M];
char s[2][M],t[M];ull h1[2][M],h2[2][M],h[M],pw[M];
void add(int &x,int y) {x=(x+y)%MOD;}
ull get1(int l,int r,int id) {return h1[id][r]-h1[id][l-1]*pw[r-l+1];}
ull get2(int l,int r,int id) {return h2[id][l]-h2[id][r+1]*pw[r-l+1];}
void dp()
{
memset(f,0,sizeof f);
memset(g,0,sizeof g);
for(int i=1;i<=m;i++)
h[i]=h[i-1]*371+t[i];
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
for(int k=j;k>=1;k--)
{
int len=2*(j-k+1);
if(len>m) break;
ull ha=get1(k,j,i),hb=get2(k,j,i^1);
if(ha+pw[j-k+1]*hb==h[len])
{
if(len==m) gs++;
else g[i][j][len]=1;
}
}
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
if(s[i][j]==t[1]) g[i][j][1]=1;
for(int i=m;i>=1;i--)
h[i]=h[i+1]*371+t[i];//reverse the hash
for(int k=1;k<m;k++)
for(int j=1;j<=n;j++)
for(int i=0;i<2;i++)
{
if(j<n && s[i][j+1]==t[k+1])
add(f[i][j+1][k+1],g[i][j][k]),
add(f[i][j+1][k+1],f[i][j][k]);
if(s[i^1][j]==t[k+1])
add(g[i^1][j][k+1],f[i][j][k]);
}
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
{
if(s[i][j]==t[m])
{
add(ans,f[i][j-1][m-1]);
add(ans,g[i][j-1][m-1]);
}
for(int k=j;k<=n;k++)
{
int len=(k-j+1)*2;
if(len>m) break;
ull ha=get1(j,k,i^1),hb=get2(j,k,i);
if(ha*pw[k-j+1]+hb==h[m-len+1])
{
if(len==m) gs++;
else add(ans,f[i][j-1][m-len]),
add(ans,g[i][j-1][m-len]);
}
}
}
}
signed main()
{
scanf("%s%s%s",s[0]+1,s[1]+1,t+1);
n=strlen(s[0]+1);m=strlen(t+1);pw[0]=1;
if(m==1)
{
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
ans+=s[i][j]==t[1];
printf("%d\n",ans);
return 0;
}
if(m==2)
{
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++) if(s[i][j]==t[1])
ans+=(s[i^1][j]==t[2])+(s[i][j-1]==t[2])
+(s[i][j+1]==t[2]);
printf("%d\n",ans);
return 0;
}
for(int i=1;i<M;i++) pw[i]=pw[i-1]*371;
for(int i=0;i<2;i++)
{
for(int j=1;j<=n;j++)
h1[i][j]=h1[i][j-1]*371+s[i][j];
for(int j=n;j>=1;j--)
h2[i][j]=h2[i][j+1]*371+s[i][j];
}
dp();reverse(t+1,t+m+1);dp();
add(ans,gs/2);printf("%d\n",ans);
}
Duff in Mafia
题目描述
解法
我真心觉得本题的一些性质可以大讨论,但是太难写了所以我放弃了,还是走算法的正途吧。
思考匹配带来的限制,一言以蔽之:匹配的两个边之间不能有共同端点,那么我们考虑两边带来的限制。这可以转化成一个 \(\tt 2-sat\) 问题,我们用下面的方法建图:
- 设 \(x_i\) 表示边 \(i\) 最终删除,\(x_i'\) 表示边 \(i\) 最终不删除,二分答案 \(c\)
- 如果边权 \(>c\),代表这条边不能删除,\(x_i\) 连向 \(x_i'\)
- 对于两个共点的边 \(i,j\),不能同时被删除,\(x_i\) 连向 \(x_j'\)
- 对于两个共点同色的边 \(i,j\),在最后不能共存,\(x_i'\) 连向 \(x_j\)
考虑共点同色的边数 \(\leq 2\),所以第三类边可以直接暴力连。但是第二类边需要优化建图,一个很显然的思考是用前后缀拼出这个 \(i\not=j\),那么我们就建两层点分别表示前后缀的虚点,稍微想一下怎么连边即可。
为了卡常我们可以只在二分的时候建第一类边,时间复杂度 \(O(n\log n)\)
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#include <stack>
using namespace std;
#define pb push_back
const int M = 1000005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
//choose : x , not choose : x+m
int n,m,k,cnt,a[M],b[M],c[M],d[M],id[M];
int num,Ind,low[M],dfn[M],col[M],in[M];
vector<int> g[M],v[M];stack<int> s;
void add(int x,int y) {g[x].pb(y);};
void tarjan(int u)
{
low[u]=dfn[u]=++Ind;
s.push(u);in[u]=1;
for(auto v:g[u])
{
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(in[v])
low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
int v=0;num++;
do {
v=s.top();s.pop();
col[v]=num;in[v]=0;
}while(v!=u);
}
}
int check(int x)
{
for(int i=1;i<=m;i++)
if(d[i]>x) add(i,i+m);
for(int i=1;i<=cnt;i++) dfn[i]=0;
num=Ind=0;
for(int i=1;i<=cnt;i++)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=m;i++)
if(d[i]>x) g[i].pop_back();
for(int i=1;i<=m;i++)
if(col[i]==col[i+m]) return 0;
return 1;
}
signed main()
{
n=read();m=read();cnt=m<<1;
for(int i=1;i<=m;i++)
{
a[i]=read();b[i]=read();
c[i]=read();d[i]=read();
v[a[i]].pb(i);v[b[i]].pb(i);
}
for(int i=1;i<=n;i++)
{
sort(v[i].begin(),v[i].end(),
[](int &x,int &y){return c[x]<c[y];});
for(int j=0,k=0,l=v[i].size();j<l;j=k)
{
while(k<l && c[v[i][j]]==c[v[i][k]]) k++;
if(k-j>2) {puts("No");return 0;}
if(k-j==2)
add(v[i][j]+m,v[i][j+1]),
add(v[i][j+1]+m,v[i][j]);
}
int lst=0;
for(auto x:v[i])
{
int y=++cnt;
if(lst) add(y,lst),add(x,lst);
add(y,x+m);lst=y;
}
reverse(v[i].begin(),v[i].end());lst=0;
for(auto x:v[i])
{
int y=++cnt;
if(lst) add(y,lst),add(x,lst);
add(y,x+m);lst=y;
}
}
int l=0,r=1e9,ans=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
if(ans==-1) {puts("No");return 0;}
check(ans);
for(int i=1;i<=m;i++)
if(col[i]<col[i+m]) id[++k]=i;
puts("Yes");printf("%d %d\n",ans,k);
for(int i=1;i<=k;i++) printf("%d ",id[i]);
}



