Atcoder Grand Contest 006
Rotate 3x3
题目描述
解法
首先观察到一个性质:操作存在可逆性,换句话说就是如果存在解,那么从任意可达的状态出发都可以得到解。
\(\tt Oneindark\):根据这个性质我们可以尝试调整使得只有极小部分不合法,最后再解决它们。
为了简化问题我们把每一列看成代表数字(也就是中间列的数字)和颜色(上下是顺序还是反序:白\(/\)黑),这转化成了一个长度为 \(n\) 的排列问题。
那么我们先从前往后调整,首先让当前位置的数字对上,然后可以通过下面的方法调整当前位置的颜色:a b c d->[c] [b] [a] d->[c] [d] a b->[a] d c b
所以最后只会剩下三个数颜色和数字待考虑,可以考察有解的必要条件:奇数位置和偶数位置的黑点个数都是偶数。由于以偶数位置为中心的交换只会改变偶数位置黑点个数的奇偶性,我们可以把初始的奇偶性记录下来,再异或上交换次数,就得到了最后偶数位置黑点的奇偶性(奇数位置也同理)
然后我们再尝试在这个必要条件的基础上构造,发现按照下列方法一定能构造出来:
3 4 [5] 6 [7] -> 5 [4] [3] 6 [7] -> 5 [4] 7 [6] 3
-> 5 6 [7] 4 3 -> 5 6 [3] [4] 7 -> 3 [6] [5] [4] 7 -> 3 4 5 6 7
所以一开始做完一些琐碎的判断之后,有解的充要条件就是 初始偶数位置黑点数^奇数位置逆序对=1 & 初始奇数位置黑点数^偶数位置逆序对=1
#include <cstdio>
#include <cstring>
const int M = 100005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,a[4][M],b[M],cnt[2],inv[2];
int Abs(int x)
{
return x>0?x:-x;
}
int lowbit(int x)
{
return x&(-x);
}
void add(int x)
{
for(int i=x;i<=n;i+=lowbit(i))
b[i]^=1;
}
int ask(int x)
{
int r=0;
for(int i=x;i>0;i-=lowbit(i))
r^=b[i];
return r;
}
signed main()
{
n=read();
for(int i=1;i<=3;i++)
for(int j=1;j<=n;j++)
a[i][j]=read();
for(int i=1;i<=n;i++)
{
if(Abs(a[2][i]-a[1][i])!=1
|| Abs(a[2][i]-a[3][i])!=1
|| a[2][i]%3!=2
|| ((a[2][i]+1)/3)%2!=i%2)
{puts("No");return 0;}
if(a[1][i]>a[3][i]) cnt[i&1]++;
}
for(int w=0;w<2;w++)
{
memset(b,0,sizeof b);
for(int i=n;i>=1;i--) if(i%2==w)
{
int w=(a[2][i]+1)/3;
inv[i&1]+=ask(w);add(w);
}
}
if((inv[0]^cnt[1])%2 || (inv[1]^cnt[0])%2)
puts("No");
else puts("Yes");
}
Blackout
题目描述
给定 \(n\) 个点 \(m\) 条边构成的有向图,如果 \((x,y),(y,z)\) 都有边,那么我们可以连边 \((z,x)\),请问最后的图最多有多少条边。
\(n,m\leq 10^5\)
解法
打出暴搜之后发现答案很容易就变成完全图,并且我们发现 \(len\bmod 3=0\) 的环不是完全图,但是 \(len\bmod 3\not=0\) 的环是完全图。我们可以给出合理的猜测:如果对原图三染色失败,那么最后可以得到完全图,有向图三染色的含义是:如果 \((u,v)\) 有边,那么 col[v]=(col[u]+1)%3
首先我们考察另一个东西,如果对原图三染色成功,那么可以把原图分成三层,只有 i,(i+1)%3 这两层之间才连边。考虑证明引理:i,(i+1)%3 层间的边是连满的(我们称之为完全分层图)。
证明考虑归纳法,每次向完全分层图添加一个点,就像下图,我们先添加绿色的边,再添加蓝色的边得到新的完全分层图:
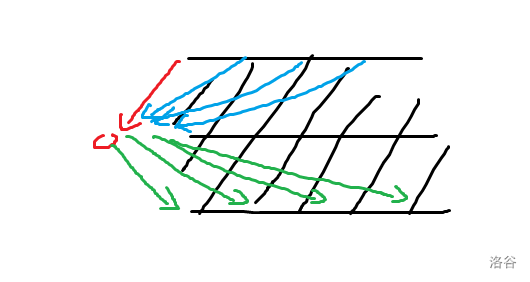
那么如果有一个点的加入使得图不能分层,一定会产生重边(也就是 (u,v),(v,u)),进而产生自环,所以一定会产生完全图(这里把 \(3\) 个点的所有情况讨论一下就可以证明了)
那么直接用结论做就可以了,时间复杂度 \(O(n)\)
#include <cstdio>
const int M = 100005;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,fl,cn,ce,tot,ans,f[M],c[3],vis[M],col[M];
struct edge{int v,c,next;}e[M<<1];
void dfs(int u)
{
c[col[u]]++;vis[u]=1;cn++;
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v,w=(col[u]+e[i].c+3)%3;
ce+=(e[i].c==1);
if(!vis[v]) col[v]=w,dfs(v);
else if(col[v]!=w) fl=1;
}
}
signed main()
{
n=read();m=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
e[++tot]=edge{v,1,f[u]},f[u]=tot;
e[++tot]=edge{u,-1,f[v]},f[v]=tot;
}
for(int i=1;i<=n;i++)
{
if(vis[i]) continue;
c[0]=c[1]=c[2]=fl=cn=ce=0;
dfs(i);
if(fl) ans+=cn*cn;
else if(c[0] && c[1] && c[2])
ans+=c[0]*c[1]+c[1]*c[2]+c[2]*c[0];
else ans+=ce;
}
printf("%lld\n",ans);
}




