#2 CF521E & CF527E & CF516E
CF521E Cycling City
题目描述
给定一张 \(n\) 个点 \(m\) 条边的无向简单图,问图中能否找到两个点,使得两个点之间至少有三条除端点之外点不交的路径。
\(n,m\leq 2\cdot 10^5\)
解法
我根本做不出这题,首先有一个奇妙的题目转化:两个点之间有三条点不交路径的充要条件是两点间有两个相交的环,它们显然可以互相推导。
转化成环问题之后不知道好做了多少!我们可以求原问题的 \(\tt dfs\) 树,那么问题就变成了找被非树边覆盖至少两次的树边,非树边可以暴力往上跳,因为每个点最多被跳两次所以时间复杂度 \(O(n)\)
现在的问题变成了给出一个合法的构造,假设这两条非树边是 \((a,b),(c,d)\),\(d\) 点比 \(b\) 点更深,这三条路径分别是:d->lca、d->b->a->lca、d->c->lca,从下图可以很好地看出来:
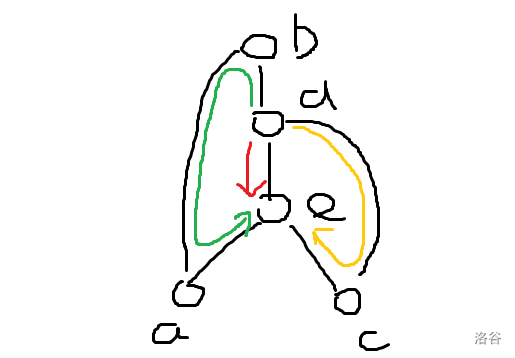
还有一些 \(\tt corner\ case\)(比如 \(a,c\) 祖先儿子关系、重合)就留给读者自己讨论了。
总结
分析答案的结构,把不同的图论意义之间做等价转化。
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 200005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,tot,f[M],vis[M],dep[M],fa[M];
int k,tmp[M],cx[M],cy[M];
struct edge{int v,next;}e[M<<1];
int lca(int u,int v)
{
while(u!=v)
{
if(dep[u]>dep[v]) u=fa[u];
else v=fa[v];
}
return u;
}
void fuck(int x,int y)
{
for(int i=x;i!=y;i=fa[i])
tmp[++k]=i;
tmp[++k]=y;
}
void print()
{
printf("%d ",k);
for(int i=1;i<=k;i++)
printf("%d ",tmp[i]);
k=0;puts("");
}
void get(int a,int b,int c,int d)
{
if(dep[b]>dep[d])
swap(a,c),swap(b,d);
int e=lca(a,c);
puts("YES");
//d->lca
fuck(e,d);
reverse(tmp+1,tmp+k+1);print();
//d->b->a->lca
fuck(d,b);fuck(a,e);print();
//d->c->lca
tmp[++k]=d;fuck(c,e);print();
exit(0);
}
void dfs(int u)
{
vis[u]=1;dep[u]=dep[fa[u]]+1;
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(!vis[v])
{
fa[v]=u;dfs(v);
continue;
}
if(v==fa[u] || dep[v]>dep[u]) continue;
for(int x=u;x!=v;x=fa[x])
{
if(cx[x])
get(cx[x],cy[x],u,v);
else
cx[x]=u,cy[x]=v;
}
}
}
signed main()
{
n=read();m=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
e[++tot]=edge{v,f[u]},f[u]=tot;
e[++tot]=edge{u,f[v]},f[v]=tot;
}
for(int i=1;i<=n;i++)
if(!vis[i]) dfs(i);
puts("NO");
}
CF527E Data Center Drama
题目描述
给定一个 \(n\) 个点 \(m\) 条边的联通无向图,你需要加入尽可能少的边,然后给所有边定向,使得每个点的出入度都是偶数,边既可以是自环也可以是重边。
\(n\leq 10^5,m\leq 2\cdot 10^5\)
解法
感觉就是一道构造题,我们先找必要条件:在无向图的意义下,每个点的度数都要是偶数(因为每一条边要不然贡献入度要不然贡献出度),边的总数是偶数。
我们根据必要条件来构造,那么显然需要把每个点的度数补成偶数。我们先任意把两个奇数点配对然后连边,如果最后总边数为奇数那么我们补一个自环。
考虑现在得到的图每个点都是偶数,这个图一定是存在欧拉回路的。我们考虑用欧拉回路求出一个包含所有边的大环,然后给环上的边依次正反定向:a->b<-c->d<-e->f<-a,那么显然最后每个点的入度和出度都是偶数。
小细节:本题由于存在自环不能用直接选择一条边 \(\tt dfs\) 的方法,而应用循环 \(\tt dfs\),在回溯的时候把当前边加入欧拉回路中(这应该是目前最不易出错的欧拉回路写法)
总结
现在我遇到的欧拉回路模型:给边定向使得入度等于出度;求出一个包含所有边的大环。边定向问题可以考虑欧拉回路。
#include <cstdio>
const int M = 100005;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,cnt,tot,f[M],cur[M],a[M],d[M];
int vis[M<<3];
struct edge{int v,id,next;}e[M<<3];
void add(int u,int v)
{
d[u]++;d[v]++;cnt++;
e[++tot]=edge{v,cnt,f[u]},f[u]=tot;
e[++tot]=edge{u,cnt,f[v]},f[v]=tot;
}
void dfs(int u)
{
for(int &i=f[u];i;i=e[i].next)
{
if(vis[e[i].id]) continue;
vis[e[i].id]=1;
int v=e[i].v;dfs(v);cnt++;
if(cnt&1) printf("%d %d\n",u,v);
else printf("%d %d\n",v,u);
}
}
signed main()
{
n=read();m=read();
for(int i=1;i<=m;i++)
add(read(),read());
for(int i=1;i<=n;i++)
if(d[i]&1) a[++k]=i;
for(int i=1;i<=k;i+=2)
add(a[i],a[i+1]);
if(cnt&1) add(1,1);
for(int i=1;i<=n;i++) cur[i]=f[i];
printf("%d\n",cnt);
cnt=0;dfs(1);
}
CF516E Drazil and His Happy Friends
题目描述
还说如果这题魔改一下题面就会很有意思,以后再说。
解法
首先考虑如何判断有解,根据我微薄的数论知识,令 \(d=\gcd(n,m)\),我们考虑把模 \(d\) 同余的男生和女生都放在一组,那么只有组内的快乐才会传递,那么有解的充要条件是每组都至少有一个人快乐。
如果有解那么 \(d\leq 2\cdot 10^5\),我们可以尝试把每一组单独讨论了。每一组的结束时间可以转化成每个人快乐时间的最大值,发现还是难以处理。使用拆分法,原问题是男女生混合快乐的过程(?),那么为了简化问题我们把男女生拆开,然后把快乐的传递都放在女生处(我只是觉得女孩子之间就是好啊),这样男女生就可以分别计算了。
具体来说,我们考虑某个男生 \(j\bmod n\) 在时刻 \(j\) 因为女生 \(j\bmod m\) 变快乐了,那么在 \(n\) 个单位时间后他可以让女生 \((j+n)\bmod m\) 变快乐,这可以理解成女生快乐的直接传递,我们把这个关系建成图:
- 女生 \(j\) 向女生 \((j+n)\bmod m\) 连一条长度为 \(n\) 的边,表示快乐的传递。
- 如果女生 \(i\) 初始就是快乐的,那么由源点向 \(i\) 连一条长度为 \(i\) 的边,表示从时刻 \(i\) 开始传递快乐。
- 如果男生 \(i\) 初始就是快乐的,那么由源点向 \(i\bmod m\) 连一条长度为 \(i\) 的边。
我们从源点开始跑最短路就可以求出每个人的快乐时间,然后把初始不快乐女生的最短路取最大值就得到了答案。
但是直接跑最短路显然会超时,我们考虑第二、三类边的数量是有限的,可以由第一类边来重构这个环。新环上相邻两个点原来的距离是 \(n\),在新环上我们只保留二、三类边所连接的点,然后对于环上每一段我们计算最后一个点的到达时间,取最大值即可,时间复杂度 \(O(d\log d)\)
怎么对环进行重标号呢?设点 \(x\) 是由 \(0\) 走 \(i\) 步达到的,那么 \(in=x\bmod m\),所以 \(i=x\cdot n^{-1}\bmod m\),我们用 \(\tt exgcd\) 求出逆元就可以重构环了。
总结
拆分法的使用十分精妙,本题是把两个东西之间的影响拆开,都放在一个东西上,可见把限制集中常常是好事。
对于巨大范围的东西常常需要观察结构,比如本题的第一类边是环的结构,就可以从这个结构出发解题了。
//Why you always in a mood?
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 200005;
#define pb push_back
#define int long long
#define Morisummer {puts("-1");return 0;}
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,ans,s[M],a[M],p[M];
vector<int> A[M],B[M];
int exgcd(int a,int b,int &x,int &y)
{
if(!b) {x=1;y=0;return a;}
int d=exgcd(b,a%b,y,x);
y-=(a/b)*x;return d;
}
int work(int m,int n,int x,vector<int> &G,vector<int> &B)
{
if(G.size()==m) return -1;//needn't to operate
int cnt=0,dis=1e18,ans=0;
for(int i:G) s[++cnt]=i*x%m,a[cnt]=i,p[cnt]=cnt;
for(int i:B) s[++cnt]=i*x%m,a[cnt]=i,p[cnt]=cnt;
sort(p+1,p+1+cnt,[](int i,int j)
{return s[i]==s[j]?i<j:s[i]<s[j];});//if s[i]==s[j],place boy back
s[p[0]=0]=s[p[cnt]]-m;s[p[cnt+1]=cnt+1]=s[p[1]]+m;//easy to calc dis
for(int i=1;i<=cnt;i++)//distance : under the circumstance of cirlces
dis=min(dis+n*(s[p[i]]-s[p[i-1]]),a[p[i]]);
for(int i=1;i<=cnt;i++)
{
dis=min(dis+n*(s[p[i]]-s[p[i-1]]),a[p[i]]);
if(s[p[i]]==s[p[i+1]]) continue;//not need to be considered
if(s[p[i]]+1==s[p[i+1]] && p[i]<=G.size()) continue;//girls born to be happy
ans=max(ans,dis+n*(s[p[i+1]]-s[p[i]]-1));//the last point of [s[p[i]],s[p[i+1]])
}
return ans;
}
signed main()
{
n=read();m=read();int x=0,y=0,d=0;
if((d=exgcd(n,m,x,y))>200000) Morisummer
for(int i=0,t,k=read();i<k;i++)
t=read(),A[t%d].pb(t/d);
for(int i=0,t,k=read();i<k;i++)
t=read(),B[t%d].pb(t/d);
x=(x%m+m)%m;y=(y%n+n)%n;
for(int i=0;i<d;i++)
{
if(A[i].empty() && B[i].empty()) Morisummer
ans=max(ans,work(m/d,n/d,x,B[i],A[i])*d+i);
ans=max(ans,work(n/d,m/d,y,A[i],B[i])*d+i);
}
printf("%lld\n",ans);
}




