[模板] 一般图最大匹配

一、题目

点此看题

二、解法

这里只讲算法流程，没有证明！没有证明！没有证明！

我们还是考虑沿用二分图匹配的思路：找增广路，我们循环 \(1\rightarrow n\) 找到一个没有匹配的点，然后尝试寻找它的匹配。我们以它为根对原图进行 \(\tt bfs\)，并且黑白交替染色，首先我们对根染黑色，然后对所有黑色点 \(u\) 访问 \(v\)：

• 如果 \(v\) 是一个没被访问过的点，考虑如果 \(v\) 没有被匹配那么我们就找到了增广路；如果 \(v\) 被匹配那么我们把 \(v\) 的匹配点染成黑色，并把它加入 \(\tt bfs\) 队列中。
• 如果 \(v\) 是一个被访问过的点，考虑如果 \(v\) 是白色，即表示 \((u,v)\) 在这棵 \(\tt bfs\) 树上构成了偶环，可以直接跳过；如果 \(u,v\) 已经在一个缩过的环中那么跳过；如果 \(v\) 是黑色，那么出现了奇环，带花树算法就是用来解决这个问题。

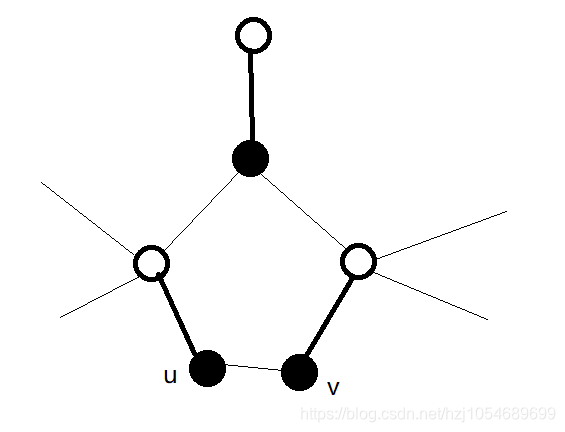
带花树算法描述的是，我们此时可以把奇环缩成一个点（称为缩花），那么如何缩点呢？考虑使用并查集，初始时每个点的奇环顶点都是自己。缩花的时候先用暴力 \(\tt lca\) 的方法找到环的顶点，我们直接将环上所有结点的父亲设置为这个顶点即可。

最后说一下实现中需要维护的重要数组及维护方法：

• \(fa[x]\)，表示 \(x\) 并查集的父亲，缩花的时候维护。
• \(mat[x]\)，表示 \(x\) 的匹配点，在找到增广路的时候修改。
• \(pre[x]\)，表示依据访问顺序白点 \(x\) 的上一个黑点，注意在缩花的时候需要把花上的 \(pre\) 都改成双向的，因为花是可以双向访问的。

时间复杂度我也不太清楚，但是我感觉是 \(O(|V|\cdot |E|)\) 的啊？

#include <cstdio>
#include <iostream>
using namespace std;
const int M = 1005;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,tim,tot,f[M];
int d[M],pre[M],mat[M],fa[M],bz[M],bp[M];
struct edge
{
	int v,next;
}e[M*M];
int find(int x)
{
	if(x!=fa[x]) fa[x]=find(fa[x]);
	return fa[x];
}
int lca(int x,int y)
{
	tim++;x=find(x);y=find(y);
	while(bp[x]!=tim)
	{
		bp[x]=tim;
		x=find(pre[mat[x]]);
		if(y) swap(x,y);
	}
	return x;
}
void make(int x,int y,int w)
{
	while(find(x)!=w)
	{
		pre[x]=y;y=mat[x];
		if(bz[y]==2) bz[y]=1,d[++d[0]]=y;
		if(find(x)==x) fa[x]=w;
		if(find(y)==y) fa[y]=w;
		x=pre[y];
	}
}
int bfs(int rt)
{
	for(int i=1;i<=n;i++) fa[i]=i,pre[i]=bz[i]=0;
	d[d[0]=1]=rt;bz[rt]=1;int l=0;
	while(l<d[0])
	{
		int u=d[++l];
		for(int i=f[u];i;i=e[i].next)
		{
			int v=e[i].v;
			if(find(u)==find(v) || bz[v]==2) continue;
			if(!bz[v])
			{
				bz[v]=2;pre[v]=u;
				if(!mat[v])
				{
					for(int x=v,y;x;x=y)
						y=mat[pre[x]],
						mat[x]=pre[x],
						mat[pre[x]]=x;
					return 1;
				}
				bz[mat[v]]=1;d[++d[0]]=mat[v];
			}
			else
			{
				int w=lca(u,v);
				make(u,v,w);
				make(v,u,w);
			}
		}
	}
	return 0;
}
signed main()
{
	n=read();m=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read();
		e[++tot]=edge{v,f[u]},f[u]=tot;
		e[++tot]=edge{u,f[v]},f[v]=tot;
	}
	int ans=0;
	for(int i=1;i<=n;i++) if(!mat[i])
		ans+=bfs(i);
	printf("%d\n",ans);
	for(int i=1;i<=n;i++) printf("%d ",mat[i]);
}