[提高组互测] Day2
总结
今天这一场得到了负分的好成绩,真的是最有教育意义的一场了。我花了一个小时打了 \(1,2,4\),然后花了两个半小时刚第三题获得了 \(20\) 分的好成绩,下次考虑每个题保证十分钟的检查时间,好对拍的题一定要对拍。
感谢 rainybunny 大佬的精心准备,以及模数 \(998244853\)(活久见),和她精心构造的大样例。原来无论我打出多少锅都可以过掉大样例,以后我出题也要给这样的大样例!!!
Fill The Bag
题目描述
解法
从低位到高位贪心,考虑如果不够用了就把最近的高位给分裂下来,如果当前位有多的那么直接合并上去。因为是按位贪心,并且每一次都是迫不得已的最优选择,所以感性上它是对的。
#include <cstdio>
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,ans,sum,b[100];
void work()
{
n=read();m=read();ans=sum=0;
for(int i=0;i<=60;i++) b[i]=0;
for(int i=1;i<=m;i++)
{
int x=read();sum+=x;
b[31-__builtin_clz(x)]++;
}
if(sum<n) {puts("-1");return ;}
for(int i=0;(1ll<<i)<=n;i++)
{
if(n&(1ll<<i))
{
if(b[i]) b[i]--;
else
{
int j=i;
while(!b[j]) b[j]++,j++,ans++;
b[j]--;
}
}
b[i+1]+=b[i]>>1;
}
printf("%lld\n",ans);
}
signed main()
{
int T=read();
while(T--) work();
}
Shake It!
题目描述
解法
考试的时候我把这题转成了树形结构,但和直接做本质是一样的,都是要找子问题,但本题的难点不是这东西
设 \(f[i][j]\) 表示 \(i\) 次加边操作,最小割为 \(j\) 的方案数,一次加边之后加上的两条边都是子问题,考虑这一小步时方案以 \(s\rightarrow t\) 的加边次数来区分,设 \(g[i][j]\) 表示上述状态加边一次的方案数:
定义后缀和状态 \(F[i][j]=\sum_{k\geq j}f[i][k],G[i][j]=\sum_{k\geq j} g[i][k]\),它们直接的转移枚举左边分配的加边次数和右边分配的加边次数即可,最小割就是左右两边的最小割取 \(\min\)(因为大路径就是这一条):
上述的过程可以结合下面的图来理解:
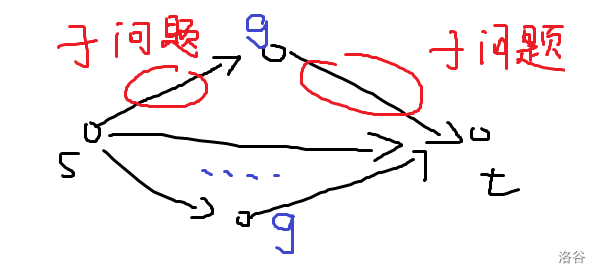
因为这一小步可能会被加边多次,所以我们要考虑 \(g\) 的"组合"。注意此时直接背包是不行的!注意到对于不同种类的 \(g\)(下标不同),它们对应的结构不同,但是同种 \(g\) 之间会存在相同的结构导致算重。
对于同种 \(g\),如果要从中选出 \(k\) 个来,问题转化成有 \(g[i][j]\) 个不同盒子,有 \(k\) 个相同小球,问可以空盒的放球方案数,那么显然是隔板法:\({g+k-1\choose k}\)
具体实现中,对于每一个新的 \(i\),我们计算出 \(g[i][j]\),然后考虑 \(g\) 对 \(f\) 的影响(枚举用多少、类似背包、复杂度调和级数),最后用 \(f\) 去计算 \(F\) 进入下一轮。时间复杂度 \(O(n^4\log n)\),卡上界就跑得飞快!
总结
结构观念真的很重要,本题很多结论就是我靠树形结构想通的(虽然题解里没有细讲)
无标号问题的计数,要考虑某种方案会不会因为同构的子问题被统计多次!去重方法可以转盒子放球模型。
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 105;
const int MOD = 1e9+7;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,f[M][M],g[M][M],h[M][M],inv[M];
void init(int n)
{
inv[0]=inv[1]=1;
for(int i=2;i<=n;i++)
inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
for(int i=1;i<=n;i++)
inv[i]=inv[i-1]*inv[i]%MOD;
}
void add(int &x,int y) {x=(x+y)%MOD;}
signed main()
{
n=read();m=read();init(100);
f[0][1]=h[0][0]=1;
for(int i=1;i<=n;i++)
{
//work for G
for(int j=1;j<=i+1;j++)
for(int k=0;k<i;k++)
add(g[i][j],f[k][j]*f[i-k-1][j]);
//work for f
for(int j=1;j<=i+1;j++)
for(int a=n;a>=0;a--)
for(int b=n;b>=0;b--)
{
int gg=(g[i][j]-g[i][j+1]+MOD)%MOD,tmp=0;
for(int si=0,sj=0,up=1,k=0;si<=a
&& sj<=b;si+=i,sj+=j,k++)
{
add(tmp,h[a-si][b-sj]*inv[k]%MOD*up);
up=up*(k+gg)%MOD;
}
h[a][b]=tmp;
}
//work for F
for(int j=i+1;j>=1;j--)
f[i][j]=(f[i][j+1]+h[i][j-1])%MOD;
}
int ans=(f[n][m]-f[n][m+1]+MOD)%MOD;
printf("%lld\n",ans);
}




