「LibreOJ β Round #3」绯色 IOI（危机）

一、题目

点此看题

二、解法

注意题目给了你两个特殊性质，要不然根本就做不了。

第一个性质的意思是，如果 \(u\) 能引爆 \(v\) 我们连有向边 \((u,v)\)，那么会得到一个 \(\tt DAG\)

第二个性质可以画图考虑性质，考虑 \(x_i<x_j<x_k\) 的三个点构成的图如下所示：

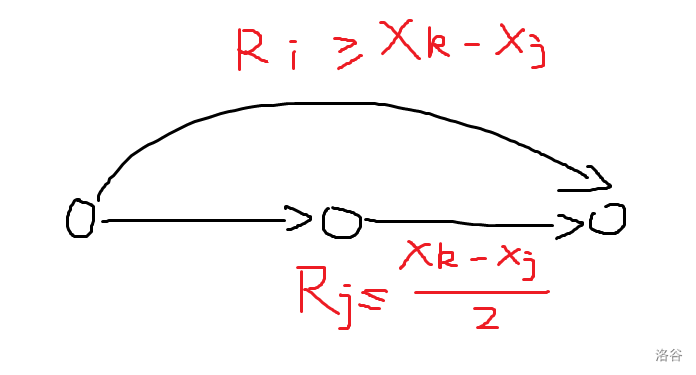
不难发现半径至少减少一半，所以最长的“引爆路径”长度为 \(\log n\) 级别。这可以推出能引爆某个炸弹的炸弹数量不超过 \(\log n\) 级别，所以我们只需要快速找到炸弹就可以暴力 \(dp\) 了。

但凡带点脑子都不会写线段树优化建图，其实有更好的方法。考虑只保留 \(d(i,j)=2\) 的边，那么拓扑图会被简化很多，而且新图上的拓扑关系是不变的，可以直接暴力 \(\tt dfs\)

对于每个点 \(j\) 最多存在两个这样的 \(i\)，考虑 \(x_j<x_k<x_i\) 的 \(j,k\) 都能到达 \(i\)，因为 \(j\) 一定能到达 \(k\)，所以只会保留 \(k\) 到 \(i\) 的边。单调栈二分找一下即可，时间复杂度 \(O(n\log n)\)

三、总结

当转移代价根本无法优化时，考虑快速找所有可能的转移点暴力转移。

复杂拓扑图的简化是个有趣的问题，很多题用各种方法都想达到去除无效边的目的。

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 300005;
const int MOD = 998244353;
#define int long long
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,rt,a[M],b[M],c[M],d[M],s[M],w[M],ch[M][2],dp[M];
int cmp1(int x,int y)
{
	return a[x]<a[y]; 
}
int cmp2(int x,int y)
{
	return b[x]>b[y];
}
void dfs(int u)
{
	if(!u) return ;
	int vl=((c[u]^c[rt])+c[u]*c[rt])%MOD;
	if(u!=rt) dp[rt]=max(dp[rt],dp[u]+vl);
	dfs(ch[u][0]);
	dfs(ch[u][1]);
}
signed main()
{
	n=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=n;i++) b[i]=read();
	for(int i=1;i<=n;i++) c[i]=read(),d[i]=i;
	//left
	sort(d+1,d+1+n,cmp1);
	for(int i=1;i<=n;i++) w[i]=a[i]+b[i];
	for(int i=1;i<=n;i++)
	{
		int x=d[i],l=1,r=m,t=0;
		while(l<=r)
		{
			int mid=(l+r)>>1;
			if(w[s[mid]]>=a[x])
				l=mid+1,t=s[mid];
			else r=mid-1;
		}
		ch[x][0]=t;
		while(m && w[s[m]]<=w[x]) m--;
		s[++m]=x;
	}
	m=0;
	for(int i=1;i<=n;i++) w[i]=a[i]-b[i];
	for(int i=n;i>=1;i--)
	{
		int x=d[i],l=1,r=m,t=0;
		while(l<=r)
		{
			int mid=(l+r)>>1;
			if(w[s[mid]]<=a[x])
				l=mid+1,t=s[mid];
			else r=mid-1;
		}
		ch[x][1]=t;
		while(m && w[s[m]]>=w[x]) m--;
		s[++m]=x;
	}
	sort(d+1,d+1+n,cmp2);
	for(int i=1;i<=n;i++)
		rt=d[i],dfs(rt);
	for(int i=1;i<=n;i++)
		printf("%lld\n",dp[i]);
}