CF1558E Down Below

一、题目

点此看题

二、解法

果然是 \(\tt tourist\) 搞的神题，很有启发意义。

首先这种经过每个点只有一次贡献的题，要么贪心要么网络流，\(dp\) 是难以解决的。

可以用类似增广的思路，也就是我们维护一个连通块，每次向连通块内加入一条从连通块出发，再回到连通块的增广路径，如果最后所有点都在连通块内那么就完成了增广。

但是这样做有后效性吗？考虑不能移动到上一个点的限制，由于增广之后上一个点是原先不在连通块内部的点，所以下一次增广一定可以从任意节点出发，并且上一个点是连通块内部的点，那么这个贪心一定没有后效性。

因为 \(b\) 全为正所以随便找一条路径增广即可，现在的问题是找增广路，有一个 \(\tt naive\) 的想法是直接 \(\tt dfs\)，如果 \(\tt dfs\) 到了一个访问过的点就找到了增广路径（为了保证复杂度没有必要 \(\tt dfs\) 时回到连通块），但是会有下面一种特殊情况：

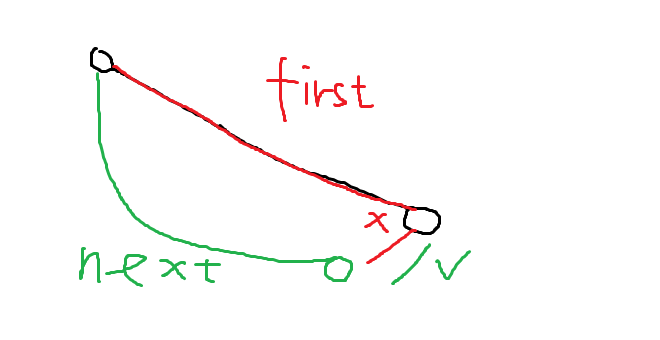
也就是我们先走红色的路径，但是因为 \(a_v\) 过大所以走不到绿色点，但是先走绿色路径却能先走到红色点。这种情况也是可以处理的，虽然 \(\tt dfs\) 的时候先走的红色路径，但实际上我们会先走 \(\sum b\) 大的那条路径。

最外面需要套个二分，时间复杂度 \(O(nm\log a)\)

三、总结

难以记录状态的图论题可以考虑增广的思路，连通图的耳分解也是类似增广的思路。

如何去除贪心的后效性是个问题，感觉本题的这个方法有点构造的意思

#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
using namespace std;
const int M = 1005;
const int inf = 0x3f3f3f3f;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int T,n,m,ans,a[M],b[M],vis[M],cur[M],pre[M];
vector<int> g[M];
int path(int x)
{
	if(vis[x]) return 0;vis[x]=1;
	return min(inf,path(pre[x])+b[x]);
}
int dfs(int u,int x)
{
	x=min(inf,x+b[u]);
	cur[u]=1;
	for(auto v:g[u])
	{
		if(v==pre[u] || x<=a[v]) continue;
		if(cur[v]) return path(u)+path(v);
		pre[v]=u;int f=dfs(v,x);
		if(f!=-1) return f;
	}
	return -1;
}
int check(int x)
{
	int f=0;
	memset(vis,0,sizeof vis);
	vis[1]=1;
	while(f!=-1)
	{
		f=-1;
		memcpy(cur,vis,sizeof cur);
		for(int u=1;u<=n && f==-1;u++) if(vis[u])
			for(auto v:g[u]) if(!vis[v] && x>a[v])
			{
				pre[v]=u;f=dfs(v,x);
				if(f!=-1) break;
			}
		if(f==-1)
		{
			for(int i=1;i<=n;i++)
				if(!vis[i]) return 0;
			return 1;
		}
		x=min(inf,x+f);
	}
	return 0;
}
void dich(int l,int r)
{
	if(l>r) return ;
	int mid=(l+r)>>1;
	if(check(mid))
	{
		ans=mid;
		dich(l,mid-1);
	}
	else dich(mid+1,r);
}
void work()
{
	n=read();m=read();
	for(int i=1;i<=n;i++) g[i].clear(); 
	for(int i=2;i<=n;i++) a[i]=read();
	for(int i=2;i<=n;i++) b[i]=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read();
		g[u].push_back(v);
		g[v].push_back(u);
	}
	dich(0,inf);
	printf("%d\n",ans);
}
signed main()
{
	T=read();
	while(T--) work();
}