CF573D Bear and Cavalry
一、题目
二、解法
首先根据农民伯伯都会的排序不等式(因为他们知道把最好的菜种进最好的地里),贪心策略是把人和马都按照权值大小排序,然后对应位相乘求和就行了,不难证明这是最优的匹配方案。
但是因为本题有第 \(i\) 个人不能和第 \(i\) 匹马配对的限制,所以说不一定取得到最优方案。这时候我想反悔贪心但是贪不出来(可能不适用,因为本题是最优解取不到的情况),但是考虑这个限制不是很多,可以往结论方向想。
感觉上和每个人匹配的马和它相差的位置不会太远,可以往匹配距离较小这个方向想。结论:不存在 \((i,i\pm 3)\) 这样的匹配,可以考虑反证\(+\)调整法,先假设会出现这样的情况,设 \(i\) 的禁止匹配位置为 \(ban[i]\):
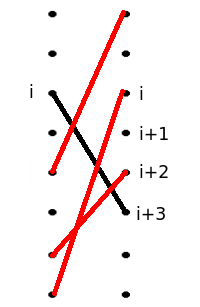
因为要完美匹配,所以至少会有三条红线和黑线相交。利用调整法不难证明如果两条线相交那么交换这两个匹配会得到更优的解,我们要考虑的是这样交换是否合法。注意到红线终点至多有一个是 \(ban[i]\),红线起点至多有一个的 \(ban=i+3\),就算是这样剩下的那一个就会合法,可以和它调整,那么这不是最优解,所以不存在 \((i,i\pm3)\) 的匹配。
然后考虑用 \(dp\) 解决问题,推论:如果只考虑前 \(i\) 个位置的匹配,那么只有可能 \([i-k,i]\ \ \ 0\leq k\leq 2\) 内部匹配然后得到子问题。设 \(f_i\) 为前 \(i\) 个位置匹配的最优解,那么转移:
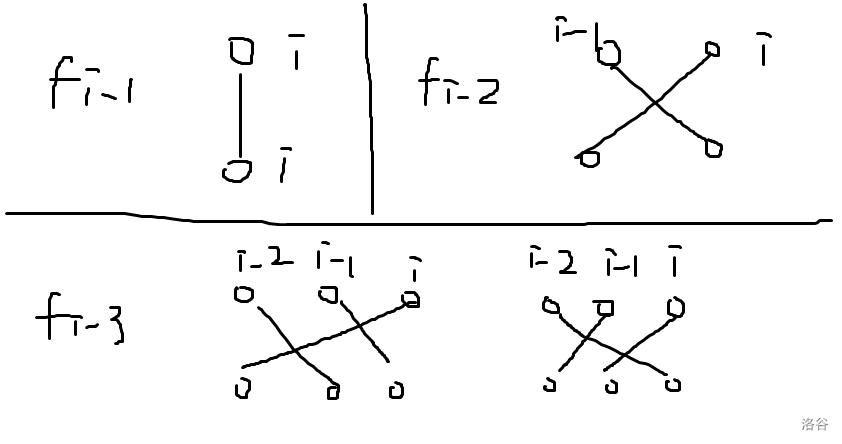
因为本题带修,所以把转移写成矩阵然后跑动态 \(dp\) 即可,时间复杂度 \(O(n\log n\cdot 3^3)\)
三、总结
转化到一定程度了可以猜一猜结论,可以靠一点感觉。
当限制条件不多时(比如本题只限制了某人不能匹配某马),那么可以强行摆脱限制(比如本题证明是跨越三个点那么怎么限制都阻止不了你调整),调整法是很重要的思维方式。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define int long long
const int M = 30005;
const int inf = 0x3f3f3f3f3f3f3f3f;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,a[M],b[M],p1[M],p2[M],ban[M];
struct node
{
int x,id;
bool operator < (const node &b) const
{
return x<b.x;
}
}s[M],t[M];
struct mat
{
int a[3][3];
mat() {memset(a,-0x3f,sizeof a);}
mat operator * (const mat &b) const
{
mat r;
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
for(int k=0;k<3;k++)
r.a[i][k]=max(r.a[i][k],a[i][j]+b.a[j][k]);
return r;
}
}tr[4*M];
mat con(int x)
{
mat r;
r.a[1][0]=r.a[2][1]=0;
r.a[0][0]=(ban[x]!=x)?a[x]*b[x]:-inf;
if(x<=1) return r;
r.a[0][1]=(ban[x]!=x-1 && ban[x-1]!=x)
?a[x-1]*b[x]+a[x]*b[x-1]:-inf;
if(x<=2) return r;
int c1=(ban[x]!=x-2 && ban[x-1]!=x && ban[x-2]!=x-1)
?a[x]*b[x-2]+a[x-1]*b[x]+a[x-2]*b[x-1]:-inf;
int c2=(ban[x]!=x-1 && ban[x-1]!=x-2 && ban[x-2]!=x)
?a[x]*b[x-1]+a[x-1]*b[x-2]+a[x-2]*b[x]:-inf;
r.a[0][2]=max(c1,c2);
return r;
}
void ins(int i,int l,int r,int id)
{
if(l==r)
{
tr[i]=con(l);
return ;
}
int mid=(l+r)>>1;
if(mid>=id) ins(i<<1,l,mid,id);
else ins(i<<1|1,mid+1,r,id);
tr[i]=tr[i<<1|1]*tr[i<<1];//attention
}
signed main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
s[i].x=read(),s[i].id=i;
for(int i=1;i<=n;i++)
t[i].x=read(),t[i].id=i;
sort(s+1,s+1+n);
sort(t+1,t+1+n);
for(int i=1;i<=n;i++)
{
a[i]=s[i].x;b[i]=t[i].x;
p1[s[i].id]=i,p2[t[i].id]=i;
}
for(int i=1;i<=n;i++)
ban[p1[i]]=p2[i];
for(int i=1;i<=n;i++)
ins(1,1,n,i);
while(m--)
{
int x=p1[read()],y=p1[read()];
swap(ban[x],ban[y]);
for(int i=max(1ll,x-2);i<=min(n,x+2);i++)
ins(1,1,n,i);
for(int i=max(1ll,y-2);i<=min(n,y+2);i++)
ins(1,1,n,i);
printf("%lld\n",tr[1].a[0][0]);
}
}



