[学习笔记] 长链剖分
不懂的东西就要来学啦!
简介
它和轻重链剖分区别就是重儿子的定义从所在子树最大的儿子变成了所在子树最深的儿子。
所以我们可以知道他主要用来解决和深度有关的问题,在优化 \(dp\) 方面应用十分广泛,但是它十分灵活,所以一定要练题。
性质
性质1
所有链长度的和是 \(O(n)\) 级别的。
性质2
任意一个点的 \(k\) 次祖先 \(y\) 所在的长链的长度大于等于 \(k\)
性质3
任何一个点向上跳越重链的次数不会超过 \(\sqrt n\) 次
懒得证了,上面的性质一个比一个显然 \(...\)
应用
一、计算k次祖先
这个一定要强烈推荐这位巨佬的题解,竟然把我讲懂了!
先预处理这些东西:
- 对树长链剖分,记录每个点的链头和深度,\(O(n)\)
- 倍增处理每个点的 \(2^n\) 次祖先,\(O(n\log n)\)
- 如果某条链的长度是 \(len\),那么记录链头向上的 \(len\) 个祖先和向下的 \(len\) 个链的元素,\(O(n)\)
- 记录每个数的二进制最高位 \(1\),\(O(n)\)
算法过程是这样的:
- 先利用倍增数组跳 \(k\) 的最高位,设剩余步数为 \(k'\),则 \(k'<\frac{k}{2}<\) 跳的步数
- 根据结论:
任意一个点的k次祖先y所在的长链的长度大于等于k,那么现在所处点的长链长度一定\(\geq\)跳的步数 \(>k'\),然后就可以用预处理出来的向上或者向下的数组 \(O(1)\) 获得 \(k\) 级祖先。
复杂度瓶颈是预处理 \(O(n\log n)\),但是单次询问只需要 \(O(1)\)
二、优化dp
就结合这个例题来讲把:Hotels
先考虑这三个点的位置关系,我们考虑答案可能是这个样子的,树上问题可以在 \(lca\) 处统计答案:
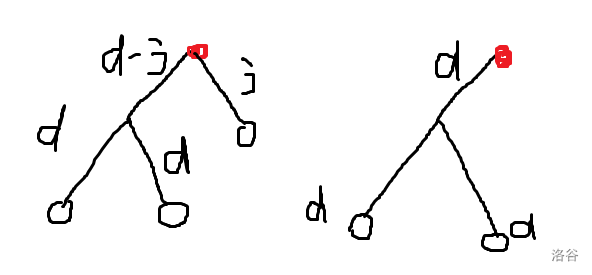
那么用 \(dp\) 来统计这些情况,设 \(f(i,j)\) 表示 \(i\) 子树以内深度为 \(j\) 点的个数,\(g(i,j)\) 表示 \(i\) 子树以内满足 \(d(lca(x,y),x)=d(lca(x,y),y)=d(lca(x,y),i)+j\) 的无序数对 \((i,j)\) 的个数,那么答案就这么统计:
-
\(ans\leftarrow g(i,0)\),对应了第二种情况。
-
\(ans\leftarrow \sum_{x\not=y} f(x,j-1)g(y,j+1)\)
我觉得应该是这么转移的,按照定义来就行了:
- \(g(i,j)\leftarrow \sum_{x<y} f(x,j-1)f(y,j-1)\)
- \(g(i,j)\leftarrow\sum g(x,j+1)\)
- \(f(i,j)\leftarrow\sum f(i,j-1)\)
暴力转移是 \(O(n^2)\) 的,但是发现下标都只和深度有关,所以可以用长链剖分优化。复杂度证明很巧妙,由于我们直接继承了重儿子的 \(dp\) 值,暴力加入轻儿子,复杂度消耗就是轻链的深度,由于每条链只会被加入一次,根据性质 \(1\) 链总长 \(O(n)\),那么时间复杂度 \(O(n)\)
写长链剖分的一个难点是继承重儿子的信息,需要用指针维护,用指针去分一个大数组就可以了,为了防 \(\tt RE\) 可以多安排一点空间。
#include <cstdio>
const int M = 100005;
#define int long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,tot,F[M],d[M],dep[M],son[M];
int *f[M],*g[M],p[4*M],*o=p,ans;
struct edge
{
int v,next;
edge(int V=0,int N=0) : v(V) , next(N) {}
}e[2*M];
void pre(int u,int fa)
{
d[u]=d[fa]+1;
for(int i=F[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa) continue;
pre(v,u);
if(dep[v]>dep[son[u]]) son[u]=v;
}
dep[u]=dep[son[u]]+1;
}
void dfs(int u,int fa)
{
if(son[u])//先访问重儿子
{
f[son[u]]=f[u]+1,g[son[u]]=g[u]-1;
dfs(son[u],u);
}
f[u][0]=1;
ans+=g[u][0];//经过其他儿子的 g[u][0] 会在下面 j=1 时统计
for(int i=F[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa || v==son[u]) continue;
f[v]=o;o+=dep[v]*2;g[v]=o;o+=dep[v]*2;
dfs(v,u);
for(int j=0;j<dep[v];j++)
{
if(j) ans+=f[u][j-1]*g[v][j];
ans+=g[u][j+1]*f[v][j];
}
for(int j=0;j<dep[v];j++)
{
g[u][j+1]+=f[v][j]*f[u][j+1];
if(j) g[u][j-1]+=g[v][j];
f[u][j+1]+=f[v][j];
}
}
}
signed main()
{
n=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
e[++tot]=edge(v,F[u]),F[u]=tot;
e[++tot]=edge(u,F[v]),F[v]=tot;
}
pre(1,0);
f[1]=o;o+=dep[1]*2;g[1]=o;o+=dep[1]*2;
dfs(1,0);
printf("%lld\n",ans);
}
三、奇怪的应用?
有时间了再看,\(yyb\) 博客上的




