[正睿集训2021] 概率与期望
前置知识
期望的线性性
第一个性质是期望的可加性:
第二个性质是当随机变量 \(X\) 和 \(Y\) 独立时:
条件概率
在 \(B\) 成立的前提下 \(A\) 成立的概率等于 \(AB\) 同时成立的概率除以 \(B\) 成立的概率:
贝叶斯公式同理:
\(%\)$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$
方差相关
概率生成函数
对于任意取值在非负整数集上的离散随机变量 \(X\),他的概率生成函数为:
一些性质:
Game on Tree
题目描述
解法
可以考虑每个点对期望操作次数的贡献,一个点期望产生 \(1\) 的贡献,当且仅当它比它的祖先先被染色,这样的概率是 \(\frac{1}{dep_i}\),所以每个点贡献的期望是 \(\frac{1}{dep_i}\)
那么根据期望的线性性,答案就是 \(\sum \frac{1}{dep_i}\)
Forest game
题目描述
给定一棵 \(n\) 个节点的树,每次等概率选择一个点,删去它和所有和它相连的边,得分记为这个连通块大小,总得分为每次操作得分之和,求总得分的期望。
\(n\leq 100000\)
解法
好像每次的得分是连通块大小,这个贡献好像不是很好算。考虑把它拆成更小的贡献 ,考虑删去 \(u\) 点时 \(v\) 点对它有没有贡献,当且仅当 \(u\) 是 \((u,v)\) 路径上第一个被删去的节点,期望是 \(\frac{1}{dis(u,v)+1}\)
根据期望的线性性,答案是 \(\sum_u\sum_v\frac{1}{dis(u,v)+1}\)
这种树上路径问题就可以考虑点分治,但是这个题要把每个距离有多少个给算出来。对于分治中心,考虑每个子树的生成函数,我们把它们暴力求卷积即可,再减去子树内部自己的卷积就可以了。时间复杂度 \(O(n\log^2 n)\),\(\tt FFT\) 要打递归版本的。
#include <cstdio>
#include <iostream>
#include <cmath>
using namespace std;
const int M = 400005;
const int p = 1e9+7;
const double pi = acos(-1.0);
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,tot,len,up,rt,ans,sz;
int f[M],siz[M],mx[M],vis[M],rev[M];
struct edge
{
int v,next;
edge(int V=0,int N=0) : v(V) , next(N) {}
}e[2*M];
struct complex
{
double x,y;
complex() {}
complex(double X,double Y) : x(X) , y(Y) {}
complex operator + (const complex &R) const {return complex(x+R.x,y+R.y);}
complex operator - (const complex &R) const {return complex(x-R.x,y-R.y);}
complex operator * (const complex &R) const {return complex(x*R.x-y*R.y,x*R.y+y*R.x);}
}a[M];
void FFT(complex *a,int len,int fl)
{
for(int i=0;i<len;i++)
{
rev[i]=(rev[i>>1]>>1)|((i&1)*(len/2));
if(i<rev[i]) swap(a[i],a[rev[i]]);
}
for(int s=2;s<=len;s<<=1)
{
int t=s/2;complex w=complex(cos(2*pi/s),sin(2*pi/s)*fl);
for(int i=0;i<len;i+=s)
{
complex x=complex(1,0);
for(int j=0;j<t;j++,x=x*w)
{
complex fe=a[i+j],fo=a[i+j+t];
a[i+j]=fe+x*fo;
a[i+j+t]=fe-x*fo;
}
}
}
}
int jzm(int a,int b)
{
int r=1;
while(b>0)
{
if(b&1) r=1ll*r*a%p;
a=1ll*a*a%p;
b>>=1;
}
return r;
}
void find(int u,int fa,int sz)
{
siz[u]=1;mx[u]=0;
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa || vis[v]) continue;
find(v,u,sz);
siz[u]+=siz[v];
mx[u]=max(mx[u],siz[v]);
}
mx[u]=max(mx[u],sz-siz[u]);
if(mx[u]<mx[rt]) rt=u;
}
void dfs(int u,int fa,int d)
{
sz++;
a[d].x=a[d].x+1;up=max(up,d+1);
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa || vis[v]) continue;
dfs(v,u,d+1);
}
}
void work(int fl)
{
len=1;
while(len<2*up) len<<=1;
FFT(a,len,1);
for(int i=0;i<len;i++) a[i]=a[i]*a[i];
FFT(a,len,-1);
for(int i=0;i<len;i++)
{
ll tmp=(ll)(a[i].x/len+0.5);
tmp%=p;
ans=(ans+fl*tmp*jzm(i+1,p-2))%p;
a[i].x=a[i].y=0;
}
}
void solve(int u)
{
up=0;dfs(u,0,0);
work(1);
vis[u]=1;
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v;
if(vis[v]) continue;
up=sz=0;dfs(v,0,1);
work(-1);
rt=0;find(v,0,sz);
solve(rt);
}
}
signed main()
{
n=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
e[++tot]=edge(v,f[u]),f[u]=tot;
e[++tot]=edge(u,f[v]),f[v]=tot;
}
mx[0]=n;
find(1,0,n);
solve(rt);
ans=(ans+p)%p;
for(int i=1;i<=n;i++) ans=1ll*ans*i%p;
printf("%d\n",ans);
}
[CTSC2017] 游戏
题目描述
解法
暴力 \(dp\) 是很容易的,但是如果要涉及到修改我们就束手无策了。考虑一些已知的比赛信息会把原序列划分成若干个段 \([i,j)\),对于每个段的贡献是独立的,现在问题变成了算一段的贡献,可以考虑线段树维护之类的方法。
那么我们要维护的东西一定要是 支持快速合并的 ,并且还要 钦定两端的状态 ,分别维护概率和期望。设 \(P_{i,j}(x,y)\) 表示 \(i\) 局输赢状态 \(x\),\(j\) 局输赢状态 \(y\) 的概率,\(E_{i,j}(x,y)\) 表示 假定这种输赢状态为前提 下 \([i,j]\) 赢得的期望场数,\(pro[i][j][k]\) 表示 \(i-1\) 轮状态是 \(j\),\(i\) 轮状态是 \(k\) 的概率(其实就是题目给的概率数组),那么有如下转移:
上面的式子很好理解,就是枚举中间的输赢情况是什么然后合并。
上面式子的本质其实是条件概率的一个应用:\(E(A|B)=\frac{E(AB)}{P(B)}\),我们要求的是有假定前提的期望,但是分子算的是包含假定前提成立的期望,所以除以假定前提成立的概率就行,这里的假定前提就是 \(i,j\) 的输赢状态分别是 \(x,y\)
用线段树很容易维护上面那个东西,修改就维护一个 \(set\),找一下前驱后继随便改一改就行了。
矩形覆盖
题目描述
给定一个大小为 \(n\times m\) 的矩形,某一些格子上有物品,共有 \(k\) 个物品,现在等概率选一个子矩形,求子矩形内物品个数的方差期望。
\(n,m\leq 1e9,k\leq 1e5\)
解法
根据方差期望那套理论,我们分别求出 \(E(x)\) 和 \(E(x^2)\) 即可。
\(E(x)\) 比较好求,对于每一个点统计它的贡献,对于 \((x,y)\) 有 \(x\times (n-x+1)\times y\times(m-y+1)\)
\(E(x^2)\) 可以套路地考虑每一对点,统计包含它们的矩形的个数,可以考虑扫描线,分左上右下和右上左下两种情况讨论,然后离散化\(\tt + BIT\) 即可。相信你们都知道我的意思了
逃跑
题目描述
解法
还是求方差期望的题,按照套路我们将其转化为分别求 \(E(x)\) 和 \(E(x^2)\)
先考虑怎么求 \(E(x)\),设 \(f(i,j,k)\) 表示第 \(i\) 秒第一次 移动 \((j,k)\) 的概率,设 \(g(i,j,k)\) 表示第 \(i\) 秒 移动 \((j,k)\) 的概率, 注意上面的定义位置是相对的 。对于 \((0,0)\) 它的含义就变成了到达,所以答案是所有 \(f(i,j,k)\) 的和,\(g\) 可以较为容易地用 \(dp\) 求出。对于一个点 \((x,y)\) 我们单独用生成函数算他的 \(f\):
那么满足下列关系式,含义就是花了时间不移动(注意相对的概念哦):
\(\tt Therefore\),\(f\) 可以在 \(O(n^4)\) 的时间复杂度内求得(可以写一个暴力多项式除法)
现在考虑 \(E(x^2)\) 怎么求,按照套路我们要对每一对点算贡献。考虑用 \(dp\) 处理,下面的操作就真的是艺高人胆大了,设 \(h(i,j,k)\) 表示第 \(i\) 秒第一次走到了 \((a+j,b+k)\),之前已经到达了 \((a,b)\),对于所有位置 \((a,b)\) 的概率,显然把最后时刻所有位置的 \(h\) 求和就是答案。这个状态定义为什么牛逼呢?因为它省略了状态里需要枚举的 \((a,b)\),但令人惊奇的是这样还能转移!
转移就先枚举 \(a,b\),再枚举一个时刻 \(t\),那我们就让它在 \(t\) 时刻第一次走到 \((a,b)\),在剩下 \(i-t\) 时间内第一次走到 \((a+j,b+k)\)。但是这样显然会算错,因为可能在走到 \((a,b)\) 的时候已经走到 \((a+j,b+k)\) 了。枚举一个时刻 \(t\),\(h(t,-j,-k)\) 就是经过 \((a+j,b+k)\) 第一次走到 \((a,b)\) 的方案,然后再第一次走到 \((a+j,b+k)\)(这里的第一次指的是这次征程的第一次),那么汇总一下就这么转移:
前面那一项是个人就会优化,所以时间复杂度 \(O(n^4)\)
[CTSC2006] 歌唱王国
题目描述
解法
这种题一般有套路的:列方程解生成函数 ,设 \(f[i]\) 表示结束时长度是 \(i\) 的概率,\(g[i]\) 表示长度是 \(i\) 还没有结束的概率,设 \(F(x)\) 为 \(f[i]\) 的生成函数,\(G(x)\) 为 \(g[i]\) 的生成函数,现在的任务是列出方程。
首先根据定义有:\(f[i]=g[i-1]-g[i],f[0]=0,g[0]=1\),那么可以推出 \(F(x)=xG(x)-G(x)+1\)
还要有一个方程才行,考虑 \(f,g\) 之间的联系,我们必须列一个方程来表示 \(f,g\) 之间的相互转化,考虑在 \(g\) 后面直接加入牛头人的名字 \(A\),设牛头人的名字长度是 \(L\),但是要考虑一种情况,就是没有加到 \(L\) 就已经合法了,但这时候 \(f\) 的后缀一定是 \(A\) 的一个 \(\tt border\),建议结合图来理解这个方程怎么来的:
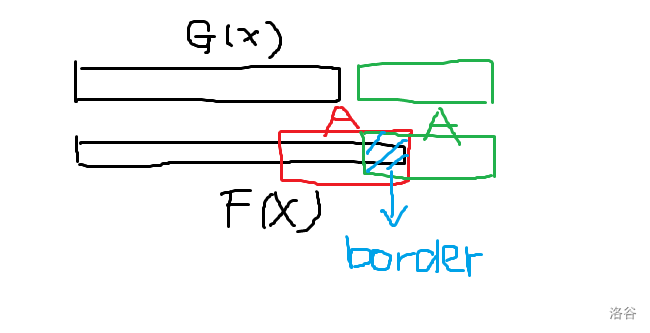
那么我们枚举 \(\tt border\) 的长度 \(i\) 就可以写出下列方程,注意我们列的是生成函数的方程,但原理是根据单个项的等式关系来的,所以要注意 对齐项数 ,设 \(a_i\) 表示 \([1,i]\) 是否是 \(A\) 的一个 \(\tt border\):
剩下的问题就是解方程了,由于求的是结束时间的期望那么答案是 \(F'(1)\),我们先把第一个方程求导:
然后将 \(x=1\) 带入上面的式子:
那么问题变成了求 \(G(1)\),尝试用第二个式子把 \(x=1\) 带进去:
大功告成啦!所以代码还需要我给么
Dice
题目描述
有一个 \(m\) 面的骰子,求扔连续 \(n\) 次就相同就结束的期望部分和扔连续 \(n\) 次结果不同就结束的期望步数。
\(n,m\leq 1e6\)
解法
解法只有一句话:照葫芦画瓢
第一问(注意第二个方程左边是一定成立的概率):
第二问:
如果你想从 \(n-1\) 来推也是可以的,只不过要注意去掉 \(g_0\) 那一项。
哥哥
懒得写了




