[正睿集训2021] 组合计数问题

Matrix-Tree定理

\(\tt UPD2022/1/28:\) 更正了一些错误，这么晚才修对不起了。

这里有一个极其简洁的证明，真的要模一下讲这次课的巨佬了。

\(\tt Matrix-Tree\) 定理本质上是对环容斥，容斥系数就是 \((-1)^{cnt}\) ，其中 \(cnt\) 表示除去自环的环个数。（自环代表容斥中的乱选，注意它是不贡献容斥系数的！！）

首先你要知道一个东西，奇排列表示交换奇数次得到 \(1,2,3...n\) 的排列，偶排列同理。那么奇排列的逆序对一定是奇数，偶排列的逆序对一定是偶数。这个有什么用呢？可以把交换次数的奇偶性转化成逆序对的奇偶性。

拿出置换环的那一套理论来把环放在我们的序列上，一个序列对应一个置换 \(p\) ，我们把 \(i\) 连向 \(p_i\) ，看形成了多少个环，这个环可以对应原图上的环，把这个序列的交换次数是 \(n-\)置换环个数。

然后考虑我们的基尔霍夫矩阵，对角线就表示随便选一条边，也就对应了容斥中的乱选，选 \((i,j)\) 就表示选 \(i\) 连 \(j\) 的一条边。由于求行列式自带的系数是 \((-1)^{tot}\) （表示逆序对），又有逆序对奇偶性等于 \(n-\)置换环个数的奇偶性，那么我们只需要把 \(i\not=j\) 的这些位置前面添一个负号，多了 \((-1)^{n-loop}\) 的系数（其中 \(loop\) 代表自环个数，注意不考虑乱选的东西哦），就可以得到 \((-1)^{cnt}\) 的容斥系数，这也印证了矩阵为什么要这么构造。

这个证明还可以用于矩阵树的有向扩展，如果你看懂了就没问题了。

所以怎么有向扩展呢？

热身题1

题目描述

有 \(n\) 堆石子，已知每堆石子的数量都介于 \([1,2^m-1]\) 之间且互不相同。给定 \(n,m\) ，求有多少种方案数使得 \(\tt nim\) 游戏下先手必胜。模 \(1e9+7\)

\(n\leq 1e7,m\leq30\)

解法

不妨考虑后手必胜怎么做，因为异或和为 \(0\) 要好做一些。

这道题有两个限制：石子数不为 \(0\) ，石子数互不相同。如果没了这些限制想想我们该怎么做，也就是乱选前面 \(n-1\) 堆，最后一堆就根据前面的异或和来选，就可以让异或和为 \(0\) 。

如果要求非 \(0\) ，可以考虑递推，设 \(f[i]\) 为 \(i\) 堆石子的答案，我们还是__让最后一堆石子去适应前面乱选的情况__，但是要求最后一堆石子不能是 \(0\) ，如果最后一堆石子是 \(0\) 那么以前的异或和一定是 \(0\) ，减去 \(f[i-1]\) 即可：

\[f[i]=(2^m-1)^{i-1}-f[i-1] \]

现在有要求互不相同，首先在乱选的方案上改一下，然后考虑最后一堆石子和别人相同的情况，先选出一个值和一个位置，使他们相同，剩下的 \(i-2\) 个数的异或和要是 \(0\) 才能让总体异或和是 \(0\) ，减掉这种方案：

\[f[i]=(2^m-1)(2^m-2)...(2^m-i+1)-f[i-1]-(2^m-1-i)(i-1)f[i-2] \]

然后暴力递推就可以了。

提问

这个 \(f[i-2]\) 我觉得是有点奇怪的，会不会撞到我们选出来的那个值从而多减呢？

我还不是很清楚。

这道题的思路是怎么来的？

就是先考虑简化的情况，再慢慢加入限制，我一开始总想着能不能直接计算，但是递推也是一种重要的方法。

热身题2

题目描述

给定 \(n\) 个正整数 \(a_i\) ，选出 \(n\) 个 \(b_i\) 和 \(d_i\) ，满足 \(b_i|a_i\) 且 \(d_i|b_i\) ，问有多少种选法可以满足 \(\prod d_i^2\geq\prod b_i\)

\(n\leq 100,a_i\leq 1e9\)

解法

一开始有一个特别巧妙的转化，这个大于等于是不好做的，考虑到如果 \(a\) 是 \(b\) 是因数，那么 \(b/a\) 也是 \(b\) 的因数。利用这个性质可以推出 \(\prod d_i^2>\prod b_i\) 和 \(\prod d_i^2<\prod b_i\) 是一一对应的。因为只用把 \(d_i\) 换成 \(b_i/d_i\) 就能转化成另一种不等关系，全部情况是比较好求的，那么减去 \(\prod d_i^2=\prod b_i\) 的情况就行了。

解决上面的问题可以分质因数做背包，然后把方案数乘起来（别看我，我没仔细想）

例1

题目描述

点此看题

解法

这么神的题我怎么做嘛

要把序列转化成环，这样原来 \(n\) 个位置就平等了 ，新建一个位置 \(n+1\) 表示如果有人选到了这个位置，就表示真实情况下他可能找不到位置。然后乱选的方案数是 \((2(n+1))^m\) ，考虑加入不能选 \(n+1\) 的限制，由于每个位置被选中的概率是一样的，所以有 \(\frac{m}{n+1}\) 的概率选到这个位置，那么不选到它的方案数是 \(\frac{m}{n+1}(2(n+1))^m\)

提问

为什么环上的点被选中的概率一样？

因为真实的座位选哪个和方向都是随便的，只有位置是不一样的。现在我们用环把位置这个限制都去掉了，环上是可以转的，所以是没有位置这个概念的，那么这些点被选中的概率就相等了。

思路怎么来的？

一开始那个变成环的操作我也没办法，但是核心思路是 把差别变成无差别 ，计算无差别是方便的。

例二

题目描述

点此看题

解法

看到这个组合数模 \(2\) 我就想到 \(\tt lucas\) 定理了，因为只有 \(C_{0,1}=0\) ，所以前面在二进制位上完全包含后面就行了，也就是后面是前面的子集。子集就很容易想到子集枚举，设 \(f[i]\) 表示以值 \(i\) 结尾的序列个数，不上升都不用管了，因为保证了子集也就保证了不上升。

然后枚举 \(i\) 的子集 \(j\) ，如果 \(j\) 对应的位置在 \(i\) 的前面的话就可以转移。这样复杂度做到了 \(O(3^{\log a})\) ，但是这种方法一定要求 值两两不同 这个条件才能保证复杂度。

提问

如果没有那个限制怎么做呢？我不是很懂。

例三

题目描述

求有多少个长度为 \(n\) 的括号序列满足其所有子序列中最长合法括号子序列长度为 \(2k\)

\(T,n\leq2e5,k\leq n\)

解法

括号序列问题一般把左括号看成 \(-1\) ，把右括号看成 \(1\)

这时候先把括号序列画在平面直角坐标系上，可以推一下最长合法括号子序列是多少。

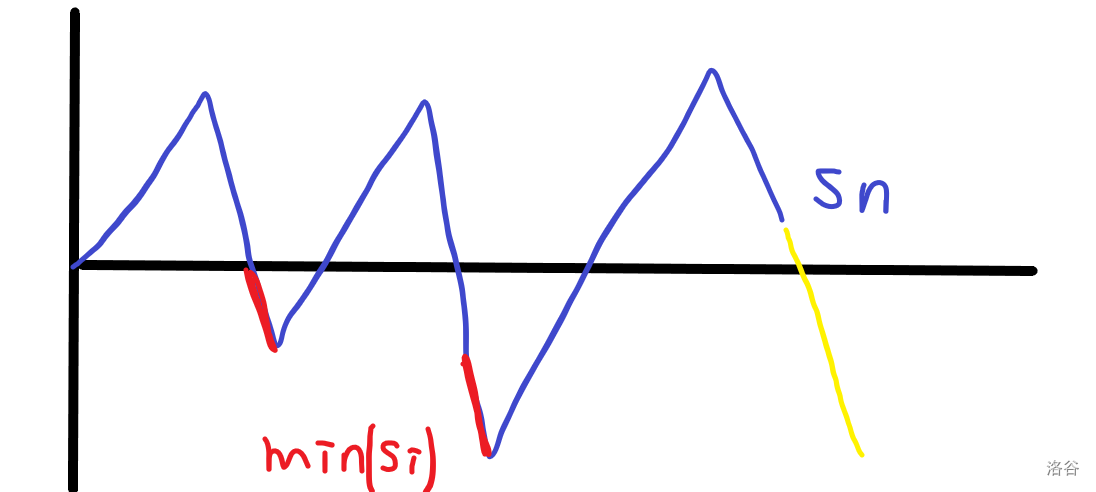
首先可以发现标红的部分是无法匹配的，那么错失匹配的右括号总数其实有 \(\min\{s_i\}\) 个，然后最后有 \(s_n-\min\{s_i\}\) 个左括号也无法匹配（对应标黄的部分），所以最长合法括号子序列个数是 \(n-s_n+2\min\{s_i\}\) 的。

枚举 \(t=\min\{s_i\}\) ，那么 \(s_n=n-2k+2t\)

算了不写了，这里开始就不懂了。

例四

题目描述

一棵树，每条边限制两个端点大小关系（\(a[u]>a[v]/a[u]<a[v]\)），问有多少种排列能满足整棵树的限制。

\(n\leq 5000\)

解法

规定一条边 \((u,v)\) 正向就表示 \(a[u]<a[v]\) ，那么如果所有的边都正向怎么做呢？拿出我们概率算方案数的那套理论，首先随便找一个排列，然后要满足的限制的就是每个子树内根是最小值，根成为最小值的概率是 \(\frac{1}{sz_i}\) ，那么考虑所有的限制，方案数就是：\(\frac{n!}{\prod sz_i}\)

然后现在引入了反向边，由于现在我们只能做正向边的情况，那么考虑一个容斥，我们枚举强制 \(i\) 条反向边正向。那么答案就是 零条边正向 \(-\) 一条边正向 \(+\) 两条边正向 \(....\) 的方案数。

除了强制的边其他反向边都是没有限制的，也就可以把这条边当作断开的，直接容斥复杂度 \(O(n2^n)\) 上天。

设 \(dp[u][i]\) 表示以 \(u\) 为子树的根 \(u\) 的联通块大小为 \(i\) 的容斥系数（最后乘 \(n!\) 就可以算答案），那么转移就类似于背包，要 考虑连向儿子的边断不断开 ，我觉得是这样转移的：

\[dp[u][i+j]-=dp[u][i]\times dp[v][j]\times\frac{i}{i+j} \]

\[dp[u][i]+=dp[u][i]\times dp[v][j] \]

如果这条边本身就是正向边那么这样转移：

\[dp[u][i+j]+=dp[u][i]\times dp[v][j]\times\frac{i}{i+j} \]

大概懂了，还有一点小问题

例五

题目描述

点此看题

解法

这道题就是上一道题的链版，但不好直接套，二维 \(dp\) 是不好优化的，我们尽量写成一维的形式。这道题做一维 \(dp\) 是比较简单的，设 \(g[i]\) 为考虑前 \(i\) 位的容斥系数，可以这样转移：

\[g[i]=\sum_{j=0}^{i-1}\frac{[s_j='>']}{(i-j)!}g[j](-1)^{cnt_{i-1}-cnt_j} \]

其中 \(cnt_x\) 表示 \(x\) 以内 > 符号的个数，也就是我们枚举第一个断开的是哪个。

容易发现上面的转移是分治 \(\tt NTT\) 的形式，那么不难做到 \(O(n\log^2n)\)

例六

题目描述

定义一个长度为 \(2n\) 的排列合法，当且仅当偶数位上的数字递增。把这个排列划分为恰好 \(k\) 个长度为偶数的段，这个划分的价值定义为所有段内逆序对个数的乘积。求随机排列和划分得到的价值期望。

\(n,k\leq 500\)

解法

我心态炸了

例七

题目描述

\(n\) 个点，第 \(i\) 个点到第 \(j\) 个点的有向边长度是 \(w[(j-i+n)\mod n]\) ，其中 \(w\) 是给定的数组，求所有内向生成森林的边权乘积之和。模 \(998244353\)

保证 \(n\) 是 \(2\) 的幂，\(n\leq 2^{20}\)

解法

哈哈，我不活啦

例八

题目描述

\(y\) 轴正半轴上有 \(n\) 个点 \((0,a_1)...(0,a_n)\) ，他们每次可以向右或者向下走一格，求最后分别到 \((1,0)...(n,0)\) 的方案数。

\[n,a_i\leq 1e6 \]

解法

其实这种题的难点主要是求行列式，矩阵通过 \(\tt LGV\) 引理是不难写出的：

\[\frac{1}{1!2!...n!}\begin{vmatrix}(a_1+1)^{\underline 1}&...&(a_1+n)^{\underline n}\\...&...&...\\(a_n+1)^{\underline 1}&...&(a_n+n)^{\underline n}\end{vmatrix} \]

然后做一些变换，首先提出公因式 \((a_i+1)\) ，那么矩阵就变成这样了：

\[\frac{\prod(a_i+1)}{1!2!...n!}\begin{vmatrix}1&...&(a_1+n)^{\underline {n-1}}\\...&...&...\\1&...&(a_n+n)^{\underline {n-1}}\end{vmatrix} \]

这里有一个套路，如果某一个矩阵的每行依次是关于 \(x\) 的 \(j-1\) 次多项式，那么这个矩阵是可以被消为范德蒙矩阵的。证明很简单，直接用前 \(j-1\) 列去消元 \(j\) 列即可，关键特征就是结构要相同，矩阵现在是这样的：

\[\frac{\prod(a_i+1)}{1!2!...n!}\begin{vmatrix}1&...&a_1^{n-1}\\...&...&...\\1&...&a_n^{n-1}\end{vmatrix} \]

利用一个范德蒙行列式的结论可以化简成这样（证明看百度百科，特别清楚）：

\[\frac{\prod(a_i+1)}{1!2!...n!}\prod_{1\leq j<i\leq n}(a_i-a_j) \]

统计 \(k=a_i-a_j\) 出现了多少次，因为值域很小，所以可以用卷积来统计，也就是这个卷积形式：

\[c_k=\sum g_i\times g_{i-k} \]

所以时间复杂度 \(O(a\log a)\)