[SNOI2019] 通信

一、题目

点此看题

二、解法

一看就是傻逼补流模型，不会真的有人这个图都建不出来吧

别走啊，我不阴阳怪气了，如果你不知道怎么建这里有图嘛（思路来源是餐巾计划问题）：

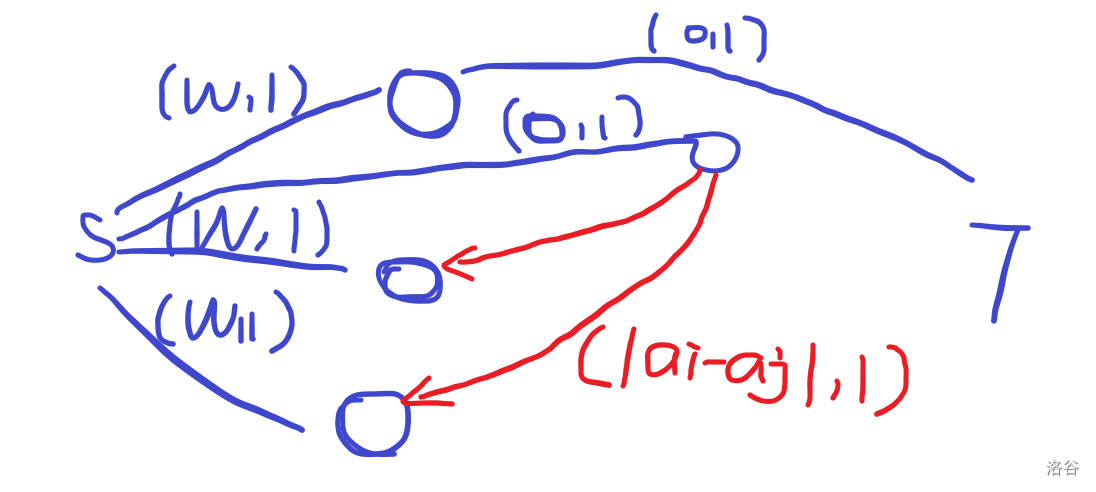
其中标红的边数量级很大，因为 \(i\) 点拆出来的点 \(i'\) 要连后面的每一个点 \(j\) ，边的数量达到了 \(n^2\) ，如果直接无脑暴力刚那肯定会吃 \(T\) 的，我测试过暴力跑的话只能得 \(80\) 分。

现在肯定要优化建图了，貌似可以可持久化权值线段树优化建图，因为 \(i<j\) 的每个点都要连所以建出后缀的权值线段树，然后分两部分连边。不过这里有一种小清新的做法，可以欣赏一下：

考虑类 \(\tt cdq\) 分治，每次考虑 \([l,mid]\) 连向 \([mid+1,r]\) 的边，可以把 \([l,r]\) 所有的权值取出来，每个权值都建一个虚点，排序之后相邻地连起来，容量为 \(inf\) 费用为权值之差。\([l,mid]\) 的点连向对应权值的虚点，对应权值的虚点连向 \([mid+1,r]\) 中的点，如果你觉得有点抽象这里还是有我精心（随便）绘制的图：

现在边数和点数都变成了 \(O(n\log n)\) ，所以没啥问题啦，如果你没写错是不会出现负环的。

因为我懒所以我写的第二种做法，但我坚信主席树是可以做到的：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int M = 100005;
#define int long long
const int inf = 1e18;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,w,tot,cnt,f[M],a[M],b[M],id[M];
int cost,s,t,dis[M],lst[M],pre[M],in[M],flow[M];
struct edge
{
	int v,f,c,next;
	edge(int V=0,int F=0,int C=0,int N=0) :
		v(V) , f(F) , c(C) , next(N) {}
}e[10*M];
void add(int u,int v,int c,int fl)
{
	e[++tot]=edge(v,fl,c,f[u]),f[u]=tot;
	e[++tot]=edge(u,0,-c,f[v]),f[v]=tot;
}
void cdq(int l,int r)
{
	if(l==r) return ;
	int mid=(l+r)>>1;
	cdq(l,mid);
	cdq(mid+1,r);
	//现在要考虑[l,mid]连到[mid+1,r]的边
	for(int i=l;i<=r;i++)
	{
		b[i]=a[i];
		id[i]=++cnt;//建虚点 
	}
	sort(b+l,b+r+1);
	for(int i=l;i<r;i++)
	{
		add(id[i+1],id[i],b[i+1]-b[i],inf); 
		add(id[i],id[i+1],b[i+1]-b[i],inf);
	} 
	for(int i=l;i<=r;i++)
	{
		int t=lower_bound(b+l,b+r+1,a[i])-b;
		if(i<=mid) add(i+n,id[t],0,1);
		else add(id[t],i,0,1);
	}
}
int bfs()
{
	queue<int> q;
	for(int i=0;i<=cnt;i++) dis[i]=inf;
	dis[s]=0;pre[s]=-1;flow[s]=inf;
	q.push(s);
	while(!q.empty())
	{
		int u=q.front();q.pop();
		in[u]=0;
		for(int i=f[u];i;i=e[i].next)
		{
			int v=e[i].v,c=e[i].c;
			if(dis[v]>dis[u]+c && e[i].f>0)
			{
				dis[v]=dis[u]+c;
				pre[v]=u;lst[v]=i;
				flow[v]=min(flow[u],e[i].f);
				if(!in[v]) in[v]=1,q.push(v);
			}
		}
	}
	return dis[t]<inf;
}
int Abs(int x)
{
	return x>0?x:-x;
}
signed main()
{
	n=read();w=read();
	s=0;cnt=t=2*n+1;tot=1;
	for(int i=1;i<=n;i++)
	{
		a[i]=read();
		add(s,i,w,1);
		add(i,t,0,1);
		add(s,i+n,0,1);
	}
	cdq(1,n);
	while(bfs())
	{
		cost+=dis[t]*flow[t];
		int zy=t;
		while(zy!=s)
		{
			e[lst[zy]].f-=flow[t];
			e[lst[zy]^1].f+=flow[t];
			zy=pre[zy];
		}
	}
	printf("%lld\n",cost);
}