[HNOI2014] 画框

一、题目

点此看题

二、解法

一看就知道是二分图匹配的题，但是这个总体不和谐度有点难啊。

我觉得 M_sea 讲的很好，这个貌似是一个计算几何的问题，定义一个点的坐标为 \((\sum x,\sum y)\) ，其实这个点就代表了一种匹配方案，那么他的横纵坐标相乘就代表了匹配方案的不和谐度，下面就是一些骚操作了：

找到一个离 \(y\) 轴最近的点 \(A\) ，找到一个离 \(x\) 轴最近的点 \(B\) （图我就直接嫖了啊） ：

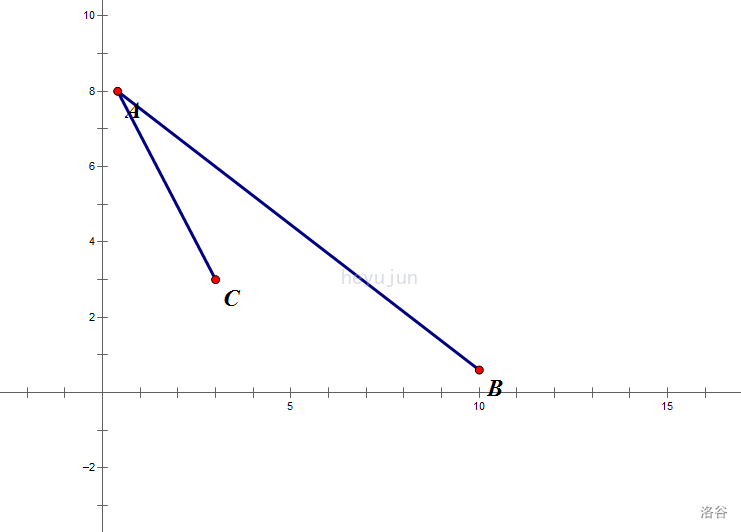
然后找到离线段 \(AB\) 最远的一个点 \(C\) ，也就是要求 \(S_{\Delta ABC}\) 的面积最大，用向量来表示就是 \(\frac{\vec{AB}\times \vec{AC}}{2}\) （叉积的物理意义就是向量围成三角形面积的两倍），我们把这两个向量平移到原点上，由于是顺时针旋转，所以叉积小于 \(0\) ，所以我们要让他最小，现在来推一下柿子啊：

\[\vec{AB}\times\vec{AC}=(x_B-x_A)\times(y_C-y_A)-(y_B-y_A)\times(x_C-x_A) \]

\[=(x_B-x_A)\times y_C+(y_A-y_B)\times x_C+y_Bx_A-x_By_A \]

所以我们要求 \((x_B-x_A)\times y_C\) 和 \((y_A-y_B)\times x_C\) 最小，我们把匹配的权值改成 \((x_B-x_A)\times b[i][j]+(y_A-y_B)\times a[i][j]\) ，然后用 \(\tt KM\) 跑最小权完美匹配就可以得到这个状态 \(C\) 点。

然后分治线段 \(AC\) 和 \(CB\) （也就是改变我们原来的 \(A,B\) 点递归下去），在分治的过程中用 \(C\) 点来更新答案即可。出口是 \(C\) 在 \(AB\) 上方，也就是 \(AB\) 和 \(AC\) 叉积为正（此时为逆时针），由于我还不会 \(\tt KM\) 所以暂时还没有代码。

有一个小疑惑啊，这个计算几何的方法应该是说 \(AC\) 和 \(CB\) 上方的点都不可能成为最优解的，那么如何证明呢？我还在想。