网络流简单题选做
简单一点的我就放这里了,难一点的题我会单独写题解的。
这是个好东西:https://www.cnblogs.com/victorique/p/8560656.html
还有一个好东西:https://www.cnblogs.com/Tiw-Air-OAO/p/14201641.html
网络流真的把我学爽了,我从没有学过这么有趣的东西,啊哈哈哈!!我没疯掉
有感而发,就总结在这里吧,有一类很重要的问题,规划来求最大权值网络流的做法。一般来说在题目中有意义的点连源点就表示选这种,连汇点就表示选那种,这些选择都是带权的,还是一些点的选择关系会产生权值:
- 第一种较简单的就是直接在有关系的两个点之间连边来表示权值:圈地计划
- 第二种就是权值关系比较复杂的话,还可以通过新建虚点,把权值放在这个点上:happiness
- 第三种就是边的权值不定,这时候或许可以通过解方程来求边的权值:Harmonious Army
[HEOI2016/TJOI2016]游戏
矩阵常常是网络流套路很多的地方,比如这道题我们用黑白染色之类的套路就做不了,因为他的限制主要在行列而不是图上的边相邻。我们先考虑只有软格子的情况,此时每一行或者每一列都只能选一个地方放炸弹。
这个放炸弹的过程可以看作行列匹配,可以这样建图:
- 源点连所有行,容量为 \(1\)
- 所有列连汇点,容量为 \(1\)
- 如果 \((x,y)\) 处是空地,那么把 \(x\) 行连到 \(y\) 列,表示这个点可以放炸弹,容量为 \(1\)
然后考虑硬格子带来的影响,它其实是把某一 行\(/\)列 割裂开来了,以他为分界的同一行其实可以看做两个独立的行,因为他们是互不影响的。然后我们把所有行列重新编号以后按简化版的思路来建图即可。
[SHOI2007]善意的投票
这道题可以用我们的惯用方法,先建出原问题的图论模型。假设 \((i,j)\) 两个人是好朋友,那么我们就把点 \(i\) 和点 \(j\) 连一条边,表示这两个人有选择一样的要求,然后我们在套上网络流来解决这个规划问题,最小冲突可以考虑求最小割:
- 源点连同意关灯的点 \(i\) ,权值为 \(1\) ,如果我们割去这条边表示 \(i\) 违背了他自己的意愿。
- 不同意关灯的点 \(i\) 连汇点,权值为 \(1\) ,如果我们割去这条边表示 \(i\) 违背了他自己的意愿。
- 对于原图上的连边 \((i,j)\) ,我们把他们之间连一条 双向边 ,权值为 \(1\) ,表示他们必须选同一个东西,否则我们必须通过割掉这条边来保证不连通性,正好累加了冲突,单向边的限制是不够的。
这个构图方法是我自己试出来的,更好的理解他呢,最重要的还是知道最后一个点要么和源点联通,要么和汇点联通,这个题要把边看成可以带来冲突的限制,解决的冲突的方法就是割掉这些边,所以可以把问题交给最小割。
[ZJOI2010]网络扩容
我差亿点就想到了。
可以搞一点正常的方法,我们把原图上的边看成费用为 \(0\) ,然后新建一些和原图重合的边,他们的费用为 \(w_i\) ,本题和费用流模型非常的契合,因为某条边多流 \(1\) 就要多花费 \(w_i\) 的费用。
但是这变得很不好控制,我们怎么让最大流刚好增加 \(k\) 呢?这时候 限流 的思想就很重要了,我们新建一个 \(n+1\) 点,让他连 \(n\) ,容量为最大流量\(+k\) ,费用是 \(0\) ,这样就达到了限流的效果,所以直接跑最小费用最大流即可。
[SDOI2010]星际竞速
据说是你谷比较难的网络流,我直接切了。
跟餐巾计划问题是一个样子的,本质都是补流模型,有时间了我再讲。
[AHOI2014/JSOI2014]支线剧情
这题太强了,但其本质还是 餐巾计划问题 。
我们考虑限制主要在边上面,所以我们把边拆成点 ,单独拿出来做。我一开始也是这么想的,但是这样构图有点麻烦,为了体现边的联系,我们 引入原图中的点 ,这样这就可以很好地把这些边串联起来。
每条边都要至少经过一次,所以我们让 \(1\) 单位流入汇点的流量代表这个限制。由于流入汇点这个操作会损失 \(1\) 单位流量,我们多建一个点,让源点把这个流量补回来,大致的网络雏形已经出来了,我们这样构图:
- 源点连剧情 \(1\) ,表示可以一直从剧情 \(1\) 开始走。
- 对于连接剧情 \(u,v\) 的边 \(i\)(拆成 \(i\) 和 \(i'\) ) ,我们把 \(u\) 连 \(i\) ,容量为无限,费用为边权,表示使用这条边;然后 \(i\) 连 \(i'\) 容量为无限,费用为 \(0\) ;\(i\) 连汇点,容量为 \(1\) ;源点连 \(i'\) ,容量为 \(1\) ;\(i'\) 连接剧情点 \(v\) ,容量无限。
图如果要画出来长这样(借用一下 JYU1020180213 大佬的图,侵删):
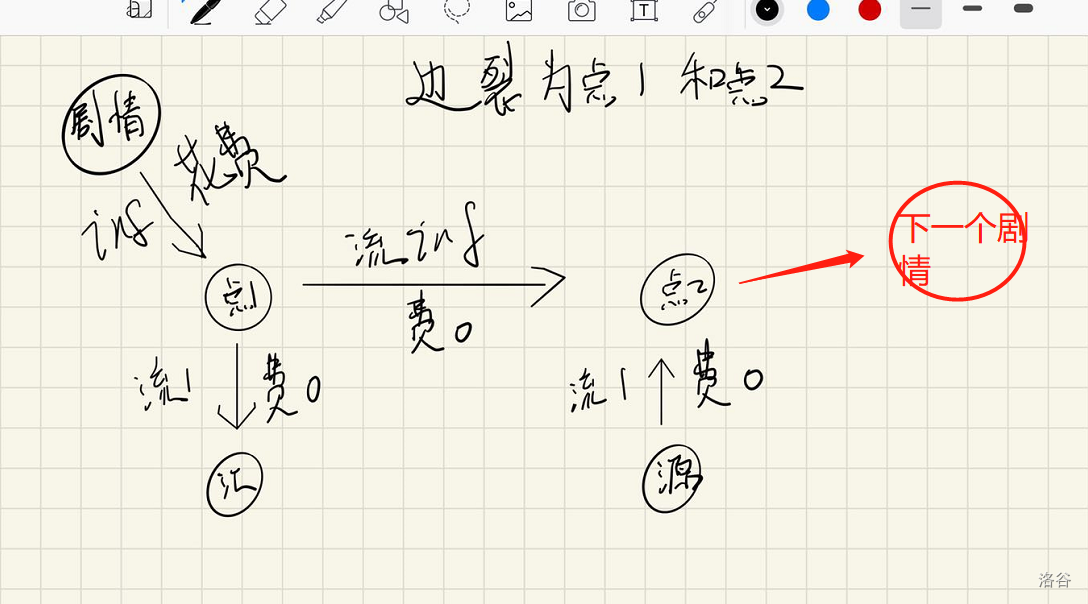
还有一种最小费用可行流的方法,以后填坑。
[NOI2008] 志愿者招募
题目描述
解法
这道题真的很特殊,和我做到的其他网络流都有较大的差别,这道题的流量是没有物理意义的,我愿称之为:无意义模型 ,或者从题目特性的角度,称之为:一面对多面模型
还是由这道题本身的特性决定的,网络流的流量通常只能单一配对,但是这道题的志愿者却能服务一个区间,这就给我们的建图造成了很大的麻烦。所以我们一开始二分图那种样式的网络流不管用了,我们尝试 按照时间顺序建图(依次满足每一天)
想象一开始我们有一个无意义的图,\(1-n+1\) 连接相邻两点的边容量都是 \(inf\) ,无费用,最大流是 \(inf\),源点连 \(1\) ,\(n+1\) 连汇点 。然后我们尝试加入每一天 \(a_i\) 个志愿者的限制条件,流量是没有意义的,我们尝试在边上面做文章。我们把 \((i,i+1)\) 的边的容量设置成 \(inf-a_i\) ,表示第 \(i\) 天要有 \(a_i\) 个志愿者。
但是现在最大流就不是 \(inf\) 了,我们要用到志愿者。志愿者 \((s_i,t_i,c_i)\) 其实就是能让 \([s_i,t_i]\) 这些天多流 \(1\) 的流量(因为我们要让最大流等于 \(inf\)),那么我们把 \(s_i\) 和 \(t_i+1\) 连一条容量无限,费用为 \(c_i\) 的边,表示这类的志愿者的功能,就是帮助这些天分担流量。
这个思路很神奇,我暂时没有想出比这更好的解释方法了。
[NOI2009] 植物大战僵尸
题目描述
解法
建议先做一下:太空飞行计划问题
考虑先建出本题的图论模型,发现本题其实就是一个保护关系,有两种连边方式:
- 如果 \((i,j)\) 能攻击 \((x,y)\) ,那么 \((i,j)\) 保护 \((x,y)\) ,\((i,j)\) 连向 \((x,y)\)
- 因为要先吃 \((i,j+1)\) 才能吃 \((i,j)\) ,\((i,j+1)\) 会保护 \((i,j)\) ,那么 \((i,j+1)\) 连向 \((i,j)\)
考虑先找出那些无论如何都不会被吃的节点,也就是 一个节点在某个环里面 或 一个节点被某个环保护着 ,所以我们可以对建出来的图跑拓扑排序,被拓扑到的点就是可能被选的点。
然后考虑一个点被选需要怎样,那么保护他的点就必须要被选。想选什么,就必须要选什么,这不是 最大权闭合子图 问题吗?可以把所有点分成正权点和负权点,然后用网络流解决:
- 源点连正权点,容量是权值。
- 负权点连汇点,容量是权值的绝对值。
- 如果 \((u,v)\) 在原图上有有向边,我们在网络流图上连 \((v,u)\) ,权值为 \(inf\) 。
答案是正权点权值和 \(-\) 最小割,好像必须要用当前弧优化。
最后补充一下,我看网上的题解的时候发现他们说建出网络流图之后对反图跑拓扑。但我认为的逻辑是:先建出原图跑拓扑,然后再建出网络流图(网络流图的边和原图的边方向是反的)
[NOI2012] 美食节
题目描述
解法
这种等待时间的问题用到了 费用提前计算 的思想。
也就是拆点,我们把每个厨师拆成做最后一道菜的厨师,做倒数第二道菜的厨师 \(...\) 做倒数第 \(i\) 道菜的厨师连所有菜,容量为 \(1\) ,边权为 \(i\space\times\) 做这道菜的时间,然后跑最小费用最大流。
但是这样暴力建图点数都有 \(O(mp)\) ,而且边也要连满,图都难以建出来。但是我们发现对于一个厨师,是做最后一道菜的他先被选,在可能取用另外的他,所以可以当前一个他被使用过以后,再建出后一个他。也就是 动态地建网络流图 。注意 \(\tt spfa\) 里面要加入队标记
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
const int M = 100005;
const int inf = 0x3f3f3f3f;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,cnt,tot,sum,ans,f[M],tm[45][105],zy[105];
int s,t,dis[M],pre[M],lst[M],flow[M],in[M],st[105];
struct edge
{
int v,f,c,next;
}e[100*M];
void add(int u,int v,int c,int fl)
{
e[++tot]=edge{v,fl,c,f[u]},f[u]=tot;
e[++tot]=edge{u,0,-c,f[v]},f[v]=tot;
}
void upd(int x,int k)//第x个厨师的第k个状态
{
++cnt;
add(s,cnt,0,1);
st[x]++;zy[x]=tot-1;//存下连向起点的边
for(int i=1;i<=n;i++)
add(cnt,i,k*tm[i][x],1);
}
int bfs()
{
queue<int> q;
for(int i=s;i<=cnt;i++) dis[i]=inf;
flow[s]=inf;dis[s]=0;pre[s]=-1;
q.push(s);
while(!q.empty())
{
int u=q.front();q.pop();
in[u]=0;//以后一定要写这个啊
for(int i=f[u];i;i=e[i].next)
{
int v=e[i].v,c=e[i].c;
if(dis[v]>dis[u]+c && e[i].f>0)
{
dis[v]=dis[u]+c;
flow[v]=min(flow[u],e[i].f);
pre[v]=u;lst[v]=i;
if(!in[v])
{
in[v]=1;
q.push(v);
}
}
}
}
return dis[t]<inf;
}
int main()
{
n=read();m=read();
cnt=n+2;s=0;t=n+1;tot=1;
for(int i=1;i<=n;i++)
{
int p=read();sum+=p;
add(i,t,0,p);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
tm[i][j]=read();
for(int i=1;i<=m;i++)
upd(i,1);
while(bfs())
{
sum-=flow[t];
ans+=flow[t]*dis[t];
int jzm=t;
while(jzm!=s)
{
e[lst[jzm]].f-=flow[t];
e[lst[jzm]^1].f+=flow[t];
jzm=pre[jzm];
}
for(int i=1;i<=m;i++)
if(e[zy[i]].f==0)//这条边被用了
upd(i,st[i]+1);
if(sum==0) break;
}
printf("%d\n",ans);
}
[CQOI2012]交换棋子
题目描述
解法
我认罪了,我以前一直瞧不起 \(\tt CQOI\) ,直到今天被这道题虐了。再也不敢瞧不起 \(\tt CQOI\) 了,我是弟弟。话说这个题很好啊,题目很简洁,做法很牛逼(我差点就想出来了,哎)
首先告诉你一个我都知道的东西:忽略原图中所在的白点,如果我们把黑点移动到了目标位置那么我们就成功了。为了严谨我再说明一点:最优情况下一定不会交换两个黑点,综上问题可以看成单个黑点的移动
有一个小细节就是如果起点和终点都在一个位置的黑色棋子需要忽略(看了建图方法你就知道为什么了)
所以可以把黑点当成流量,求出最大流时就对应了黑点归位。现在一个主要的问题是 \((i,j)\) 位置的格子只能进行 \(m_{i,j}\) 次交换,这个限制是在点上的 ,如果用网络中的边是无法表示这个限制的,所以我们要拆点,点 \(i\) 拆成 \(x_i\) 和 \(y_i\) ,用他们之间的连边来表示限制 ,然后因为要求交换次数最少所以可以跑最小费用流,到现在思路大概都出来了,这样建图哦:
- 对于初始状态有黑点的 \(i\) ,源点连 \(x_i\) ,容量为 \(1\) ,费用为 \(0\)
- 对于目标状态有黑点的 \(i\) ,\(y_i\) 连汇点,容量为 \(1\) ,费用为 \(0\)
- 对于八联通的两个格子 \(i,j\) ,\(y_i\) 连 \(x_j\) ,容量为 \(inf\) ,费用为 \(1\)
- 对于 \(x\) 向 \(y\) 连流量 \(m_{i,j}\div2\) ,费用为 \(0\) 的边,注意这里我们是两个愿望一次满足,也就是我们把换进来和换出去的操作同时做了,所以一个流量消耗为 \(2\) 。但是这个点还可能不换出去(或者不换进来),所以当 \(m_{i,j}\) 为奇数并且初始或者结束状态中有黑色格子的时候可以只消耗 \(1\) ,这时候多连 \(1\) 的流量。
突然想起来了,我没有写代码
[ZJOI2011]营救皮卡丘
题目描述
解法
其实这个题最难的是 因此,在K-1号据点被摧毁之前,任何人是不能够经过K号据点的。 这个限制特别操啊,本来想的是动态网络流,但是这个模型不满足不能贪心,然后我就挂在这个地方了。
其实还是对网络流的理解出了问题,比如说我们以为先流 1->3->5 再流 1->2->4 就是不合法的。但是在实际情况中完全可以第二个人先 1->2 第一个人再 1->3 然后 2->4,3->5 。也就是说网络流中是不存在所谓时间顺序的 ,知道这一点后你可以再想一想我们的限制条件变成了什么:因为每个点最后都会被流到,所以只要不通过编号大的点去解锁编号小的点就是合法的 。
注意这并不是说大编号到小编号的边就不能用了,解锁的意思是第一次流经这个点。这时候用原图中的边并不好做这个题,你怎么知道一个点解锁没解锁?我们知道流量的目的就是解锁点,所以我们让流量不通过原图的边,而是用直达的方式解锁点 。所以把原图上的边换成路径,用 \(\tt floyd\) 来做,每次 \(k\leq\max(i,j)\) 的时候才去松弛,这样就只用了编号小的点去解锁编号大的点。
然后就变成垃圾题了,就是一个补流模型,太熟练了不想讲了。
[WC2007]剪刀石头布
题目描述
给你一个竞赛图,其中有一些边已经确定方向,要求确定某些边的方向,最大化三元环个数。
解法
不用好题目中的条件就等着凉吧!本题最重要的条件其实是 竞赛图 ,他告诉我们三元环的充要条件是只考虑 \((A,B,C)\) 的情况下三个点入度出度都是 \(1\) ,不合法的情况也很唯一,就是一个点出度为 \(2\) ,一个点入度为 \(2\) ,一个点出度入度都为 \(1\) 。
我们不妨从入度的角度来考虑这个问题,就是考虑一个点对三元环的贡献 。如果一个点入度为 \(i\) ,那么从 \(i\) 中选两条边出来,可以不构成三元环,所以它的负贡献是 \(C_{i}^2\) ,一个点增加 \(1\) 的度数就会减少 \(C_i^2-C_{i-1}^2=i-1\) 个三元环。
剩下的问题就是规划度数了,可以用网络流,把为定向的边当成源点和有关点的边,容量为 \(1\) 费用为 \(0\) (所以这里我们的流量就代表了度数),然后每个点都向汇点连容量为 \(1\) ,费用为 \(0,1,2,3....\) 的边,这样就可以计算贡献了。最后跑最小费用最大流就得到了答案。
哎,一遇到有点思维难度的题我就想不出来,我是辣鸡
[北京省选集训2019]图的难题
题目描述
操哈哈哈,一开始把题读错了浪费好多时间想个错题
解法
拿到这道题有一个大概的想法,如果 \(E>2V-2\) 那么这个图就一定是不合法的。
但这只是个必要条件,如果 \(E\leq 2V-2\) 也有可能原图不合法,这时候我们就要略做改动,把必要条件变成充要条件 。
然后你要知道如果一个图的子图满足 \(E>2V-2\) ,那么这个图也是不合法的,因为子图中如果会出现环那么相当于原图会出现环。结论是:当前仅当对于任意一个导出子图,\(E\leq 2V-2\) 时合法。
略微变一下形 \(E-2V+2\leq 0\) ,所以找到最小的 \(E-2V+2\) 判断其正负就可以了。你发现边是正贡献,点是负贡献,从选边的角度来思考,主动选了边就一定要选对应的点,所以是 最大权闭合子图模型 。
具体来说我们把边看成点,从源点连一条流量为 \(1\) 的边过来。然后把边 \((u,v)\) 连向 \(u\) 和 \(v\) 容量为 \(inf\) ,点连汇点流量为 \(2\) ,然后求边数和\(-\)最小割就是答案(也就是正权点\(-\)最小割)




