符号规定
| \(\Omega\) |
模拟角频率 |
| \(\omega\) |
数字角频率 |
| \(T\) |
采样周期 |
| \(\Omega_{s}\) |
采样角频率 |
| \(\Omega_N\) |
连续信号最大角频率 |
连续信号的采样
对于一个连续信号\(x_{c}(t)\)，其经过冲击采样之后获得之后变成一个冲击串函数\(x_{s}(t)\)，即：
\[x_{s}(t) = \sum\limits_{n=-\infty}^{\infty}x_{c}(t)\delta(t-nT) =
\left \{
\begin{matrix} x_{c}(nT) &t=nT \\ 0 &其他 \end{matrix}
\right.
\]
显然，对于\(x_{s}(t)\)任然是一个连续信号，我们需要经过量化之后获得我们所需要的离散信号\(x[n]\)，有\(x[n] = x_{c}{nT}\)
流程如图：
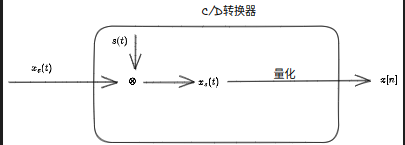
频域分析
对\(x_{s}(t)\)进行连续傅里叶变换有：
\[X_{s}(j\Omega) = \frac{1}{2\pi}X_{c}(j\Omega)*S(j\Omega)
\]
其中
\[S(j\Omega) = \frac{2\pi}{T}\sum\limits_{k=-\infty}^{\infty}\delta(\Omega-k\Omega_{s})
\]
所以有：
\[X_{s}(j\Omega) = \frac{1}{T}\sum\limits_{k=-\infty}^{\infty}X_{c}(j(\Omega-k\Omega_{s}))
\]
显然，采样后的频域是对原本连续信号频域的周期延拓，这里面要求有：
\[\Omega_{s} > 2\Omega_{N}
\]
这里\(\Omega_{N}\)称之为奈奎斯特频率，\(2\Omega_{N}\)称之为奈奎斯特率
在对\(x[n]\)进行DTFT，有：
\[X(e^{j\omega}) = \frac{1}{T} \sum\limits X[n]e^{-j\omega n}
\]
对比上述式子，有：
\[X_{s}({j\Omega}) = X(e^{j\omega})|_{\omega= \Omega T}
\]
所以上面冲击串函数的在数字频域上可以表示：
\[X_{s}(j\omega ) = \frac{1}{T}\sum\limits_{k=-\infty} ^{\infty}X_{c}(j(\frac{\omega}{T}-2\pi \frac{k}{T}))
\]
即对采样之后在数字角频域进行了归一化
例1
假设\(T=1/600\)，模拟连续信号\(x_{c}(t) = cos400\pi t\)
可以计算出：\(\Omega_{s}=1200\pi, \Omega_{N} = 800\pi\)
由时域采样定理知：可以用一组离散信号表示原连续信号
此时\(X_{s}(j\Omega)\)图像如下：
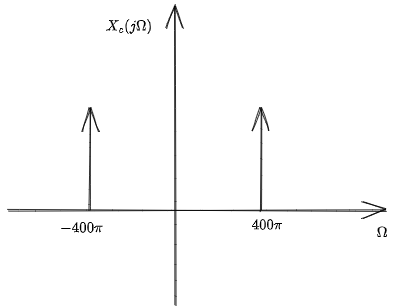
在进行归一化有：
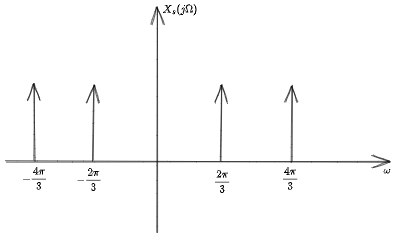
连续信号的复原
对于数字序列\(x[n]\)，我们可以构造一个连续的冲击串函数\(x_{s}{t}\)，有：
\[x_{s}(t) = \sum\limits_{n=-\infty}^{\infty}x[n]\delta(t-nT)
\]
对于这个函数，我们已知其在频域上等于原连续信号的周期延拓，所以我们希望使用一个低通滤波器对其进行滤波再添加一个T倍的增益，该门函数的截止频率一般取\(\Omega_N\)的一般。
对于截止频率为\(\Omega_{H}\)，频率增益为A的门函数，其时域形式为：
\[h(t) = \frac{1}{\pi}A\Omega_{H}sa(t\Omega_{H})
\]
所以有：
\[h_{r}(t) = sa(\frac{t\Omega_{N}}{2}) = \frac{\sin(\pi t/T)}{\pi t/T}
\]
所以在频域上将\(X_{s}(j\Omega)与H(j\Omega)\)相乘，在时域上表现为卷积，有：
\[x_{r}(t)= x_{s}(t)*h_{r}(t) = \sum\limits_{n=-\infty}^{\infty}x[n]h_{r}(t-nT) = \sum\limits_{n=-\infty}^{\infty}x[n]\frac{sin(\pi (\frac{t}{T}-n)}{\pi(\frac{t}{T}-n)}
\]
则可以抽象成一个D/C转换器
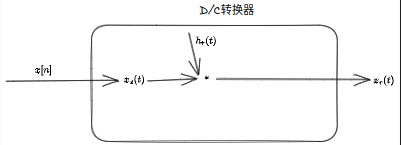
完整的步骤
时域连续信号在进过采样之后变成数字序列，而DSP处理的对象即为数字序列，经过输入到系统中后输入一个响应，将输出响应再进行复原成时域连续信号。
后面我们将围绕中间系统部分详细展开。
