并查集拓展——种类并查集&带权并查集

在所面临的问题中，我们不仅需要知道两个元素之间是否存在关系，还需要记录其他要素，于是我们需要对原来的并查集进行拓展。

种类并查集

对于一般的并查集，只能表示“朋友的朋友就是朋友这种关系”，即我们只关系元素之间的连通性问题。但是对于“敌人的敌人就是朋友”这种关系则无能为力。种类并查集就是为了解决这种问题，他将一个并查集变成原来的两倍大小，前一半用来维护朋友关系，后一半用来描述敌人关系。

具体步骤详解

创建

首先我们构建原来两倍大小的并查集
假设原来大小为4，现在构建一个长度为8的并查集，前4个表示朋友关系，后4个表示敌人关系。如1和5就是敌人，3和7就是敌人

连接

假设1 和 2之间是敌人关系，即2就和5是朋友关系（敌人的敌人就是朋友，2，5都是1的敌人），1和6就是朋友关系
再有1和3是敌人关系，则3和5就是朋友，1和7就是朋友。
如图：

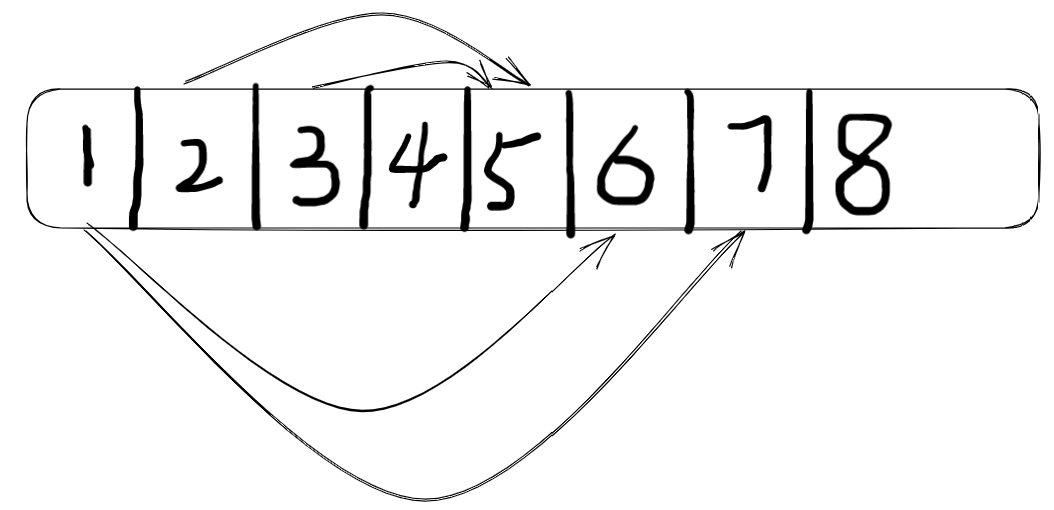
这样2和3这样的敌人的敌人就是朋友关系即可满足。

例题

logu P1892 团伙

原题链接
显然，题干直接描述的就是种类并查集，可以有代码：

#include <iostream>
using namespace std;
const int N = 10e5 + 10;
int tr[N];
void initial(int n) {
	for (int i = 1; i <= 2 * n; i++) tr[i] = i;
}
int find(int x) {
	if (x == tr[x]) return x;
	tr[x] = find(tr[x]);
	return tr[x];
}
void merge(int x, int y) {
	int root_x = find(x), root_y = find(y);
	tr[root_y] = root_x;
}
void solve() {
	int n, m;
	cin >> n >> m;
	initial(n);
	while (m--) {
		char opt;
		int x, y;
		cin >> opt >> x >> y;
		if (opt == 'E') merge(x, y + n), merge(y, x + n);
		if (opt == 'F') merge(x, y);
	}
	int res = 0;
	//在上述代码中，我们始终是把tr前面的即朋友部分作为根节点，所以最后有几棵树就有多少个圈子
	for (int i = 1; i <= n; i++) res += tr[i] == i ? 1 : 0;
	cout << res << endl;
}
int main() {
	int _ = 1;
	while (_--) solve();
	return 0;
}

logu P1525 关押罪犯

原题链接
假设发生最大的事情x，则大于x的两个人一定在两个不同的监狱中。所以，我们从最大的影响开始，出现的第一矛盾点就是必须发生的最大影响，有代码如下：

#include <algorithm>
#include <iostream>
using namespace std;
const int N = 10e5 + 10;
int tr[N], data[N];
struct DA {
	int x, y, val;
};
void initial(int n) {
	for (int i = 1; i <= 2 * n; i++) tr[i] = i;
}
int find(int x) {
	if (tr[x] == x) return x;
	tr[x] = find(tr[x]);
	return tr[x];
}
void merge(int x, int y) {
	int root_x = find(x), root_y = find(y);
	tr[root_y] = root_x;
}
bool cmp(DA &a, DA &b) {
	return a.val > b.val;
}
void solve() {
	int n, m;
	cin >> n >> m;
	DA *da = new DA[m];
	for (int i = 0; i < m; i++) {
		int x, y, val;
		cin >> x >> y >> val;
		da[i].x = x, da[i].y = y, da[i].val = val;
	}
	sort(da, da + m, cmp);
	initial(n);
	int res = 0;
	for (int i = 0; i < m; i++) {
		int x = da[i].x, y = da[i].y, val = da[i].val;
		if (find(x) == find(y)){
			res = val;
			break;
		}
		else {
			merge(x, y + n), merge(y, x + n);
		}
	}
	cout << res << endl;
}
int main() {
	int _ = 1;
	while (_--) solve();
	return 0;
}

带权并查集

未完待续。