树状数组(Binary Index Tree)
一、问题引入
Logu P3374
模版题--树状数组。
初始化一个数组,接下来进行若干次以下操作:
- 单点修改:将某个元素的值进行修改
- 区间访问:返回该区间的总和
问题分析
如果通过简单索引操作,“1”的时间复杂度为 O(1),“2”的时间复杂度为O(n),其中如果使用一个dp表的方式来存储前n项之和,那么“2”的时间复杂度为O(1),但是一旦要进行修改操作则变成\(O(n^2)\),显然,我们需要一种更有效的数据结构来维护我们的列表
二、树状数组
我们是否可以这样想:如果我们构造一个数组,其第i个元素包含前i项之和,但是这样不适合经常修改的元素列表,我是否可以将列表划分成n份,用这n段的和来构造这个函数?
显然,如果我们进行修改操作,对其中那个数组就还是回归到了原问题上面.因此,树状数组应运而生
Lowbit操作
假设x = \((10100100)_2\),则定义:
即lowbit(x)表示x的二进制下从左往右数第一个1及其后面所有0(个人理解,其实就是按2的次幂为间隔划分原序列数组,只不过正好有规律,不然以其他数的次幂划分也行)
由于有符号数字在计算机中以补码的形式存在,则\(-x = (01011011)_2 + 1_2 = (01011100)_2\),发现只有lowbit(x)相同,其余都不同,于是有:
树状数组的构建
如图:
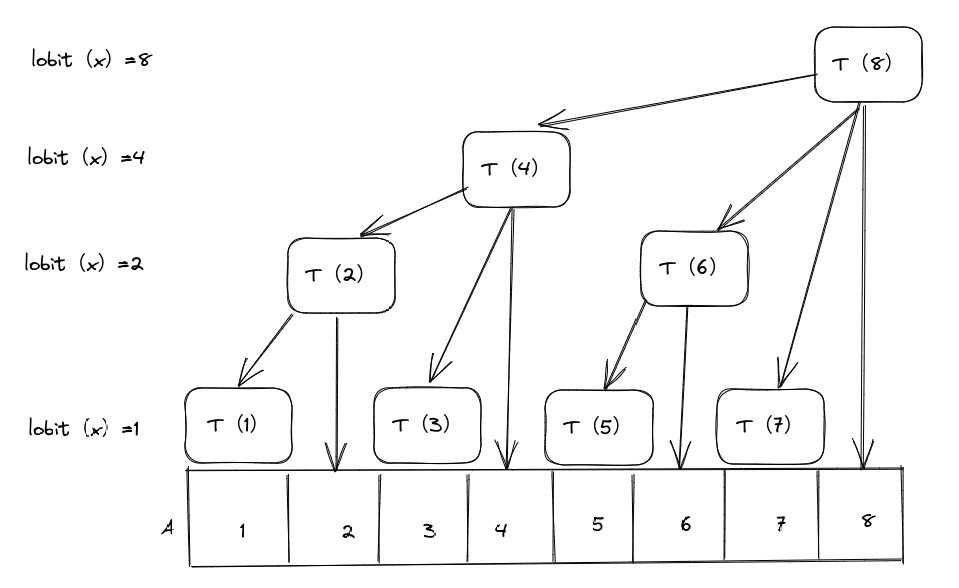
在原数组上面构建树状数组T[],观察到有如下规律:
- 对某一层数i,有lobit(x) = i,并且其子节点也为lowbit(x)
- 数最高为\(log_2 n +1\)
- 对于某一个子节点T[x],其父节点为:T[x+lowbit(x)]
- 前n个元素之和为T[n]+T[n-lowbit(n)]+T[n-lowbit(n)-lowbit(n-lowbit(n))]+....
经过如上规律,我们可以写出代码:
单点修改
void add(int x, int k) {
for (; x <= n; x += x & -x) T[x] += k;
}
区间访问
int ask(int x) {
int res = 0;
for (; x; x -= x & -x) res += T[x];
return res;
}
三、其他操作
区间修改、单点查询
我们构建一个树状数组,用来存放原数组的差分,此时该树状数组的前n项和为A[n],当我们需要对x-y之间加上或减去相同值是,在树状数组的两个元素之间只有第x个和第y+1个的值发生改变,于是只需添加:
add(x, k);
add(y+1, -k);
要进行单点查询只需求和即ask即可
区间修改、区间查询
我们知道在构建差分数组的情况下,前n项和为:
如图:
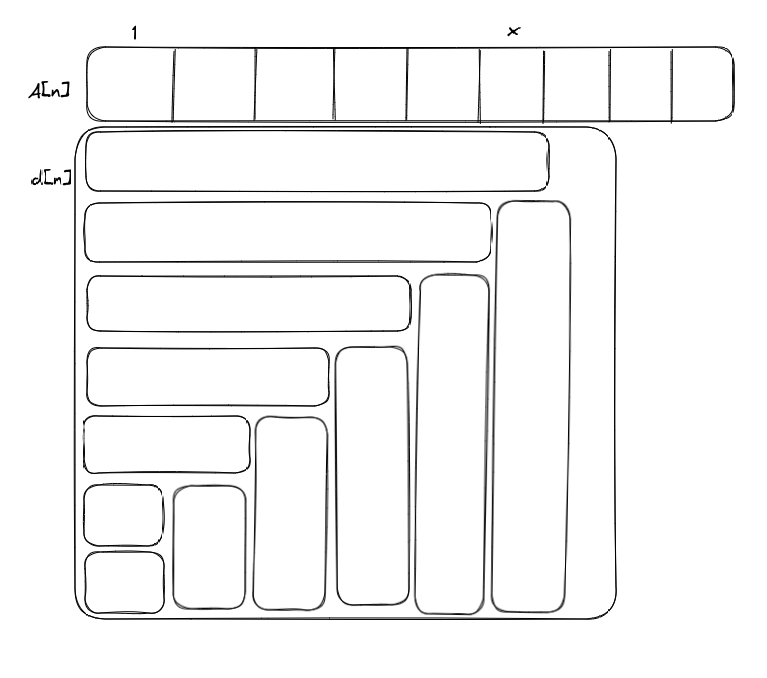
有:
至于要在上面情况的基础上构建一个新的树状数组用来存储id[i]即可完成
于是有:
//区间修改
//d[i]操作不变,对新构建的id[i]:
add(x,x*k);
add(y+1,-(y+1)*k);
//区间访问:
res = (1+x)ask(x) - ask_new(x)
应用举例
1. 逆序数
题干引入
洛谷 P1908
LeedCode LCR 170
逆序数
(和线代中定义一致)在一个数字序列中,后面比前面小的数字个数之和
如 8 4 5 9 1 2 3 3 的逆序数为:6 +4 + 4+ 4+ 0+ 0+ 0 +0 = 18
使用一种办法求出逆序数
树状数组解法
根据上面序列中的数组出现次数,可以构建如下桶:
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| num | 1 | 1 | 2 | 1 | 1 | 0 | 0 | 1 | 1 |
我们根据上面的表构建树状数组
当我们从原列表的后面向前面遍历,储水式num都为0,对元素 \(a_{i}\),将其在表中的num+1,我们发现其逆序数就等于表前面小于 $a_i $ 元素的num之和。(因为是从后面遍历,如果比该元素小的且在后面的已经遍历过
因此:只需要每次加上 \(a_i\)前面之和即可
离散化
我们发现,如果序列为 1 2 100000000000000000000000 ... 就会造成构建树状数组的时候非常大,中间大量空间被浪费,因此我们先进行离散化
代码:
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 5 * 10e5 + 10;
int t[N], record[N], temp[N];
int n;
void Madd(int x, int k) {
for (; x <= n; x += x & -x) t[x] += k;
}
int Mask(int x) {
int res = 0;
for (; x; x -= x & -x) res += t[x];
return res;
}
//离散化时使用sort函数用来比较的函数
bool cmp(int a, int b) {
return a < b;
}
int main() {
int _ = 1;
while (_--) solve();
return 0;
}
solve()函数具体步骤:
void solve() {
//接受输入
cin >> n;
for (int i = 0; i < n; i++) cin >> record[i], temp[i] = record[i];
//离散化
sort(temp, temp + n, cmp);
//lower_bound返回record[i]在temp数组中对应位置的迭代器,减去temp再加1即可获得record[i]在原数组中排序好之后的位置
for (int i = 0; i < n; i++) record[i] = lower_bound(temp, temp + n, record[i]) - temp + 1;
long long res = 0;
for (int i = n; i > 0; i--) {
Madd(record[i - 1], 1);
res += Mask(record[i - 1] - 1);
}
cout << res << endl;
}



