库伦定律
设真空中两点电荷\(q_{1}, q_{2}\),距离为\(r\),他们之间的库仑力为:
\[\vec{F} = \frac{kq_{1}q_{2}}{r^{2}}\vec{r} = \frac{q_{1}q_{2}}{4\pi\varepsilon_{0}r^{3}}\vec{r}
\]
其中 \(k=8.986\times10^{9} N\cdot m^{2}/C^{2}\)
电场
\[\vec{E} = \frac{\vec{F}}{q} = \frac{q}{4\pi \varepsilon_{0}r^{3}}\vec{r}
\]
高斯定理
对于一个高斯面,有如下关系
\[\Phi = \iint_{D} \vec{E}d\vec{S} = \frac{\sum q_{i}}{\varepsilon_{0}}
\]
其中\(q_{i}\)是高斯面内部的电荷
ps. 高斯定理用来求解电场强度时,要求在该高斯面上\(\vec{E}\cdot\vec{S}的夹角有某种规律\),不然仍然无法使用高斯定理来求解电场分布
几种特殊模型的电场分布
均匀带电球体的电场分布
如图
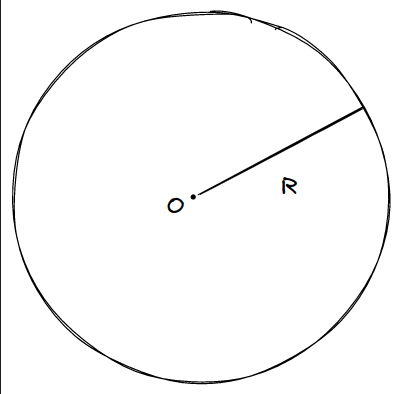
- 当\(r<R\)时,以O为球心做一个高斯面,此时有:
\[\iint\vec{E}\cdot d\vec{S} = E4\pi r^{2} = \frac{4\pi r^{3} \rho}{3\epsilon_{0}}
\]
从而
\[E = \frac{\rho r}{3\epsilon_{0}}
\]
- 同理,当\(r>R\)时,有:
\[E = \frac{R^{3}\rho}{3\epsilon_{0}r^{2}}
\]
画出图像有:
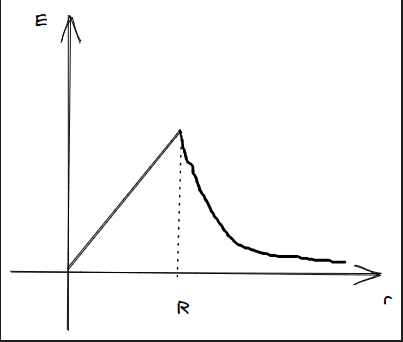
均匀带电球壳
- 当\(r<R\)时,有:
\[E = 0
\]
- 当\(r>R\)时,有:
\[E = \frac{\rho R^{2}}{\epsilon_{0}r^{2}}
\]
同理,画出图像有:
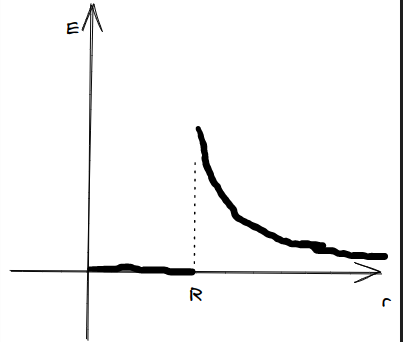
均匀带电圆面
如图
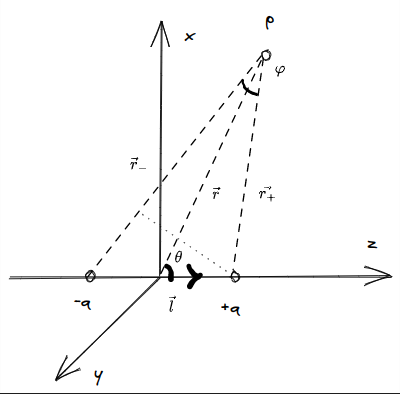
由于对称性可知水平方向电场强度为0,对竖直方向,有:
\[E = \int_{0}^{2\pi}\frac{\sigma R \cos\theta}{4\pi \epsilon_{0}(x^{2}+R^{2})}d\varphi =\int_{0}^{2\pi}\frac{\sigma R x}{4\pi \epsilon_{0}(x^{2}+R^{2})^{\frac{3}{2}}}d\varphi
\]
假设当\(R>>x\),即平面为无穷平面时,产生的场强为:
\[E = \frac{\sigma}{2\epsilon_{0}}
\]
电势
对于一个点电荷,在距离其r处电势为:
\[u = \frac{q}{4\pi\epsilon_{0}r}
\]
对于一个均匀带电球类体,距离其圆心为r处的电势:
\[u = \frac{1}{q} \int_{r}^{\infty}\vec{E}d\vec{r}
\]
利用上面的场强公式,切在均匀的情况下电场方向和半径方向一致,故可很容易得到电势公式。
电偶极子的电势差
如图
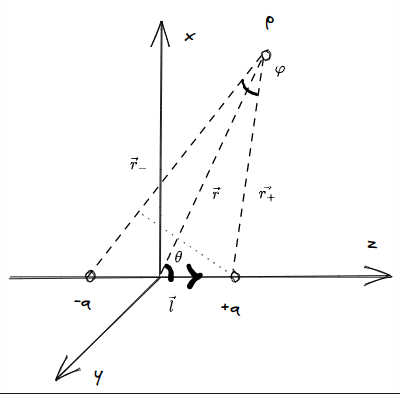
在p点,有电势
\[u = \frac{q}{4\pi\epsilon_{0}}\left(\frac{1}{r_{+}}- \frac{1}{r_{-}}\right)= \frac{q}{4\pi\epsilon_{0}}\cdot \frac{r_{-}-r_{+}}{r_{-}r_{+}}
\]
当\(r>>l\)时,有 \(\varphi\to0\) ,此时\(r_{-}-r_{+}\approx l\cos\theta\),此时有:
\[u = \frac{ql\cos\theta}{4\pi\epsilon_{0}r^{2}}
\]
又有:
\[\vec{p} = q\vec{l} \qquad \cos\theta = \frac{z}{r} = \frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}
\]
所以有电偶极子在无穷远点处的电势分布情况为:
\[u = \frac{pz}{4\pi\epsilon_{0}(x^{2}+y^{2}+z^{2})^{\frac{3}{2}}}
\]
电势求法小结
-
根据电场分布来求电势分布
如对于均匀带点介质,可以通过高斯定理很容易求出其电场分布,再利用某点的电势等于单位正电荷移动到无穷远点(零电势点)电场力做功。
-
根据电荷分布来求电势
已经推导处出点电荷的电势分布规律,利用某点的电势等于所有电荷在该点电势的代数和来求出电势。如不均匀的圆环在中心轴线处的电势与带等量电荷的均匀带点圆环在同一位置处电势一致。
电势和电场强度的微分关系
假设在两个等势面\(u和u+du\),有如下关系:
\[-qdu = q\vec{E}d\vec{l} = qEdl\cos\theta
\]
所以有:
\[E_{l} = E\cos\theta = -\frac{du}{dl} = -\frac{\partial{u}}{\partial x}-\frac{\partial{u}}{\partial x}-\frac{\partial{u}}{\partial x} = -grad(u)
\]
该公式表述含义为:相邻等势面中沿某一方向的电场强度等于该方向电势分布的负梯度
使用举例:我们之前讨论的电偶极子在空间中电势的分布,因此可以利用其电势分布的负梯度来获得每个方向电场强度的大小。
静电场的环路定理
在静电场中,沿任意闭合路径的电场力做功积分为0
- 说明了静电场是一个无旋场
- 说明了静电场中同一条电场线不能首尾相连
- 不能说明静电场是不是有源或者无源场(虽然静电场是有源场)
- 环路定理成立是该场为静电场的必要不充分条件,可以用该条件判断某电场不是静电场








