割点割边桥

当我们学完图的连通性（tarjan）之后就可以学习一下内容了

割点

在无向图中，当我们删除这个点时，图的连通性改变了

比如一张图中本来只有一个连通分量，删除某个点后，这张图的连通分量变成了两个，那么这个点就是割点

割边（桥）

在无向图中，当我们删除这条边时，图的连通性改变了

比如一张图中本来只有一个连通分量，删除某条边后，这张图的连通分量变成了两个，那么这条边就是割边（桥）

割点的判断与证明

其实两个判断就可以判定它是否是割点

（1）low[v]>=dfn[u]&&u!=root
（2）u==root&&son>=2

注：

\(root\)是当前跑\(tarjan\)的节点并非整张图的根节点（可以在跑\(tarjan\)的时候当做参数传入函数，并且每次递归式不变）

\(son\)是相对于当前节点的儿子个数（可以在每次递归的函数中定义这个变量，这样就可以保证每个节点的儿子数被保留并且其它节点的儿子不会影响当前节点的儿子）

\(u\)是当前这个节点

证明（1）

我们依旧用\((x,y)\)来表示\((dfn[i],low[i])\)

图中点为假设，\(u\)为当前节点（非root）

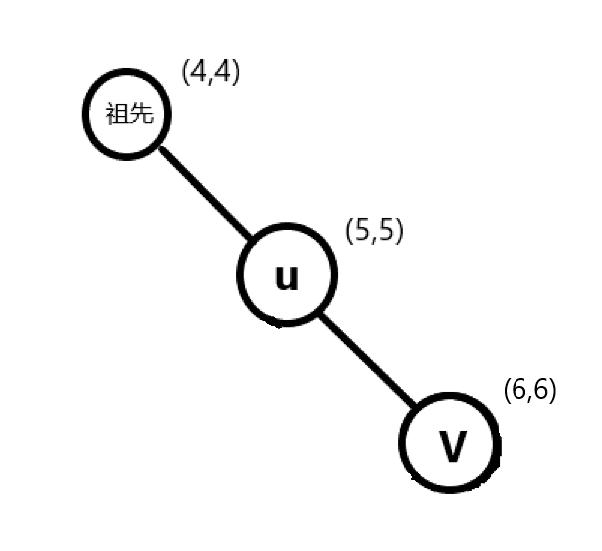
首先是满足第一条中的\(u!=root\)，然后\(low[v]\)与\(dfn[u]\)分三种情况讨论

① \(low[v]>dfn[u]\)

其实就是\(v\)点无法被更早的点更新

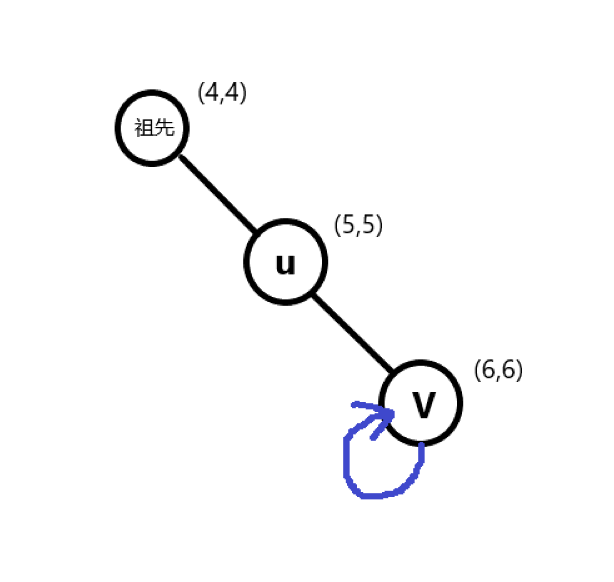
很显然当我们割掉\(u\)点后图的连通性就改变了

因为\(v\)点没有能力回去与\(u\)的祖先们相连，只能乖乖与它们断开联系

②\(low[v]==dfn[u]\)

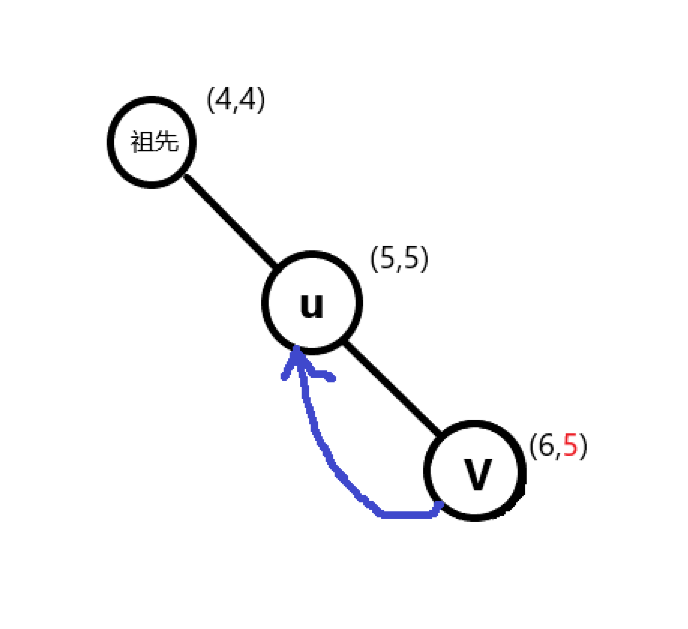
这时候\(v\)可以了，它回到了比自己更早的\(u\)点，但残酷的现实告诉它，割掉\(u\)点后你还是跟\(u\)的祖先们失去了联系

③\(low[v]<dfn[u]\)

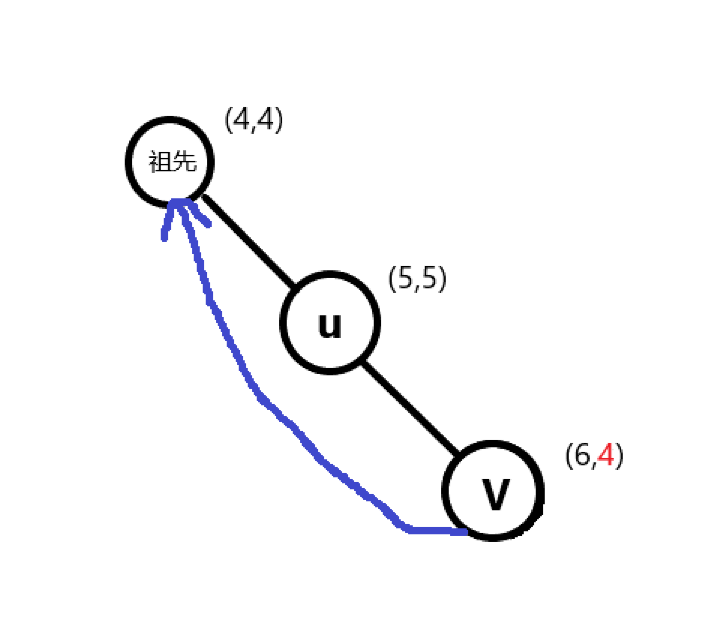
这次\(v\)很好啊，它回到了\(u\)的祖先，可怜的\(u\)被割掉后看这\(v\)和自己的祖先亲热，心里实在不舒服，但又没办法，只能眼睁睁的看着它们在一起

由以上三点可以总结出只有当\(low[v]>=dfn[u]\)时\(v\)点才会与\(u\)的祖先失联(恋),此时图的连通性改变，这个\(u\)就是个割点

证明（2）

还有一种就是\(u\)点是\(root\)

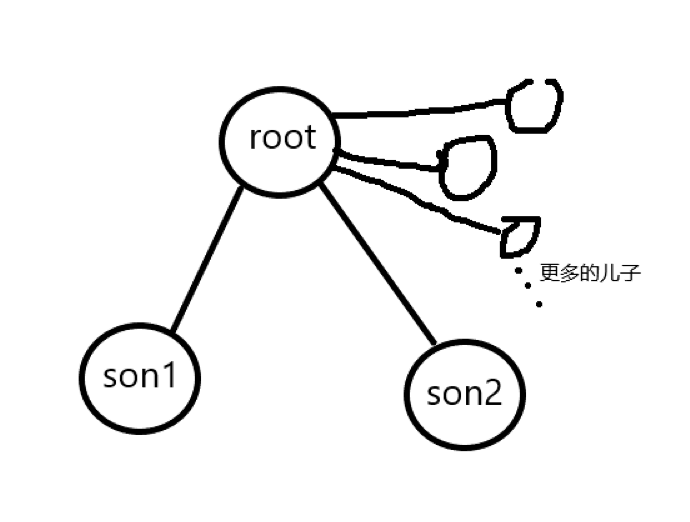
这个应该是很显然的了，当我们把\(root\)割掉之后各个儿子之间的联系就没了，图的连通性就改变了

这里需要注意的是

这个\(root\)与\(san\)的关系是建立在深度搜索树上的，也就是你访问的各节点的顺序,并非原图的\(root\)与\(son\)的关系

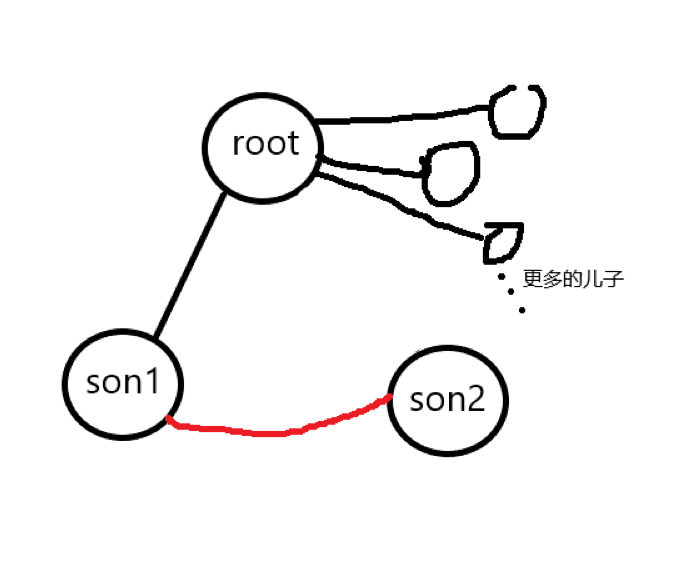
还有一种特殊情况是\(son1\)和\(son2\)之间也有连边（忽略"更多的儿子"）

你可能会觉得割掉\(root\)后也不影响连通性啊

但是回看上面的注意：\(root\)与\(son\)的关系是建立在深度搜索树上的

也就是说在图中两儿子的确有连边，但是在访问过程中\(son2\)是有\(son1\)访问的而并非\(root\)，所以\(root\)与\(son2\)之间不能有连边，即root只有一个儿子，两个判断均不满足，所以不是割点，割掉不影响连通性

桥的判断与证明

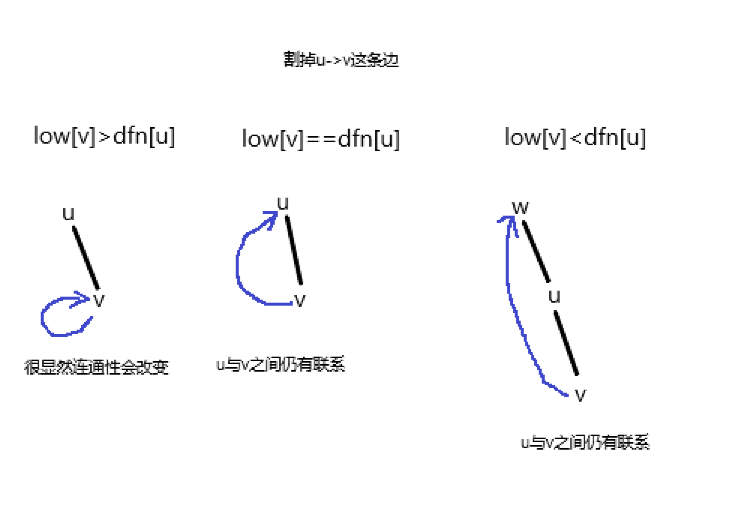
若\(u->v\)是桥则满足

low[v]>dfn[u]

其实与割点的证明相似，所以我就只放一张图啦\(o(*￣︶￣*)o\)

求割点及割边代码

#include<bits/stdc++.h>
using namespace std;
const int M=1000001;
int read() {
    int x(0);bool f(0);char c(getchar());
    while(c<'0'||c>'9') {f^=c=='-';c=getchar();}
    while(c>='0'&&c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
    return f?(~x)+1:x;
}
int dfn[M],low[M],s[M],tot;
stack<int>g;
struct op {
    int to,nxt; 
}e[M];
int head[M],num;
void add(int frm,int to) {
    e[++num].nxt=head[frm];
    e[num].to=to;
    head[frm]=num;
}
set<int>k;//方便储存有序的割点
set<pair<int,int> >kk;//方便储存有序的割边
int sum=0;
void tarjan(int u,int root) {//传参时把root传上
    dfn[u]=low[u]=++tot;//tarjan
    int son=0;//记录当前节点儿子的个数
    for(int i=head[u];i;i=e[i].nxt) {//tarjan
        int v=e[i].to;
        if(dfn[v]==0) {//tarjan
            tarjan(v,root);//tarjan
            low[u]=min(low[u],low[v]);//tarjan
            if(low[v]>=dfn[u]&&u!=root) {//割点（1）
                k.insert(u);//把割点存起来
            }
            if(low[v]>dfn[u]) {//割边
            	kk.insert(make_pair(u,v));//把割边储存起来，可以改为结构体
            }
            if(u==root) son++;//记录儿子的个数
        }
        else low[u]=min(low[u],dfn[v]);//tarjan
    }
    if(u==root&&son>=2) k.insert(u);//割点（2），把割点存起来
}
int main() {
    int n=read(),m=read();
    for(int i=1;i<=m;++i) {
        int x=read(),y=read();
        add(x,y);
        add(y,x);
    } 
    for(int i=1;i<=n;++i) if(!dfn[i])tarjan(i,i);//tarjan
    ......
return 0;
}