tarjan算法求强连通分量
前置知识
强连通分量
有向图强 连通分量 :在 有向图 G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点 强连通,如果有向图G的每两个顶点都强连通,称G是一个 强连通图 。有向图的极大强连通子图 ,称为强连通分量。
——————baidu
存图
可以用前向星也可以邻接矩阵
正题
可以结合最后的代码理解一下内容
tarjan算法是用来求有向图中的强连通分量的
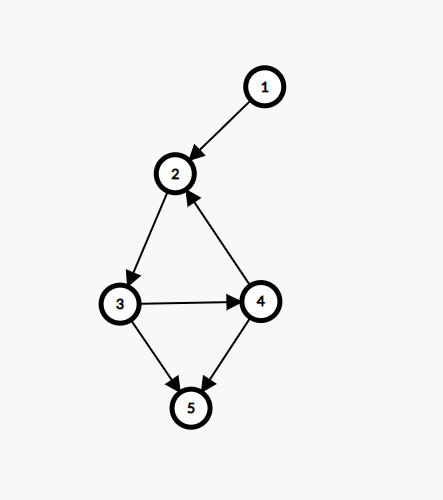
至于一张有向图它会长以上这样
关于算法中会有两个数组\(dfn[i]\)和\(low[i]\)
\(dfn[i]\)姑且可以当作一种标记,标记它是否访问过,它的值是由dfs的顺序产生的,在上面的图中可以当作和标号相同
\(low[i]\)你可以叫它时间戳,很烦,所以就叫它low吧,它在操作过程中是在变化的
我们用\((i,j)\)表示\((dfn[i],low[i])\)
如上图,当我们都访问一遍,仅仅只是初始化,就是下面这张图
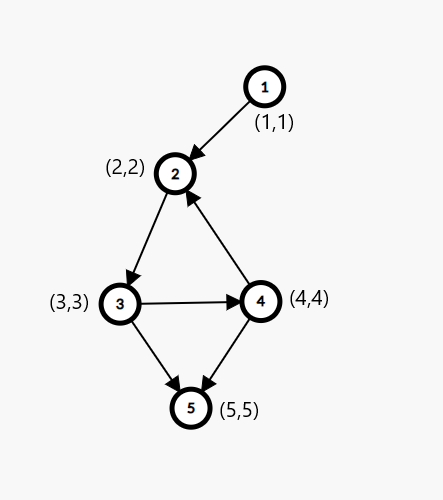
先初始化一个\(tot=0\),每次访问到新的节点是就\(++\),用tot来更新low和dfn
递归访问
我们从1号点开始进行递归
此时 \(tot=1\)并且\(dfn=0\)
先入栈
1号点的low和dfn被更新为1,即表示为\((1,1)\)
继续递归到二号点
此时 \(tot=2\)并且\(dfn=0\)
先入栈
2号点的low和dfn被更新为2,即表示为\((2,2)\)
继续递归到三号点
此时 \(tot=3\)并且\(dfn=0\)
先入栈
3号点的low和dfn被更新为3,即表示为\((3,3)\)
继续递归到四号点
此时 \(tot=4\)并且\(dfn=0\)
先入栈
4号点的low和dfn被更新为4,即表示为\((4,4)\)
随后从四号递归到五号点
此时 \(tot=5\)并且\(dfn=0\)
先入栈
5号点的low和dfn被更新为5,即表示为\((5,5)\)
到这里我们发现五号点没有下一个点了,所以不会继续访问下一个点,即开始对五号点的操作
我们会发现,5号点并没有一条指向其它点的边
所以它会直接进行下一步操作,判断dfn与low是否相等
很显然\(5==5\),所以5这个点是一个单独的强连通分量,再出栈
此时栈中元素有:4,3,2,1
五这个点的递归结束,回到四这个点,对四进行操作
首先5号已经为一个单独的强连通分量了所以不管它
继续遍历,发现2号点的dfn不为0,所以它不会进行递归,而是判断下一步,判断是否在栈中,在就更新,不在就不管了,2号是在栈中的,并且2号的low是远小于4号点的low,所以4号点的low被更新为2,即(4,2)
注:这个判断下一步一般会在这个点有多条边指向其他点,然后这几个其它点中有一个把这个点给访问了,所以就没法递归访问,只能试试在不在栈中能不能更新了
low[4]和dfn[4]不相等
至此四号点遍历结束,回到三号点
三号点之前是对四号点进行访问的4号点,所以会先对4号点进行操作,4号的low是小于3号点的low,所以3号点的low被更新为2,即(3,2)
low[3]与dfn[3]不相等
随后三号点会遍历到五号点并试图递归到五号
发现五号的\(dfn\)不为\(0\),所以它不会进行递归,而是判断下一步,判断它是否在栈中,很显然5号点在之前就已经出栈了,所以什么都不做
注:见上上
low[3]和dfn[3]依然不相等
三号遍历结束,回到二号
2号只能遍历到3号,而2号的low和3号的low大小相同,所以不会被更新,还是(2,2)
二号遍历结束,发现二号的low和dfn相等
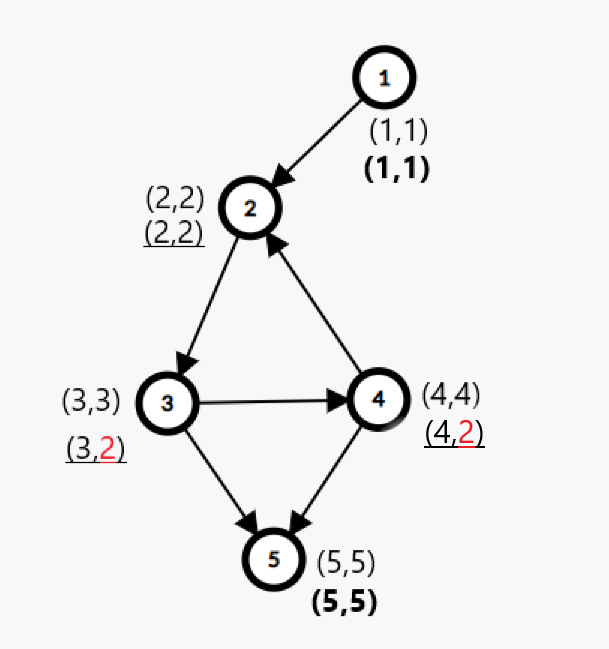
这时图长这样
栈中元素还是:4,3,2,1
我们已经判断到二号点的low和dfn相等且无法被更新了
所以就会有一个以二号点为开头的强连通分量
栈从4弹出到2,
此时4,3,2就是一个强连通分量
再回到一号点
2号点无法更新1号点
low[1]与dfn[1]相等
所以从1号点开始出栈,出到1号,一号作为一个强连通分量
此时栈中空
至此tarjan算法结束
强连通分量有5 4,3,2 1 共三个
最后附上代码以供理解
#include<bits/stdc++.h>
using namespace std;
const int M=1000001;
int read() {
int x(0);bool f(0);char c(getchar());
while(c<'0'||c>'9') {f^=c=='-';c=getchar();}
while(c>='0'&&c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return f?(~x)+1:x;
}
int dfn[M],low[M],head[M],num,s[M],tot,res,ans[M],out;
stack<int>g;
struct op {
int nxt,to,dis;
}e[M];
void add(int frm,int to) {
e[++num].nxt=head[frm];
e[num].to=to;
head[frm]=num;
}
void tarjan(int u) {
low[u]=dfn[u]=++tot;//访问时的更新
g.push(u);//入栈(只要在栈中就说明还没有被列为强连通分量)
s[u]=1;//标记已经在栈中了
for(int i=head[u];i;i=e[i].nxt) {//遍历这个点所有指向其它点的有向边
int v=e[i].to;//其实遍历边就相当于遍历这个点所指向的其它的点
if(dfn[v]==0) {//如果这个点之前没有访问过
tarjan(v);//访问这个点
low[u]=min(low[u],low[v]);//访问完这个点之后的所有点后,回来后对这个点进行更新
}
else if(s[v]) {//这个点访问过了(这个点之前的点把这个点给访问了),并且它还在栈中(就是还没有被列为一个强连通分量)
low[u]=min(low[u],low[v]);//对这个点进行更新
}
}
//这个点所有指向其它点的有向边(所指向的其它的点)遍历完了
//若进行了下面一步,说明找到了一个强连通分量
if(low[u]==dfn[u]) {//判断到这个点的low和dfn是相等的(也就是说这个点是一个强连通分量的起点)
while(g.top()!=u) {//栈中后入的元素是在上面的,并且这个点后面(递归返回的时候是倒着的)的强连通分量已经被找到并弹出来,所以不必担心会有其它点的影响。
//所以我们就一直弹,弹到当前这个点为止,弹出的这些点就是一组强连通分量
int w=g.top();
g.pop();//弹出元素
s[w]=0;//标记它已经不在栈中了
}
//这个点自身也是这个强连通分量中的一个,所以也要弹出标记
g.pop();
s[u]=0;
//因为写stack的话感觉会好理解点,如果你要手写栈,就可以用do{}while;来避免这个点自己出不了栈了
}
}
int main() {
int n=read(),m=read();
for(int i=1;i<=m;++i) {
int u=read(),v=read();
add(u,v);
}
for(int i=1;i<=n;++i) {
if(!dfn[i])tarjan(i);
}
return 0;
}
无注释版本
#include<bits/stdc++.h>
using namespace std;
const int M=1000001;
int read() {
int x(0);bool f(0);char c(getchar());
while(c<'0'||c>'9') {f^=c=='-';c=getchar();}
while(c>='0'&&c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return f?(~x)+1:x;
}
int dfn[M],low[M],head[M],num,s[M],tot,res,ans[M],out;
stack<int>g;
struct op {
int nxt,to,dis;
}e[M];
void add(int frm,int to) {
e[++num].nxt=head[frm];
e[num].to=to;
head[frm]=num;
}
void tarjan(int u) {
low[u]=dfn[u]=++tot;
g.push(u);
s[u]=1;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].to;
if(dfn[v]==0) {
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(s[v]) {
low[u]=min(low[u],low[v]);
}
}
if(low[u]==dfn[u]) {
while(g.top()!=u) {
int w=g.top();
g.pop();
s[w]=0;
}
g.pop();
s[u]=0;
}
}
int main() {
int n=read(),m=read();
for(int i=1;i<=m;++i) {
int u=read(),v=read();
add(u,v);
}
for(int i=1;i<=n;++i) {
if(!dfn[i])tarjan(i);
}
return 0;
}


