Uva_11722 Joining with Friend

题目链接

题意：

　　两个人坐火车， 在某个城市到站的时间段分别为[t1, t2] , [s1, s2]，停在站台的时间均为w。

　　问， 若两人能见面的概率。

 

思路：

　　一道基础的几何概型， p = s(m)/s(n)。

　　令x1 = t1, x2 = t2。

　　令y1 = s1, y2 = s2。

　　这样这四条直线就围成一个矩形，若两人见面， 则应该满足在 y = x ± w 这两条直线之间。

　　即本题求解， y = x ± w 在矩形中所围面积 与矩形面积之比。

　　根据 y = x + b 这条线与矩形的交点不同， 把矩形分成四个区域， 计算面积这里规定以左上角的点为参考点计算。

　　阴影面积即为所求

　　1）

　　

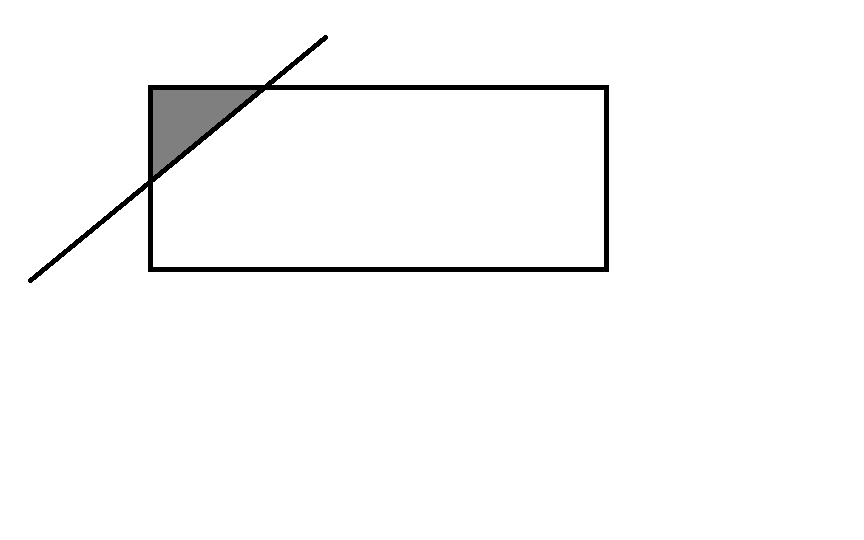
　　2）

　　这种情况将之补成一个三角形， 用大三角形减去小三角形的面积即可。

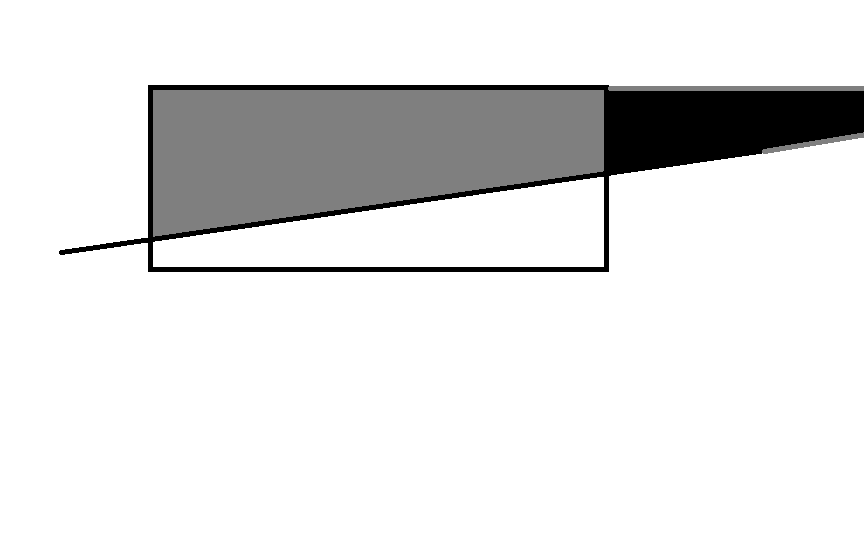
　　3）

　　这种情况， 用矩形面积减去小三角形面积即可。

　　4）

　　这种情况也用补全三角形来求解

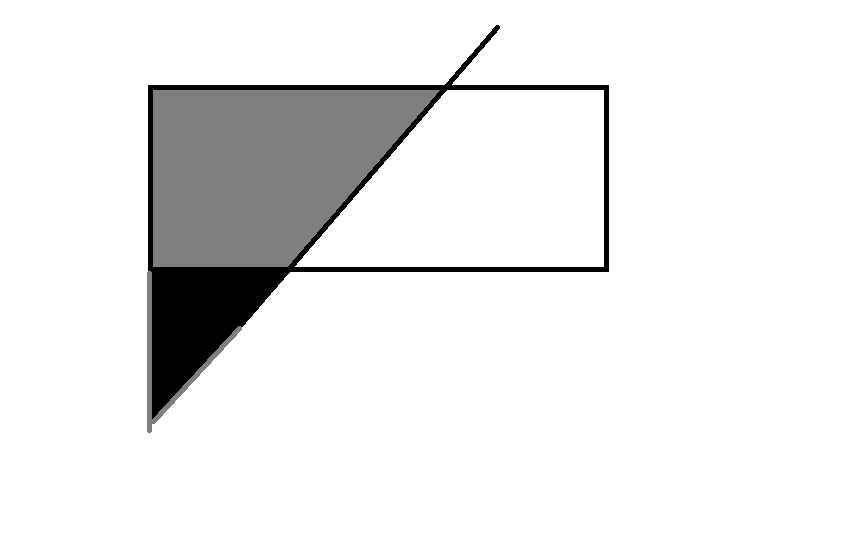
　　other)

　　如果直线相交于左上角， 那么面积为0. 如果在右下角， 那么面积为矩形面积。

　　

 

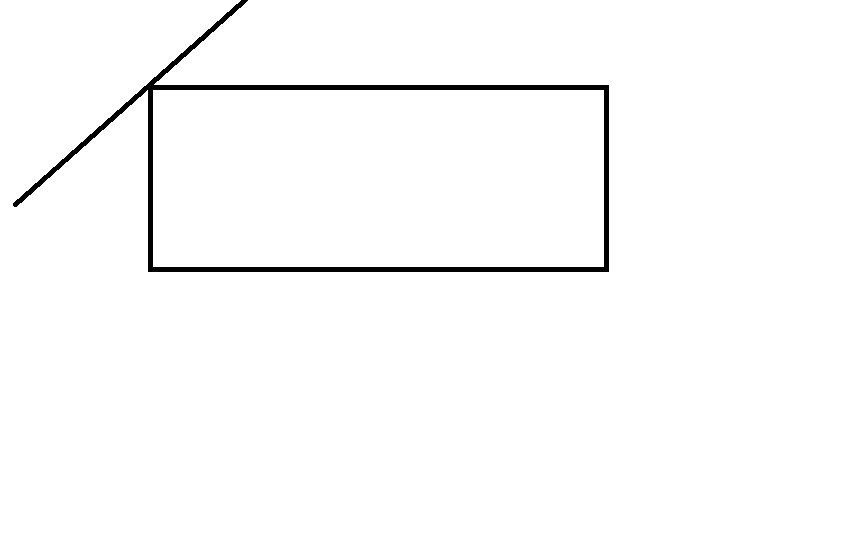
代码如下：

 1 #include <cmath>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cstdlib>
 5 #include <ctime>
 6 #include <climits>
 7 #include <set>
 8 #include <map>
 9 #include <list>
10 #include <queue>
11 #include <string>
12 #include <vector>
13 #include <fstream>
14 #include <iterator>
15 #include <iostream>
16 #include <algorithm>
17 using namespace std;
18 #define LL long long
19 #define MAXN 4
20 #define MOD 1000000007
21 #define eps 1e-6
22 double s[MAXN], t[MAXN], w;
23 double weight, high;
24 double get_area(double b)
25 {
26     double tx = t[2] - b;
27     double dx = t[1] - b;
28     double ly = s[1] + b;
29     double ry = s[2] + b;
30     //printf("tx: %.7lf, dx: %.7lf, ly: %.7lf, ry: %.7lf\n", tx, dx, ly, ry);
31     bool OnTop = (tx <= s[2] && tx >= s[1]);
32     bool OnDown = (dx <= s[2] && dx >= s[1]);
33     bool OnLeft = (ly <= t[2] && ly >= t[1]);
34     bool OnRight = (ry <= t[2] && ry >= t[1]);
35 
36     if(OnTop && OnLeft)
37         return 0.5 * (tx - s[1]) * (t[2] - ly);
38     if(OnLeft && OnRight)
39         return 0.5 * ((t[2] - ly) * (tx - s[1]) - (t[2] - ry) * (tx - s[2]));
40     if(OnDown && OnTop)
41         return 0.5 * ((tx - s[1]) * (t[2] - ly) - (dx - s[1]) * (t[1] - ly));
42     if(OnDown && OnRight)
43         return weight * high - 0.5 * (s[2] - dx) * (ry - t[1]);
44     return ly >= t[2] ? 0 : weight * high;
45 }
46 
47 int main()
48 {
49     int T;
50     int kcase = 0;
51     scanf("%d", &T);
52     while(T --)
53     {
54         scanf("%lf %lf %lf %lf %lf", &t[1], &t[2], &s[1], &s[2], &w);
55         high = t[2] - t[1];
56         weight = s[2] - s[1];
57         double area_top = get_area(w);
58         double area_down = get_area(-1 * w);
59         double ans = high * weight;
60         //printf("%.8lf %.8lf %.8lf\n", area_top, area_down, ans);
61         ans = (area_down - area_top) / ans;
62         printf("Case #%d: %.8lf\n", ++ kcase, ans);
63     }
64     return 0;
65 }
View Code

 

posted @ 2015-07-28 11:42  若羽。  阅读(239)  评论(0)  编辑  收藏  举报