POJ #1328 Radar Installation 区间贪心 数学题(雾
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
Figure A Sample Input of Radar InstallationsInput
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zerosOutput
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0Sample Output
Case 1: 2 Case 2: 1
更多测试样例点我:测试样例
思路
吐槽时刻,这道题要特别注意精度问题,岛屿位置和雷达半径是整数,如果当成 double 型计算会导致 TLE。这个狗血的TLE一度让我怀疑C++ vector 是不是真的比内置数组慢太多了...事实证明 c++ 的 vector 当成定长数组计算的话还是很快的。
回到原题,读完问题后,我们发现从无解情况入手是比较容易的。什么时候会无解呢?即存在一个以岛屿位置为圆心、雷达覆盖半径为半径的圆与 y = 0 联立后都没有解,即 delta < 0 ,化简后可以表示为 yi - d > 0 。
那么什么时候会有解呢?delta >= 0 时会有解,而且方程联立后会得到两个根,雷达必须修在这两个根之间才能保证覆盖到该岛屿。很显然不需要为每个岛屿都修一个雷达站,因为如果两个岛屿在 x 轴上的根的范围是存在交集的话,就可以只修一个雷达站在交集的范围里。
这时候贪心策略就出来了:我们先对 x 轴上的根区间以左根的大小进行一次排序,然后拿第一个根区间和第二个根区间的交集 tmp 去往后比对,如果之后的根区间和它交集为空,那么代表当前修的雷达站覆盖不了之后的岛屿,需要在这个根区间里再修一个雷达站,并把 tmp 替换成这个新的根区间;如果之后的根区间和它有交集,那么把 tmp 替换为当前的交集,代表当前修的雷达站只有在当前的这个区间里,才能覆盖当前岛屿 ... 如此比对,直到最后一个根区间比对完毕。
举个例子,现在有四个岛屿以及建雷达时能被覆盖的根区间分别为 (-8, 2) 、(-7, -1)、(0, 0)、(1, 11) 。抽象成二维平面图如下:
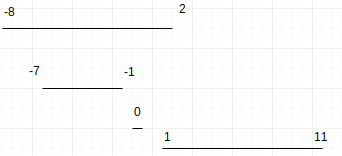
取第一个根区间和第二个根区间的交集为 tmp, tmp 为 [-7, -1] 。它和之后的 [0, 0] 比对后,发现交集为空,那么就需要在 [0, 0] 内多修一个雷达站,并替换 tmp 为新的根区间 [0, 0]。之后发现和 [1, 11] 的交集还是为空,那么在 [1, 11] 内多修一个雷达站,并替换 tmp 为 [1, 11] 。最后得到结果为 3。
在实际敲代码时,可以把 tmp 区间换为一个记录交集右边界的变量。

#include<iostream> #include<algorithm> #include<vector> #include<cstdio> #include<cmath> using namespace std; struct Island { int x; int y; double delta; double left_root; double right_root; }; const int MAX_N = 1000; vector<Island> vec1; //vec1 存储岛屿信息 bool cmp (const Island& a, const Island& b) { return a.left_root < b.left_root; } int main(void) { int case_num = 0; int n; //岛屿数 int d; //雷达覆盖半径 while( cin >> n >> d) { if (n == 0 && d == 0) break; case_num++; vec1.resize(n+1); bool is_all_cover = true; for (int i = 1; i <= n; i++) { cin >> vec1[i].x >> vec1[i].y; vec1[i].delta = d * d - vec1[i].y * vec1[i].y; //将系数4忽略后的delta,便于计算开方 //与y = 0 联立,有解时 if (vec1[i].delta >= 0) { double sqrt_val = sqrt(vec1[i].delta); vec1[i].left_root = vec1[i].x - sqrt_val; vec1[i].right_root = vec1[i].x + sqrt_val; } //存在一个岛屿无法被覆盖,问题无法解决 else { is_all_cover = false; } } //无解情况, 1.雷达覆盖半径是负数 2.存在岛屿无法被覆盖 if (d < 0) { cout << "Case " << case_num << ": " << -1 << endl; continue; } if (!is_all_cover){ cout << "Case " << case_num << ": " << -1 << endl; continue; } //有解情况,解决雷达站重复覆盖问题 std::sort(vec1.begin() + 1, vec1.end(), cmp); int radar_num = 1; //雷达站数目 double tmp = vec1[1].right_root; for (int i = 2; i <= n; i++) { if (vec1[i].left_root > tmp) { radar_num++; tmp = vec1[i].right_root; } else if (vec1[i].right_root < tmp) { tmp = vec1[i].right_root; } } cout << "Case " << case_num << ": " << radar_num << endl; vec1.clear(); } vec1.clear(); vector<Island>().swap(vec1); return 0; }



