LeetCode #5 Longest Palindrome 最长回文串 DP

Description

---

 

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

 

Sample

Input: "babad"

Output: "bab"

Note: "aba" is also a valid answer.

Input: "cbbd"

Output: "bb"

 

 

思路

---

 

　　回文串是正着读、反着读都一样的串，比如 "a"、"level"、"noon"。

　　解本道题最无脑的办法肯定是 O(n^3) ，这里不讨论了。

　　我想到了一个 O(n^2) 的办法，由于回文串都是对称的，那么它的中点就十分关键，我们维护一个指针 i 指向回文串的中点，维护一个指针 j 确定回文串的长度，判断序列 S[ i-j .. i ] 与序列 S[ i .. i+j ] 的逆序列S' 是否相同，如果相同，让 j++。

　　举个例子，如 abcba ，当 i = 2 (S[2] = c) 时，j 赋值为 1，使得 s[ i-1..i ] 与 s[ i..i+1 ] 的逆序列分别为 [bc]、[bc] ，两者是相同的，那么就让 j++ 以表示回文串的长度增加，之后再比较 S[i-2..i] 与 s[i..i+2] 的逆序列是否相同...

　　还需要注意回文串的长度分奇偶，比如 "bb"、"bab" ，敲代码的时候也要分别对两种情况进行修改。

 

　　我用 map 去优化这道题存储回文串的运行时间，红黑树实现的map 插入效率为 O(lgn) ，但是算法时间的上界主要受指针 i j 的影响，，所以算法的时间复杂度为 O(n^2 ) ，这儿我想玩玩 map 的比较函数，所以时间会久一点。实际上，用两个变量存储最大回文串的长度与最长回文串就好了。　　

#include<iostream>
#include<algorithm>
#include<map>
using namespace std;
class Solution {
public:
    string longestPalindrome(string s) {        
        int len = 0, maxlen = 0; 
        std::map<int, string, greater<int> > m; //use greater<> sort key instead of default less<>
        string substr = "";
        for (int i = 0; i < s.size(); ++i) {
            findPal(s, i-1, i+1, len, substr); // Palindrome is adjacent
            if (maxlen < len) {
                maxlen = len;
                m[len] = substr;
            }
            findPal(s, i, i+1, len, substr); // Palindrome is not adjacent
            if (maxlen < len) {
                maxlen = len;
                m[len] = substr;
            }
        }
        substr = m.begin()->second; //the first value means longestPalindrome
        return substr; 
    }
private:
    void findPal(const string& s, int left, int right, int& len, string& substring) {
        while (left >= 0 && right <= s.size()-1 && s[left] == s[right]) {
            left--;
            right++;
        }
        len = right -left -1; //subtract extra two lengths
        if (len < 1)
            return; //length of Palindrome must >= 1
        else 
            substring = s.substr(left+1, len);
    }
};

 

　　其实还有一种办法可以更快，那就是采用 区间DP 的 manacher 算法。但是我没悟到，之后理解了会再更新这篇博客。

　　想了很久，只想到了一种 O(n^2) 的区间DP算法(哭 。

　　设回文串的左右下标分别是 i、j ，假设状态 dp[i][j] 表示字符串[i..j] 是否为回文串，显然原问题满足最优子结构的特性且无后效性，那么确定了它的两个边界条件 i == j 、j-i == 1 的情况后，就可以很容易地写出递推式，也就是状态转移方程为：

　　

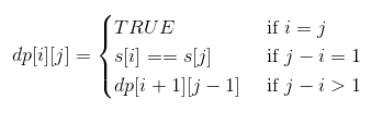
　　知道状态转移方程后，问题就变得简单啦。

#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;

class Solution {
public:
    string longestPalindrome(string s) {
        const int SIZE = s.size();
        bool dp[SIZE][SIZE];
        memset(dp, false, sizeof(dp));
        int max_length = 1;
        int substring_left_index = 0;
        for (int j = 0; j < SIZE; ++j) {
            for (int i = 0; i <= j; ++i) {
                //边界条件
                if (i == j) {
                    dp[i][j] = true;
                }
                //边界条件
                else if (j - i == 1) {
                    dp[i][j] = (s[i] == s[j]);                
                }
                else if (j - i > 1) {
                    dp[i][j] = (s[i] == s[j]) && (dp[i+1][j-1]);
                }
                //record the left index of substr and the length of Pal
                if (dp[i][j] && j-i+1 > max_length ) {
                    max_length = j-i+1;                
                    substring_left_index = i;
                }
            }
        }
        return s.substr(substring_left_index, max_length);
    }
};

int main (void) {
    Solution input;
    string s;
    cin >> s;
    cout << "the longest Palindrome is:" << input.longestPalindrome(s) << endl;
}