《算法导论》 第二章 练习题 Exercise

2.2-1

---

 

Θ(n^3)

 

2.2-2

---

　　

for j = 1 to A.length - 1　　　　
    min = j　　　　　　　　　　　　
//  The minimum value of sequence A [j..A.length-1] is added to the end of sequence A [1..j-1]
    i = j + 1　　　　　　　　 　　
    while i < A.length　　　　　 
        if A[i] < A[min]           
        min = i
    if A[j] != A[min]
        swap A[j] and A[min]    

　　

　　该算法维持的循环不变式：

　　　　I）初始化：循环第一次迭代前，j = 1,子序列 A[1..j-1] 为空。这个序列包含了 j-1 -1 +1 =0 个序列 A[j..A.length-1]中最小的元素。

　　　　II）保持：该算法从序列 A[j..A.length] 中选取一个最小值 A[min] 加入到序列 A[1..j-1] 的末尾，所以在每一次 swap 操作后，子序列 A[1..j] 将包含 j 个元素，且序列 A 的第 j 小的值位于 A[1..j] 第 j 位。随后 j++，为下次迭代重新建立起了循环不变式。

　　　　III）终止：循环结束时 j = A.length，此时在子序列 A[1..j-1] 中有 j-1 = A.length-1 个最小值且第 A.length-1 小的值位于第 A.length-1 位，而对于 A[1..A.length] 而言，剩下一个A[A.length]，而这个第 A.length 小的值刚好位于第 A.length 位。故无需对第 A.length 位运行该算法，因为当循环结束时第 A.length 位自然就排序好了。

　　因为选择排序是对 A[j..A.length] 进行选取最小值的操作，所以对于最好和最坏的情况，运行时间是一样的。

　　由于增长量级最受 while i < A.length 的影响，而这一句的执行次数是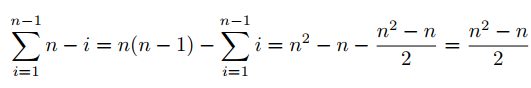 　

　　所以运行时间是 Θ(n^2)

　　　　

2.2-3

---

 

　　平均情况的运行时间的求法：  ，其中 i 是问题规模为 n 的实例， P(i) 是实例 i 的概率，而T(i) 是实例 i 的运行时间。

　　

　　假设序列中的每一个元素都有固定 p 的概率是我们需要查找的元素v。一个序列有 k 个元素，若前 k-1 个元素都不是我们想要的元素，则第 k 个元素是我们想要的元素。这意味着当步数为 k 且它是我们想要的元素的概率是  

　　但也有可能出现所有元素都不是我们想要的元素，它的概率是  

　　通过将步数乘以它对应情况发生的概率，得到期望值关于步数的函数：

　　最坏情况很明显是遍历序列，需要查找 A.length 步，运行时间是 Θ(A.length)

　　接下来计算平均情况，我们先把上面的期望函数化简，化简过程利用了双求和、等差求和与等比求和：

　　

 

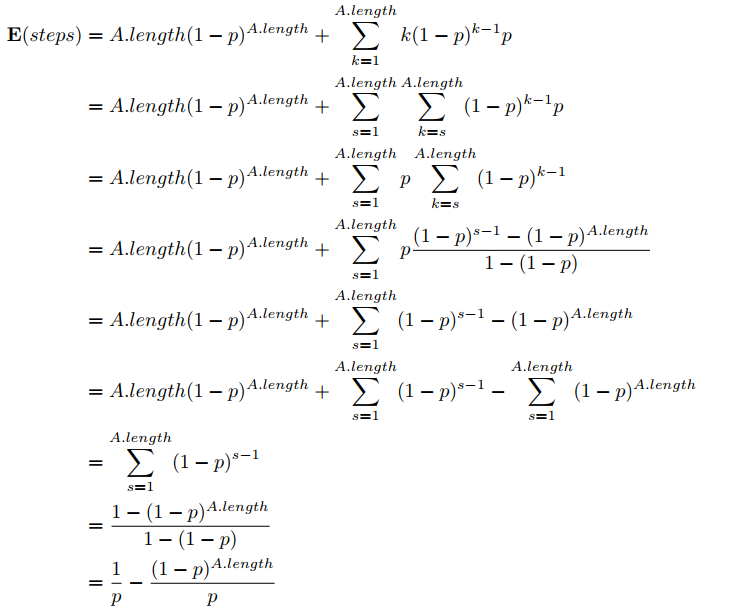
　　因为 > 0，所以 E(steps) <  ，又因为 A.Length ≥ 1，所以

　　因此，对于一个给定上下界的序列，它平均情况的运行时间的增长量级与 p 和 A.length 有关，因为我们在一开始就设了 p 是固定值即 p = Θ(1)，所以现在只考虑序列长度对运行时间的影响，有 T(n) = Θ(A.length)

 

　　当然求平均时间还有另一种的办法，假设这个序列中一定存在你想要的元素，且每一个位置的元素是该元素的概率都是等可能性的，在这种情况下，最坏情况的查找次数与运行时间是不变的，而平均情况的查找次数是   步，运行时间即是 Θ(A.length)

 

2.2-4

---

　　

　　算法刚开始时候先检测数据，如果数据满足特殊条件则直接输出相对应结果，比如一个排序算法，如果输入的数据是顺序的，那么不用再排序而是直接输出即可。

 

2.3-1

---

　　

mergeSort (A, p , r)
    if p < r
        q = ⌊p+r/2⌋ //向下取整
        mergeSort (A, p, q )
        mergeSort (A, q+1, r)
        merge (A, p, q, r)

　　归并排序遵循分治法，在每层递归都有三个步骤：

　　I）分解：将数组A分解成2个子问题，每个问题的规模是原问题的一半，即 A1 = <3, 41, 52, 26>，A2 = <38, 58, 9, 49>

　　II）解决： 使用归并排序对两个子问题进行递归地排序，当待排序的长度为1时，递归“回升”，不做任何操作，因为此时长度为1的序列都是有序的。

　　III）合并：合并两个已经排好序的子序列。

　　base case ：p == r 时序列仅有一个元素，可看作已经是排序好的了，终止递归

　　操作流程图如下：

　　

 

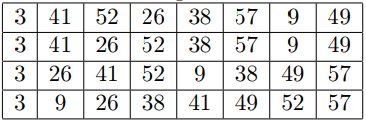
2.3-2

---

　

merge (A, p, q, r)
    n1 = q - p + 1
    n2 = r - q
    let L[1..n1], R[1..n2] be new arrays
    for i = 1 to n1
        L[i] = A[p+i-1]
     for j = 1 to n2
        R[j] = A[q+i]
    i = 1
    j = 1
    for k = p to r
        if i <= n1 and j <= n2
            if L[i] < R[j]
                A[k] = L[i]
                i = i + 1
            else
                A[k] = R[j]
                j = j + 1
        else if i > n1
                A[k] = R[j]
                j = j +1
        else if j > n2
                A[k] = R[i]
                i = i + 1

 

2.3-3

---

　　

　　由题意，设 n = 2^k 。当 k = 1 时，n = 2，T(2) = 2 _lg2 = 2，T(n) = n _lgn 成立。

　　假设当 k 时成立，即 

 

　　当 k+1 时， 有如下推导：

　　

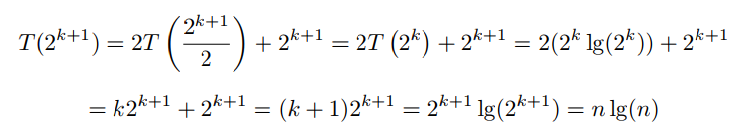
　　所以对n = 2^k，k是任意自然数，该递归式的解都是 　T(n) = n _lgn 　

 

2.3-4

---

　　

　　递归版本的插入排序如下：

insertionSort (A, p, r)
    //base case
    if p == r
        return NIL
    //recursive case
    if p < r
        q = r - 1 
        insertionSort (A, p, q)
        
    //let A[1..i] be sorted
    key = A[r]
    i = q
    while i > 0 and A[i] > key
        A[i+1] = A[i]
        i = i - 1
    A[i+1] = key
    return A

　　

　　最坏运行情况是全部元素都是按逆序排序，需要移动 n-1 次，此时插入步骤所耗的时间将是 Ι(n-1) = Θ(n)

　　

 

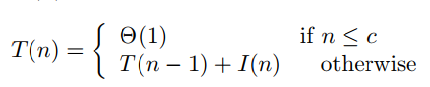
2.3-5

---

 

二分查找迭代版本　　

binarySearch(A, q, r, v)
    while q <= r
        mid = ⌊q+r⌋ / 2
        if A[mid] == v
            reutrn mid
        if A[mid] < v
            q = mid + 1
        else
            r = mid - 1
    return NIL

 

二分查找递归版本

binarySearch (A, p, r, v)
    if p > r
        return NIL
    mid = ⌊p + r⌋ / 2
　　　　
    if A[mid] == v 
        return mid

    //recursive case
    if A[mid] < v
        return binarySearch (A, mid+1, r, v)
    if A[mid] > v
        return binarySearch (A, q, mid-1, v)

 

　　由于二分查找的递归树树高为 _lgn，而每次查找的时间是 Θ(1)，所以它的最坏情况运行时间的递归式是，时间总代价为 c _lgn ∈ Θ(_lgn) 

 

2.3-6

---

 

　　不行。虽然我们可以在插入算法的基础上（插入算法令 A[1..i-1] 保持有序）利用二分查找去优化查询关键字的效率，优化的算法如下

biInsertionSort (A)
    for i = 2 to A.length
        key = A[i]
        low = 1
        high = i - 1
        // find a smaller value than A[i] of sorted sequence A[1..i-1]
        while (low <= high)
            mid = (low + high) / 2
            if A[mid] < key
                low = mid + 1
            if A[mid] > key
                high = mid - 1
        // move A[mid..i-1] backwards such that A[i] insert A[mid] 
        for j = mid to i-1
            A[j+1] = A[j]
        A[mid] = key

 

　　但是可以发现，在查找的步骤后还需要将整个数组向后移动，而移动是线性的，每一轮都是 Θ(n)，所以最坏情况的运行时间还是 Θ(n²)。

 

2.3-7

---

　 　　

//先归并排序后二分查找
TwoNumberSum (S, x)
    mergeSort(S, 1, n)
    for j = 1 to n
        tar = x - S[j]
        j2 = BinarySearch(S, tar)
        if j2 != NIL
        break
    if j2 == NIL
        return false
    else
        return true

　　我采用的是先将S排序后，进行一轮循环查找 x-S[j]，循环不变式的终止条件是找到 x-S[j] 的值。排序采用的是归并排序，最坏情况的时间代价为 Θ(n _lgn)，而查找采用的是二分查找，最坏情况的时间代价为 Θ(_lgn)，由于查找经历了 n 轮，所以查找的总代价 Θ(n _lgn)。所以该算法最坏情况的时间代价为 Θ(n _lgn)　　

　　

　　还有一种办法，先归并排序，后利用两个指针分别指向头和尾，往中间扫描　　

TwoNumberSum (S, x)
    mergeSort (S, 1, n)
    i = 1
    j = n
    while i < j
        if A[i] + A[j] == x
            return true            
        if A[i] + A[j] < x
            i = i + 1
        if A[i] + A[j] > x
            j = j - 1
    return false

　　可以看得出来，查找的时间仅需 Θ(n)，所以时间总代价受排序时间代价的影响，为Θ(n _lgn)

　　扫描的原理很简单，先设 m_i,j  : A[i] + A[j] < S，M_i,j : A[i] + A[j] > S 。由于序列已排序，则 m_i,j ⇒∀k < j  都有 m_i,k  成立，并且 M_i,j ⇒ ∀k > i 都有 M_k,j 成立

　　

　　其实这道题是LeetCode #1 原题，还可以利用哈希存储优化时间复杂度，相关的博客链接：http://www.cnblogs.com/Bw98blogs/p/8058931.html