谈谈部分算法为什么不稳定
什么是排序稳定性？
稳定性就是指对于两个关键字相等的记录，它们在序列中的相对位置，在排序之前和排序之后没有发生改变。通俗地讲就是有两个关键字相等的数据A、B，排序前，A的位置是 i ，B的位置是 j，此时 i < j，则如果在排序后A的位置还是在B之前，那么称它是稳定的。
它的好处是，如果排序算法都是稳定的，那么第一个排序结果可以为另一个排序所用，也就是说稳定排序可以用于两个关键字的排序，比如，现在要根据英语成绩排一下大家的成绩，然后在根据数学成绩排一下大家的成绩，如果用的是稳定排序的话，就可以保证数学成绩相同的人里英语分高的人排在更前面。
而且，关键字相同的记录可能其他数据会不一致，这时交换它们就会引起问题。举个例子，如果银行有两个用户，一个是 VIP 用户，另一个是普通用户，他们都有相同的资产，如果这时候交换了他们的资产，让普通用户拥有了 VIP属性的资产，就可能会影响银行 VIP 与 普通用户的秩序。
首先给出一张在前一个博客“时间复杂度入门理解”中出现过的一副图，给出相关排序的稳定性：
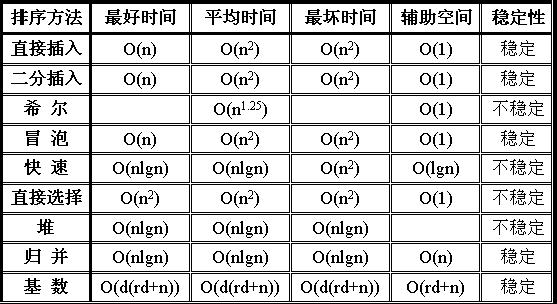
接下来，将解释图中某些排序是不稳定的的原因。
I）为什么希尔排序不稳定？
A：首先要知道 Shell 排序是基于插入排序的优化排序，插入排序每次本身只能插入一位数据，希尔排序按照步长对多个元素进行插入排序。我们知道一次插入排序是稳定的，但是同时对多组数据进行插入排序，可能不稳定了，举例：
有这样一组数：[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]
以第一轮是步长为5的希尔排序为例：
排序前：
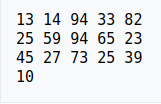
第一轮排序后 ：
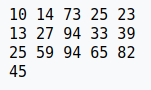
如果把第三个元素 94 换成 13，刚开始第一个 13 在 序列第一个位置，第二个 13 （也就是图中的94）在序列第三个位置，经过希尔排序第一轮后，很明显第一个 13 反而排到第二个 13 后面了，这就是同时进行多次插入排序所导致的不稳定性。
II）为什么快速排序不稳定？
A：快排的思想是先设一个中枢元素(也称是基准数，对照用)，对两遍进行排列，需要满足左边的元素都比中枢元素小，右边元素都比中枢元素大，随后对左和右的子序列也进行这样的操作（分治）。而该排序不稳定的关键就是中枢元素在调换到序列中间的时候，会破坏了原来位于中央的元素的稳定性，比如有一个序列：
6 1 2 7 9 6 4 5 10 8 ,我们定义 6 为中枢元素
进行第一轮快排后，得 6 1 2 5 4 6 9 7 10 8
这样操作就会把两个关键字同为 6 的记录交换了，算法的稳定性被破坏。所以快排是一个不稳定的排序算法，不稳定发生在中枢元素的交换时刻。
III）为什么直接选择排序是不稳定的？
A：直接选择排序的操作是这样：先在未排序的序列中选择最小的元素（或最大的元素），把它与第一个元素交换，放在第一个位置，再在剩余未排序序列中选择第二小的，与第二个元素交换，放在第二个位置...以此类推，直到所有序列排序完毕。但是，这样直接让最小元素与第 i 个位置上的元素进行交换，会破坏第一个元素的稳定性，举个例子，有一个序列如下：
33 68 46 33 25 80 19 12
第一轮排序后：
12 68 46 33 25 80 19 33
显然，第一个 33 相对于第二个 33的位置变化了，算法是不稳定的。
IV）为什么堆排序是不稳定的？
A：要说堆的结构得先说完全二叉树的结构。
完全二叉树的结构要求：
完全二叉树是一颗深度为 k ，结点总数为 n (n ≤ 2^k - 1)的二叉树，除了第 k 层外，其他第 2~(k-1) 层都达到最大结点数，第 k 层从右向左缺失若干个结点，那么这棵树为完全二叉树。[图例在这篇博客里]
完全二叉树被堆所用的性质：如果一结点的左子结点为 i ，右子结点为 i + 1，子结点 n 的父结点的位置在 i/2 (若不为整数，则向下取整) 。
接下来说堆，堆分为大顶堆和小顶堆，大顶堆要求父结点要大于它的两个子结点，小顶堆要求父结点要小于它的两个子结点。而堆排序就是移除位于第一个数据的根结点，并做堆调整的递归运算。它涉及两个关键问题：（1）如何由无序序列建“初始堆”？ （2）输出堆顶后，如何进行堆的筛选（调整）？
建立堆的操作如下：
（1）以给定的无序序列为基础建立一个完全二叉树
（2）由于叶子结点本身肯定满足堆结构，那么从第一个非叶子结点（比如第一个叶子结点的父结点）开始向上调整，重复（2）步骤
当然你也可以定一个顶点为堆，然后往这个堆里添加元素，但是这个方式建堆的时间复杂度是 O(nlgn)，前一个方法建堆的时间复杂度是 O(n)
输出堆顶后，此时需要维护堆，操作如下：
（1）堆顶与堆尾交换并删除堆尾，被删除的堆尾的元素就是输出过的元素
（2）把当前堆顶向下调整，直到满足构成堆的条件，重复（2）步骤
很显然，在建立堆的调整步骤里，由于关键字相同的两个记录位置并不会被调换，所以建堆的时候是稳定的。但是，在堆顶与堆尾交换的时候两个相等的记录在序列中的相对位置就可能发生改变，这就影响其稳定性了。
注意
排序算法是否为稳定的是由具体算法决定的，不稳定的算法在某种条件下可以变为稳定的算法，而稳定的算法在某种条件下也可以变为不稳定的算法。比如冒泡，若让交换的条件改成 r[j] >= r[j+1],两个相等的记录就会交换位置，从而变成不稳定的算法。
有很多办法可以将任意排序算法变成稳定的，但是，往往需要额外的时间或者空间。所以我们在讨论的排序算法稳定性的时候，往往是在不需要额外的时间或空间的前提下才进行讨论的。
