散列的概念、构造散列函数以及解决冲突的方法
定义
散列表(Hash Table,也称哈希表),是一种根据键(Key)而直接访问在内存存储位置的数据结构。也就是说,它通过计算一个关于键值的函数,将所需查询的数据映射到表中一个位置来访问记录,这加快了查找速度。这个映射函数称为散列函数,存放记录的数组称做散列表。
概念
1、若其关键字为k,则其值存放在 f(k) 的存储位置上。因此不需要比较即可直接取得所查记录。称这个对应关系 f 为散列函数,按照这个思想建立的表叫散列表。
2、对不同的关键字可能得到同一个散列地址,即k1 != k2,而 f(k1) = f(k2),这种情况称之为冲突(Collision)。具有相同函数值的关键字对该散列函数来说称为同义词(Synonym)。
3、综上所述,根据散列函数 f(k) 和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或者是散列,所得的存储位置称散列地址。
4、若对于关键字集合中的任一个关键字,经散列函数映象到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就是使关键字经过散列函数得到一个“随机的地址”,从而减少冲突。
Hash函数的构造方法
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快定位。
影响哈希查找效率的一个重要因素是哈希函数本身。当两个不同的数据元素的哈希值相同时,就会发生冲突。为减少发生冲突的可能性,哈希函数应该将数据尽可能分散地映射到哈希表的每一个表项中。
下面是几种定址方法:
1、直接定址法:取关键字或关键字的某个线性函数值为散列地址。即 Hash(k) = k 或 hash(k) = ak+b,其中 a b为常数(这种散列函数叫做自身函数)
2、数字分析法:假设关键字是以r为基的数,并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。比如有一组value1=112233,value2=112633,value3=119033,针对这样的数我们分析数中间两个数比较波动,其他数不变。那么我们取key的值就可以是key1=22,key2=26,key3=90。
3、平方中取法:取关键字平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况,取其中的哪几位也不一定合适,而一个数平方后的中间几位数和数的每一位都相关,由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。
4、折叠法:将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址。举个例子,比如value=135790,要求key是2位数的散列值。那么我们将value变为13+57+90=160,然后去掉高位“1”,此时key=60,这就是他们的哈希关系,这样做的目的就是key与每一位value都相关,来做到“散列地址”尽可能分散的目地。
5、随机数法
6、除留余数法:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址,即hash(k) = k mod p, p <= m。不仅可以对关键字直接取模,也可在折叠法、平方取中法等运算之后取模。对p的选择很重要,一般取素数或m,若p选择不好,容易产生冲突。
处理冲突的办法
为了知道冲突产生的相同散列函数地址所对应的关键字,必须选用另外的散列函数,或者对冲突结果进行处理。而不发生冲突的可能性是非常之小的,所以通常对冲突进行处理。常用的办法如下:
1、链接地址法:
将哈希值相同的数据元素存放在一个链表中,在查找哈希表的过程中,当查找到这个链表时,必须采用线性查找方法。
举个例子:关键字为{ 41,26,68,15,44,6,36,38,12,51}的一组数据插入散列表,并假定以关键字除以13的余数为散列函数的法则。
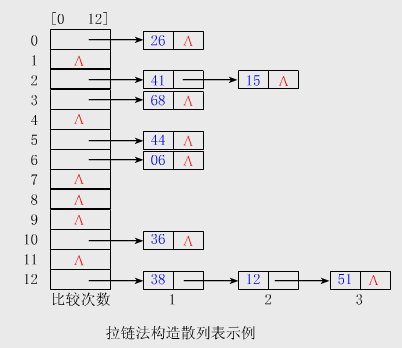
2、开放定址法:
公式: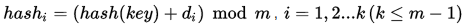
其中 hash(key) 为散列函数,m 为散列表长,di 为增量序列,i为已发生的冲突次数。
增量序列有下面三种取法:
I)di = 1,2,3...m-1 称为线性探测(Linear Probing)即 di = i,或者为其他线性函数。相当于逐个探测存放地址的表,如果为空,把数据放在空的位置。
II)di = (+ 1^2) or (- 1^2),(+ 2^2) or (- 2^2) ... + (k^2) or (- k^2) 称为平方探测(Quadratic Probing) 相对于线性探测,相当于发生冲突时探测间隔 di = i^2 个单元的位置是否为空,如果为空则把数据放到空的位置。
III)di = 伪随机数序例,称为伪随机探测。
给出一个用线性探测填装一个散列表的过程:
关键字为{89,18,49,58,69}插入到一个散列表中的情况,此时线性探测的方法是取 di = i,并假定取关键字除以10的余数为散列函数法则。
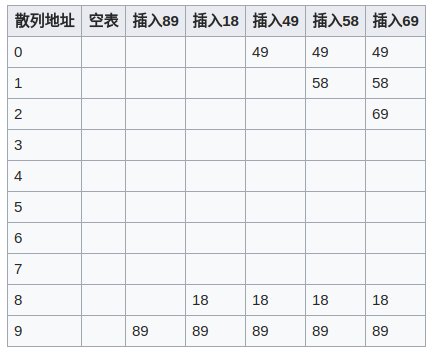
第一次冲突发生在填装49的时候。地址为9的单元已经填装了89这个关键字,所以取 i = 1,往下查找一个单位,发现为空,所以将49填装在地址为0的空单元。第二次冲突则发生在58上,取 i = 2,往下查找两个单位,将58填装在地址为1的空单元。69同理。
表的大小选取至关重要,此处选取10作为大小,发生冲突的几率就比选择质数11作为大小的可能性大。越是质数,mod取余就越可能均匀分布在表的各处。
3、再散列:
公式: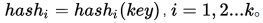
Hashi 是某些散列函数。即上次散列发生冲突时,利用该冲突地址进行再散列,直到冲突不再发生。该办法不易发生分布不均匀的情况,但增加了计算时间。
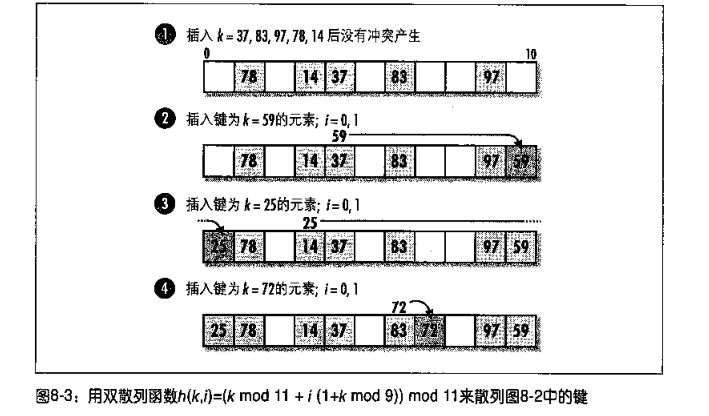
举个例子,现有一序列 <37, 83, 97, 78, 14, 59, 25, 72>,画出构建哈希表的过程,哈希函数是 hash(i) = i mod 11,解决冲突的办法是再散列( mod 9)。
前五个插入都没有问题。当插入 59 时,h(59,0) = (59 mod 11 ) mod 11 = 4,位置 4 与 37 冲突,继续计算。冲突 1 次,i = 1,h(59,1) = (59 mod 11 + 1*(1+59 mod 9)) mod 11 = 10,位置 10 空,59 插入到位置 10 。如果再冲突,那么 i = 2,继续计算,以此类推。25 和 72 类似。
ASL成功/不成功 的求法
关于哈希表求查找成功与查找成功时的平均查找长度的题目,我觉得这篇博客说的不错。


