LeetCode #275. H-Index II 数组 二分查找

Description

Given an array of citations sorted in ascending order (each citation is a non-negative integer) of a researcher, write a function to compute the researcher's h-index.

According to the definition of h-index on Wikipedia: "A scientist has index h if h of his/her N papers have at least h citations each, and the other N − h papers have no more than h citations each."

Example:

Input: citations = [0,1,3,5,6]
Output: 3 
Explanation: [0,1,3,5,6] means the researcher has 5 papers in total and each of them had 
             received 0, 1, 3, 5, 6 citations respectively. 
             Since the researcher has 3 papers with at least 3 citations each and the remaining 
             two with no more than 3 citations each, her h-index is 3.

Note:
If there are several possible values for h, the maximum one is taken as the h-index.

Follow up:

  • This is a follow up problem to H-Index, where citations is now guaranteed to be sorted in ascending order.
  • Could you solve it in logarithmic time complexity?



思路

解法一

想要理解这个算法，必须要弄懂我之前写 #274 的解法二。

看到已排序序列和 O(lgn) 就能联想到这道题的解题方法大概率是二分查找，仔细分析后发现这道题还是二分查找中比较难的那一类，因为要查找的目标值（H-Index）一直在变化。

274题的解法二中我们将数组是从大到小排序，每个位置的 h = 索引值，在这道题里并不适用，所以要重新设计每个位置的 h。

一个比较好的办法是，让每个位置的 h = length - 索引值，这样的话 h 就是一个降序序列，而且很方便获得某个位置的 h，如下图。原理很简单：如果一个位置上的 h 是题目想要的 H-Index，那么就有 citations[0..h-1] ≤ h 且 citations[h..n] ≥ h。

例子

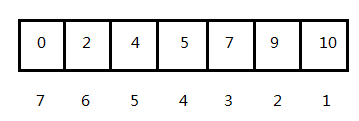
然后，在二分查找的过程中，如果某个 h 值满足条件（即 h 值 ≤ 它对应的值，比如元素 5 在的位置 h = 4，此时有 4 篇论文的引用 ≥ 4，其余 len - h = 3 篇论文的引用 ≤ 4），我们就可以直接到前半部分继续查找满足条件且更大的 h 值；同理，如果 h 值不满足条件（即 h 值 > 它对应的值），我们就到后半部分继续查找。

对于 corner case，比如 [], [0], [1, 2] 这样的数据，我们需要重新设计二分查找中的判断条件，比如将 while 的条件改成 left ≤ right，每次右移时将 right 赋值为 mid - 1 而不是 mid 以避免死循环。

时间复杂度：O(lgn)
空间复杂度：O(1)

耗时 20 ms, Memory 10.2 MB, ranking 86.57%

class Solution {
public:
    int hIndex(vector<int> &citations) {
        int len = citations.size();
        int left = 0;
        int right = len - 1;  // set right as len-1 so as to pass [], [0]

        while (left <= right) {
            int mid = left + (right - left)/2;
            int h = len - mid;

            if (h <= citations[mid]) {
                right = mid - 1;  // there is forever loop if right = mid
            } else {
                left = mid + 1;
            }
        }

        // after while, left = mid. if there is a solution, 
        // then len - left = correct h, and left = right + 1
        return len - left;
    }
};



深入理解二分查找算法

利用左闭右开思想，我们可以把 left 和 right 分别设为 0 和 n。当每次扫描完一个元素时，如果符合要求，则将 right 移动到该元素的位置上，表示该搜索区间已去除该元素，此后不再扫描它；否则将 left 移动到 mid + 1 的位置，搜索区间缩小至 [mid + 1, right)，同样将该元素踢出搜索区间。当 left = right 时，说明搜索区间为空，可以终止搜索了。

这么做的好处是，不必再为代码哪里冒出来的 +1 -1 < ≤ return 所烦恼，同时也不必烦恼 left 和 right 哪一个才是最后的正确结果，大大降低代码出错率。

该算法相当于 c++ STL中的 std::lower_bound()，应该可以处理绝大部分二分查找的问题，也可以处理特殊的 corner case，比如本题的 [0, 0, 0] 和 [1, 2]。但是要注意，该通用步骤可能无法处理《LeetCode Binary Search Summary 二分搜索法小结》中提到的 target 变化的第五类题型。这类题型里的 target 可能和 right 有关，如果把 right 设置成 n 的话，再次访问 nums[right] 时可能会数组越界，所以在这类题型里需要把 right 初始化为 n-1 。

算法的通用步骤如下：

  • left = 0, right = n
  • while(left < right)
  • mid = (left+right)/2
  • left = mid+1
  • right = mid

最后 jump 出去后，left 和 right 必相等，任选其中一个就是我们想要的答案。

根据这个思路，我们重写本题的二分查找算法

class Solution {
public:
    int hIndex(const vector<int> &citations) {
        int len = citations.size();
        int left = 0;
        int right = len;  // set right as len-1 so as to pass [], [0]

        while (left < right) {
            int mid = left + (right - left)/2;
            int h = len - mid;

            if (h <= citations[mid]) {
                right = mid;  // there is forever loop if right = mid
            } else {
                left = mid + 1;
            }
        }

        return len - left;
    }
};



参考



posted @ 2020-04-18 19:49  bw98  阅读(192)  评论(0)  编辑  收藏  举报