高精度压位
唔...很久没讲算法之类的了...
这次讲一个我认为比较黑科技的东东——高精度压位。
普通高精度
先从普通的高精度来讲起。
高精度实际上是将每一位上的数看做一个数放在数组里，再模拟人工计算。
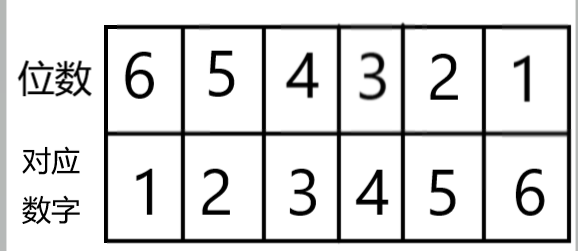
实际数为 123456 (本文最低位(这里就是'6'这个数字) 位数标为1，原因是适应实际运算最高位会改变，而下标不会往负方向减少，即下标没有负的)
这个就是将一个数处理后的样子，之后就可以模拟人工计算将答案算出。
高精度压位
然后就是压位技巧啦，其实压位技巧很简单...这样考虑，我们是用数组保存每一个数的，但是这个数组其实可以保存更大的数，而不是一个一位数。由此发现，压位优化了空间。
所以，压位是什么，画图啦~。
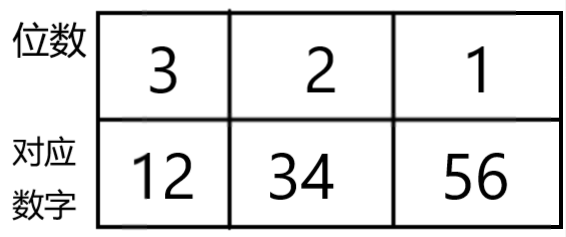
实际数： 12 34 56 （两个两个看便是压位）
这就是压位，将一个一位数，变成两位数，压在同一个下标当中。
如何简单的理解压位呢，不如将这个数，看成100进制，这样就是两位数了。
那压位之后的高精度，有什么变化么？
对于计算而言，基本没有，因为在计算过程中只是将模数改为100而已（原来是10，模数即过程中考虑进位时需要取模）。
对于输出而言，有一个比较明显的变化 补0输出。
举个栗子嘿嘿，问问神奇海螺（某博客有趣的小梗，出自海绵宝宝）？
如这样一个数要输出 ：
50002005
将其压位（压为两位数）：
50 00 20 05
而数组里保存的可没有前导0，它是这样的：
50 0 20 5
此时如果直接输出就与原始数不同了，所以除了最后位(即从左往右数第一位非0数） 外，都要补0。
例题：
这是一个很常见的dp，先不考虑高精度。
dp[i][j] 表示到达i，j的方案数。
考虑将题目中给的矩阵a[i][j]赋值为1表示不可以走。
方程就是 dp[i][j]=dp[i-1][j]+dp[i][j-1] (a[i][j]!=1要可以走才行，对于a[i-1][j]或a[i][j-1]是否为1无需考虑，因为dp[i-1][j],dp[i][j-1]会是0，对答案不影响)
就是可以从左往右走，也可以从上往下走。
题目要求保留20位，可是20位已经超过longlong了。
正常想法就是高精度了，可是，试试用压位简化代码。
设dp[i][j][0]表示答案的前10位，dp[i][j][1] 表示答案的后10位，这样合起来就是20位。 (注意10位需要longlong int 为 10^9)
先不考虑进位那么
dp[i][j][0]=dp[i-1][j][0]+dp[i][j-1][0]；
dp[i][j][1]=dp[i-1][j][1]+dp[i][j-1][1]；
再考虑进位，dp[i][j][1]是最低位，要向dp[i][j][0] 进位。
进位过程就是dp[i][j][1]%=1e10 dp[i][j][0]+=dp[i][j][1]/1e10 (1e10为10^10,就是压10位)
这个就是压位了，注意压位不一定只像前文说的压成100，当然1000 10000等等都是可以压的。
