NOIP2016 T4 魔法阵暴力枚举+前缀和后缀和优化

想把最近几年的NOIP T4都先干掉，就大概差16年的，所以来做一做。

然后这题就浪费了我一整天QAQ...果然还是自己太弱了QAQ

点我看题

还是pa洛谷的...

题意：给m个物品，每个物品有一个不超过n的数xi。

如果存在四元组 (a,b,c,d)满足

① x_a<x_b<x_c<x_d

　　②　　 x_b-x_a=2(x_d-x_c)

③ x_b-x_a<(x_c-x_b)/3

辣么这个四元组是有效的，问每个物品分别作为有效四元组中 a，b，c，d 几次

思路：16年是第一次参加的noip啊...结果炸的挺惨的，比赛的时候这题没多少时间打了，就草草打了一个暴力优化，结果细节没考虑挂掉了。

今天再来写的时候先敲了暴力，一个简单的暴力优化可以水到85分，所以真的是暴力出奇迹啊=v=

辣正解捏，不得不说这题的数学成分实在太高，我想了整整一个下午都没搞懂，但其实真的不是很难吧...

我们可以这样去想，把每一个物品的数字都抽象为一个数轴上的点的坐标。

然后画图。

可以这样考虑，设x_d-x_c=i 则 x_b-x_a=2*(x_d-x_c)=2*i

把化简的二式带入三式得： 6*i<x_c-x_b 设6*i+k=x_c-x_{b ( 就是把差的部分补上去，这个姿势貌似还挺有用)}

这样的话就可以画图了，由一式条件和化简后的式子可以得到这样的图

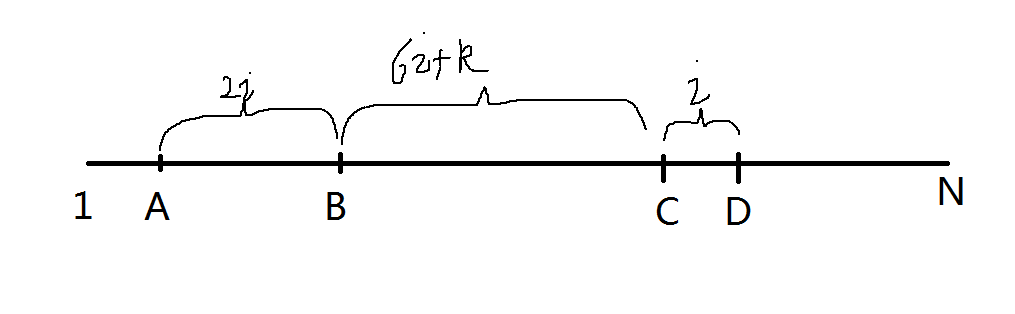
图丑就别喷了... 所以 AD=9i+k 所以 i 的取值范围也可以得到 1≤i≤n/9 (准确来说 i 要比n更小，不过没什么影响)

画完图是不是清晰了一点(其实并没有啊)

然后我萌就可以这样想了，如果知道了 i 和 A 就可以得到 B 如果知道 i 和 C 就可以得到 D 但是如果仅知道某两项是得不到其他的。

我萌把A和B看成一个整体，把C和D看成一个整体，并分别求答案。

我萌枚举 i ，然后枚举 A 这样可以算出 B，同时我萌可以知道 C 和 D的最小位置即当 k=1 时 C=A+8i+1，D=A+9i+1, 知道这个最小位置有什么用？

因为知道A的答案=数字为B的物品个数*数字为C的物品个数*数字为D的物品个数

而对于任意k，如果存在数字C的位置有物品且D的位置有物品，辣么很显然数字为C的物品个数*数字为D的物品个数可以通过枚举A的过程中利用后缀和进行累积，然后又因为要后缀和，所以A就得从后往前枚举。

B的答案类似，在A进行求答的时候可以一起求了。

B的答案=数字为A的物品个数*数字为C的物品个数*数字为D的物品个数

辣CD为一个整体的时候捏，类比啊，一样的，但是发现数字为A的物品个数*数字为B的物品个数累积的时候是前缀和了，所以C的枚举就是从前往后。

一道很棒的题，很棒的数学题...(困惑了我好久，看题解还看不懂！！)

 1 var n,m:longint;
 2     a,id,num:array[0..50000]of longint;
 3     l:array[0..50000]of longint;
 4     i,j,k,d:longint;
 5     z:longint;
 6     numab,numcd:longint;
 7     sum:array[0..50000,0..4]of longint;
 8 begin
 9   read(n,m);
10   for i:=1 to m do
11   begin
12     read(a[i]);
13     inc(num[a[i]])
14   end;
15   for i:=1 to (n div 9) do
16   begin
17     numcd:=0;
18     for j:=n-(9*i+1) downto 1 do
19     begin
20       numcd:=numcd+num[j+8*i+1]*num[j+9*i+1];
21       inc(sum[j,1],num[j+2*i]*numcd);
22       inc(sum[j+2*i,2],num[j]*numcd);
23     end;
24     numab:=0;
25     for j:=8*i+2 to n-i do
26     begin
27       numab:=numab+num[j-8*i-1]*num[j-6*i-1];
28       inc(sum[j,3],num[j+i]*numab);
29       inc(sum[j+i,4],num[j]*numab);
30     end;
31   end;
32   for i:=1 to m do
33   begin
34     for j:=1 to 4 do
35     write(sum[a[i],j],' ');
36     writeln;
37   end;
38 end.

NOIP2016 T4

转c++后重新写了一遍这题，有了更好的理解代码一起pia上来

 1 #include<cstdio>
 2 #define ll long long
 3 using namespace std;
 4 ll ans[40050][5];
 5 int a[40050],num[15050];
 6 int main(){
 7     int n,m;
 8     scanf("%d%d",&n,&m);
 9     for (int i=1;i<=m;i++){
10         scanf("%d",&a[i]);
11         num[a[i]]++;
12     }
13     for (int t=1;t<=n/9;t++){
14         ll sum=0;
15         for (int i=8*t+2;i<=n-t;i++){
16             sum+=1ll*num[i-8*t-1]*num[i-6*t-1];
17             ans[i][3]+=sum*num[i]*num[i+t];
18             ans[i+t][4]+=sum*num[i]*num[i+t];
19         }
20         sum=0;
21         for (int i=n-7*t-1;i>2*t;i--){
22             sum+=1ll*num[i+6*t+1]*num[i+7*t+1];
23             ans[i][2]+=sum*num[i]*num[i-2*t];
24             ans[i-2*t][1]+=sum*num[i]*num[i-2*t];
25         }
26     }
27     for (int i=1;i<=m;i++){
28         for (int j=1;j<=4;j++)
29         printf("%lld ",ans[a[i]][j]/num[a[i]]);
30         printf("\n");
31     }
32     return 0;
33 }
34 /* 
35 条件① Xa<Xb<Xc<Xd
36     ② Xb-Xa=2(Xd-Xc)
37     ③ Xb-Xa<(Xc-Xb)/3
38     可以发现Xd-Xc是一个最小单位
39     设 t=Xd-Xc;
40     ②得Xb-Xa=2t
41     ③得2t<(Xc-Xb)/3 即6t<Xc-Xb 
42     粗略的画图
43     --------------------
44      A B------C  D   
45      --- >6t  ----
46       t        2t
47     D最大是n A最小是1
48     所以t的取值就是
49     1<=t<=(n-1)/t
50     粗略的
51     1<=t<=n/t 因为数组开大后溢出没有任何影响
52     于是枚举t 再枚举C
53     D的位置就得到了
54     而因为BC之间只要大于6t就行。
55     所以设C1<C2 D1<D2
56     C1 D1所能匹配的A B C2 D2 也可以
57     于是满足了前缀和
58     只要往后枚举C的时候把上一个C的A B组数保存着累加就好了
59     A B同理，枚举 B，A确定 C D变成了后缀和。
60     画图把B C的取值范围算一下即可 
61 */

NOIP2016 T4

果然自己真的要多做题啊QAQ

posted @ 2017-08-12 22:00 Bunnycxk 阅读(989) 评论(2) 编辑收藏举报

刷新页面返回顶部

Bunnycxk

NOIP2016 T4 魔法阵 暴力枚举+前缀和后缀和优化

公告

NOIP2016 T4 魔法阵暴力枚举+前缀和后缀和优化