高级搜索题集

题集转自以下链接：

https://blog.csdn.net/shahdza/article/details/7986044

胜利大逃亡(续) HDU - 1429

题意：就是二维地图，有障碍；重点有门，和钥匙（用于开门）。

理解：因为找钥匙，这个解答路径可能会走回头路。

思路：第一遍，因为有时间限制，并且20*20；所以简单bfs，然后MLimit了。感觉就是重复存储点在队列。

那么难点就在于判重了。因为走回头路，简单二维判重肯定不行。

回想和之前炮台那题，因为子弹的原因也是走回头路，所以判重数组多加了一个时间维度。

这题关键因素是钥匙，所以加一个钥匙拥有状态的判重，就ac了。（用2进制状态压缩，这里因为a-j，所以数组开个1024就够了。）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

int n,m,t;
char ditu[21][21];
bool vis[1025][21][21];
int Sx,Sy,Fx,Fy;

int xx[] = {0,0,1,-1};
int yy[] = {1,-1,0,0};

struct node{
    int x,y,step,k=0;
    node(int a,int b,int c,int d):x(a),y(b),step(c),k(d) {};
};


bool bfs(){
    memset(vis,false,sizeof vis);
    queue<node> q;q.push(node(Sx,Sy,0,0));vis[0][Sx][Sy] = true;
    while(!q.empty()){
        node p = q.front();q.pop();
        for(int i=0;i<4;i++){
            int x = p.x+xx[i],y = p.y+yy[i];
            if(x<0||x>=n||y<0||y>=m||ditu[x][y]=='*'||p.step+1>=t) continue;
            int step = p.step + 1,k = p.k;
            if(ditu[x][y]>='A'&&ditu[x][y]<='Z'&&!(p.k&(1<<ditu[x][y]-'A'))) continue;
            if(ditu[x][y] == '^') {cout<<step<<endl;return true;}
            if(ditu[x][y]>='a'&&ditu[x][y]<='z') k |= 1<<(ditu[x][y]-'a');
            if(vis[k][x][y]) continue;
            q.push(node(x,y,step,k));vis[k][x][y] = true;
        }
    }
    return false;
}

int main()
{
    while(cin>>n>>m>>t){
        for(int i=0;i<n;i++)for(int j=0;j<m;j++){
            char ch = getchar();while(ch==' '||ch=='\n') ch = getchar();
            ditu[i][j] = ch;
            if(ch=='^') Fx = i,Fy = j;
            else if(ch=='@') Sx = i,Sy = j;
        }

        if(!bfs()) puts("-1");
    }
    return 0;
}

View Code

这题给我启发就是，判重作用在于剪枝，避免重复的入队操作。那么关键在于什么？关键在于点状态更新，并且取决于什么要素关键，炮台那题，因为子弹原因，时间是关键。这题因为门的原因，钥匙是关键。所以添加关键要素的判重数组是解题关键。

Key Task HDU - 1885

题意与上题一样。但是地图大小和钥匙，门出口数量不同。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <map>

using namespace std;

int n,m;
char ditu[101][101];
bool vis[17][101][101];
int Sx,Sy,Fx,Fy;

int xx[] = {0,0,1,-1};
int yy[] = {1,-1,0,0};

struct node{
    int x,y,step,k=0;
    node(int a,int b,int c,int d):x(a),y(b),step(c),k(d) {};
};

int mp[5];

bool bfs(){
    memset(vis,false,sizeof vis);
    queue<node> q;q.push(node(Sx,Sy,0,0));vis[0][Sx][Sy] = true;
    while(!q.empty()){
        node p = q.front();q.pop();
        for(int i=0;i<4;i++){
            int x = p.x+xx[i],y = p.y+yy[i];
            if(x<0||x>=n||y<0||y>=m||ditu[x][y]=='#') continue;
            int step = p.step + 1,k = p.k;
            if(ditu[x][y] == 'X') {cout<<"Escape possible in "<<step<<" steps."<<endl;return true;}
            if(ditu[x][y]>='A'&&ditu[x][y]<='Z'&&!(p.k&(1<<mp[ditu[x][y]-'A']))) continue;
            if(ditu[x][y]>='a'&&ditu[x][y]<='z') k |= 1<<mp[ditu[x][y]-'a'];
            if(vis[k][x][y]) continue;
            q.push(node(x,y,step,k));vis[k][x][y] = true;
        }
    }
    return false;
}

int main()
{
    mp['B'-'A'] = 0,mp['Y'-'A'] = 1,mp['R'-'A'] = 2,mp['G'-'A'] = 3;
    while(cin>>n>>m&&n&&m){
        for(int i=0;i<n;i++)for(int j=0;j<m;j++){
            char ch = getchar();while(ch==' '||ch=='\n') ch = getchar();
            ditu[i][j] = ch;
            if(ch=='X') Fx = i,Fy = j;
            else if(ch=='*') Sx = i,Sy = j;
        }

        if(!bfs()) puts("The poor student is trapped!");
    }
    return 0;
}

View Code

扩展思考：我这里想到如果钥匙并非永久产品而是一次性，那该怎么办？

我感觉难点可能在于不止走一次回头路。

我一开始能想到就是：像多重背包操作一样，将问题转化为0-1，多个相同门和钥匙，对应将他们分类成不同颜色。额，好像不行，因为你不清楚那个钥匙对应哪个门即为最优。。。。

那判重函数多加一维度，有什么颜色钥匙，并且多一个钥匙数量的维度。

超级密码HDU - 1226

算法：BFS

思路：BFS向下操作，*进制数+构成数然后对N求余得到的余数，因为是要正整数倍，所以当余数为0则为答案。

K1%N = K2%N；（K1*C+M）%N = （K2*C+M）%N ；所以余数可以作为判重点。相同余数不需要重复入队。

用数组记录答案长度，因为BFS是有层次性，所以超过500就可以判负了。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <map>

using namespace std;

int N,C,M;
int yS[17],ySlen;
int vis[5005],pre[5005],ans[5005],cnt[5005];

void init(){
    memset(vis,0,sizeof vis);
    memset(cnt,0,sizeof cnt);
    memset(pre,-1,sizeof pre);
    scanf("%d%d%d",&N,&C,&M);
    for(int i=0;i<M;i++){
        char ch = getchar();while(ch == ' '|| ch == '\n') ch = getchar();
        if(ch>='0'&&ch<='9') yS[i] = ch - '0';
        else yS[i] = ch - 'A' + 10;
    }
    sort(yS,yS+M);
    ySlen = unique(yS,yS+M) - yS;
}

void showAns(int num){
    if(num == -1) return ;
    showAns(pre[num]);
    if(ans[num]<10) printf("%d",ans[num]);
    else printf("%c",ans[num] - 10 + 'A');
}

bool solve(){
    queue<int> q;
    for(int i=0;i<ySlen;i++){
        if(!yS[i]) continue;
        int tnt = yS[i] % N;
        if(vis[tnt]) continue;
        vis[tnt] = 1;cnt[tnt] = 1;
        ans[tnt] = yS[i];
        if(!tnt) return true;
        q.push(tnt);
    }
    while(!q.empty()){
        int now = q.front();q.pop();
        if(cnt[now]>500) return false;
        for(int i=0;i<ySlen;i++){
            int tnt  = (now*C + yS[i]) % N;
            if(vis[tnt]) continue;
            vis[tnt] = 1;cnt[tnt] = cnt[now] + 1;
            ans[tnt] = yS[i];pre[tnt] = now;
            if(!tnt) return true;
            q.push(tnt);
        }
    }
    return false;
}

int main()
{
    int _;scanf("%d",&_);
    while(_--){
        init();
        if(!N) {if(!yS[0]) puts("0");else puts("give me the bomb please");}
        else{
            if(!solve()) puts("give me the bomb please");
            else showAns(0),puts("");
        }
    }
    return 0;
}

View Code

Different DigitsHDU - 1664

算法：数论+BFS

思路：感觉这题集出得挺不错，每道题总与上一道题有关联。这一题和上一题一样，也是求N的正整数倍。所以也是余数下手。

但是这题巧妙在于，最优解是，答案需尽量少不同数字构成且最小。

这里牵扯的数论就是：

很好理解：求10进制的余数，（*10+1）MOD，因为只加一个数字的求余存在一个循环，存在0则为答案。余数相同，就互减得到答案，互减将余数减掉就是N的整数倍了。

所以一个整数一定存在一个正整数倍的数，且由0和1的数构成。

所以，两不同数字就构成本题答案；

那么这题剩下就是求一个最优最小解，即不同数字的数量相同求最小。

分两层，第一层只用一个数叠加求，得到答案就是最优。得不到去第二层，循环从不同两个数字组合求出答案。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <map>

using namespace std;

const int inf = 2e9;

int N,ansLen;
bool vis[65536];
string ans,res;

bool gO(int x){
    memset(vis,false,sizeof vis);
    int tmp = 0;res = "";
    while(1){
        tmp = (tmp*10+x) % N;
        if(vis[tmp]) return false;
        vis[tmp] = true;
        res += '0' + x;
        if(!tmp){
            if(ansLen == inf||ans.length()>res.length()){
                ans = res;ansLen = res.length();return true;
            }
            return false;
        }
    }
}

int val[65536],pre[65536],cnt[65536];

void getAns(int x){
    if(x==-1) return ;
    getAns(pre[x]);
    res += '0' + val[x];
}

bool gT(int x,int y){
    memset(vis,false,sizeof vis);
    memset(pre,-1,sizeof pre);
    memset(cnt,0,sizeof cnt);
    queue<int> q;
    int fk,num[2]={x,y};
    if(x) { fk = x%N;vis[fk] = true,val[fk] = x,cnt[fk] = 1;q.push(fk); }
    fk = y%N; if(!vis[fk]) {vis[fk] = true,val[fk] = y,cnt[fk] = 1;q.push(fk);}
    while(!q.empty()){
        int now = q.front();q.pop();
        if(cnt[now]>ansLen) return false;
        for(int i=0;i<2;i++){
            fk = (now*10 + num[i]) % N;
            if(vis[fk]) continue;
            vis[fk] = true,val[fk] = num[i],cnt[fk] = cnt[now] + 1,pre[fk] = now;
            if(!fk){
                res = "";getAns(0);
                if(ansLen==inf||ans.length()>res.length()||(ans.length()==res.length()&&res<ans)){
                    ans = res;ansLen = res.length();
                    return true;
                }
                return false;
            }
            q.push(fk);
        }
    }
    return false;
}

int main()
{
    while(cin>>N&&N){
        int flag = 0; ansLen = inf;ans = "";
        for(int i=1;i<10;i++) if(gO(i)) flag = 1;
        if(flag) {cout<<ans<<endl;continue;}
        for(int i=0;i<10;i++) for(int j=i+1;j<10;j++) gT(i,j);
        cout<<ans<<endl;
    }
    return 0;
}

View Code

Pusher HDU - 2821

算法：枚举+dfs（简单模拟）

题意：类似手机游戏，一副25*25的地图，有多个障碍物，障碍物由字母表示，a为一方块，b为内嵌的2方块，以此类推。

球体，要选取一个地方起步（这里我用全地图枚举），进行弹射必须有一个空格当空隙。

起步后，方向不变，直到撞到方块才停下，且推方块向后一步，方块数减一，剩余方块积累到后一步。后一步如果是地图外，则起步方块消失。

如果球飞出地图，则失败。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <map>

using namespace std;

int n,m;
int ditu[26][26],sum;

int xx[4] = {0,0,1,-1};
int yy[4] = {1,-1,0,0};
char dire[5] = "RLDU";

int len;
char ans[2500];

void init(){
    sum = 0,len=0;
    memset(ditu,0,sizeof ditu);
    for(int i=0;i<n;i++)for(int j=0;j<m;j++){
        char ch = getchar();
        while(ch==' '||ch=='\n') ch = getchar();
        if(ch>='a'&&ch<='z') ditu[i][j] += ch - 'a' + 1, sum+= ditu[i][j];
    }
}
bool check(int a,int b,int c){
    int x = a + xx[c] , y = b + yy[c];
    if(x<0||x>=n||y<0||y>=m||ditu[x][y]!=0) return false;
    return true;
}

int check3(int x,int y){
    if(x<0||x>=n||y<0||y>=m) return 0;
    if(ditu[x][y]!=0) return 1;
    return 2;
}

bool check2(int &a,int &b,int c){
    while(1){
        a += xx[c],b += yy[c];
        int tnt = check3(a,b);
        if(tnt==0) return false;
        if(tnt==1) return true;
    }
}

bool dfs(int x,int y,int z){
    if(z==0) return true;
    for(int i=0;i<4;i++){
        if(!check(x,y,i)) continue;
        int a = x,b = y;
        if(!check2(a,b,i)) continue;
        //cout<<x<<" "<<y<<" "<<a<<" "<<b<<" "<<z<<endl;
        bool flag = false;
        if(check3(a+xx[i],b+yy[i])!=0) flag = true;
        int fk = ditu[a][b],fkk,c;
        if(flag){
            fkk = ditu[a+xx[i]][b+yy[i]];
            ditu[a+xx[i]][b+yy[i]] += fk - 1;
            c = z - 1;
        }else c = z - fk;
        ditu[a][b] = 0;
        ans[len++] = dire[i];
        if(dfs(a,b,c)) return true;
        len--;
        ditu[a][b] = fk;
        if(flag) ditu[a+xx[i]][b+yy[i]] = fkk;
    }
    return false;
}

int main()
{
    while(cin>>m>>n){
        init();
        //cout<<sum<<endl;
        //for(int i=0;i<n;i++){for(int j=0;j<m;j++) cout<<ditu[i][j]<<" ";cout<<endl;}
        int cp = 1;
        for(int i=0;i<n&&cp;i++)for(int j=0;j<m&&cp;j++) if(ditu[i][j]==0&&dfs(i,j,sum)) {
                printf("%d\n%d\n",i,j);
                ans[len] = '\0';cout<<ans<<endl;
                cp = 0;
        }
    }
    return 0;
}

View Code

Tempter of the Bone IIHDU - 2128

算法：BFS/DFS

题意：就是给一个有障碍的地图，图上有炸弹推，经过就可以捡上，不过只能捡一次。炸弹可以炸墙，不过算一步。

判重就简单的3维，坐标加炸弹。

BFS

这里我BFS，直接模拟，找到答案直接输出，然后wrong了。

后面看别人代码，得知原因，因为，我直接将炸开炸弹，与进入墙体两步，结合在一层进行模拟；

容易导致BFS跨步错误，就像之前做过的一道题，情侣被鬼追，G - Nightmare Ⅱ HDU - 3085 。这题我在kuangbin题集做了解析。

这里类似2步走，第二步vis标记会导致其他第一步入队而出现答案错误，wrong。

这里我是看别人代码学的操作，将vis移到出队再加，然后答案，通过ans记录，并进行求最短剪枝。这里就相当于将vis标记放到下一层去判断，虽然会增加入队冗余，但是ans优化也减了一部分。

一开始码的时候不知道这样对不对？不管先试了再说。然后就AC了。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <map>

using namespace std;

const int inf = 2e9;

int n,m,ans;
int Sx,Sy;

char ditu[9][9];
bool vis[9][9][600];

int xx[] = {1,-1,0,0};
int yy[] = {0,0,1,-1};

void init(){
    memset(vis,false,sizeof vis);
    ans = inf;
    for(int i=0;i<n;i++)for(int j=0;j<m;j++){
        char ch = getchar();while(ch==' '||ch=='\n') ch = getchar();
        ditu[i][j] = ch;
        if(ch=='S') Sx = i,Sy = j;
    }
}

struct node{
    int x,y,step,exp;
    bool state[9][9];
    node(int a,int b,int c,int d):x(a),y(b),step(c),exp(d) {
        memset(state,false,sizeof state);
    };
};

bool bfs(){
    queue<node> q;q.push(node(Sx,Sy,0,0));
    while(!q.empty()){
        node p = q.front();q.pop();
        vis[p.x][p.y][p.exp] = true;
        if(p.x>=ans) continue;
        for(int i=0;i<4;i++){
            node now = p;
            now.x = p.x + xx[i] , now.y = p.y + yy[i],now.step++;
            if(now.x<0||now.x>=n||now.y<0||now.y>=m) continue;
            if(ditu[now.x][now.y]=='D') {ans = min(ans,now.step);continue;}
            if(ditu[now.x][now.y]=='X'&&!now.state[now.x][now.y]){
                if(now.exp==0) continue;
                else now.state[now.x][now.y] = true,now.exp--,now.step++;
            }
            if(ditu[now.x][now.y]>='0'&&ditu[now.x][now.y]<='9'&&!now.state[now.x][now.y]){
                now.state[now.x][now.y] = true;
                now.exp += ditu[now.x][now.y] - '0';
            }
            if(vis[now.x][now.y][now.exp]) continue;
            q.push(now);
        }
    }
    if(ans==inf) return false;
    else {cout<<ans<<endl;return true;}
}

int main()
{
    while(cin>>n>>m&&n&&m){
        init();
        if(!bfs()) puts("-1");
    }
    return 0;
}

View Code

后面想验证一下，到底是不是炸弹并步走，才导致的wrong，我就尝试将炸弹和入墙分为两步，再不同层进行。结果也AC。所以之前wrong就是BFS跨步走问题。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <map>

using namespace std;

const int inf = 2e9;

int n,m;
int Sx,Sy;

char ditu[9][9];
bool vis[9][9][600];

int xx[] = {1,-1,0,0};
int yy[] = {0,0,1,-1};

void init(){
    memset(vis,false,sizeof vis);
    for(int i=0;i<n;i++)for(int j=0;j<m;j++){
        char ch = getchar();while(ch==' '||ch=='\n') ch = getchar();
        ditu[i][j] = ch;
        if(ch=='S') Sx = i,Sy = j;
    }
}

struct node{
    int x,y,step,exp;
    int state[9][9];
    node(int a,int b,int c,int d):x(a),y(b),step(c),exp(d) {
        memset(state,0,sizeof state);
    };
};

bool bfs(){
    queue<node> q;q.push(node(Sx,Sy,0,0));vis[Sx][Sy][0] = true;
    while(!q.empty()){
        node p = q.front();q.pop();
        if(ditu[p.x][p.y]=='X'&&p.state[p.x][p.y]==2){
            p.state[p.x][p.y]=1;
            p.step++;
            q.push(p);
            continue;
        }
        for(int i=0;i<4;i++){
            node now = p;
            now.x = p.x + xx[i] , now.y = p.y + yy[i],now.step++;
            if(now.x<0||now.x>=n||now.y<0||now.y>=m) continue;
            if(ditu[now.x][now.y]=='D') {cout<<now.step<<endl;return true;}
            if(ditu[now.x][now.y]=='X'&&now.state[now.x][now.y]==0){
                if(now.exp==0) continue;
                else {
                    now.state[now.x][now.y] = 2,now.exp--;
                    if(vis[now.x][now.y][now.exp]) continue;
                    vis[now.x][now.y][now.exp] = true;
                    q.push(now);continue;
                }
            }
            if(ditu[now.x][now.y]>='0'&&ditu[now.x][now.y]<='9'&&!now.state[now.x][now.y]){
                now.state[now.x][now.y] = 1;
                now.exp += ditu[now.x][now.y] - '0';
            }
            if(vis[now.x][now.y][now.exp]) continue;
            vis[now.x][now.y][now.exp] = true;
            q.push(now);
        }
    }
    return false;
}

int main()
{
    while(cin>>n>>m&&n&&m){
        init();
        if(!bfs()) puts("-1");
    }
    return 0;
}

View Code

IDEA*

这里我DFS模拟，我决策函数用哈夫曼函数。然后模拟与上面BFS无疑，重点这里DFS也需要一步步来,因为想求得即最优。

可能存在没有答案，所以limit需要上限，8*8 = 64，64-2 = 62；然后取7个空作9炸弹，剩下55个空都是墙，然而63>55,所以55个墙为最坏情况，63+55 = 108步。上限为108；

（这里最坏情况假设，每次拿最近的炸弹必须用完之前的，每细想其他细节，所以大概就估算）

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <map>
#include <cmath>

using namespace std;

const int inf = 2e9;

int n,m;
int Sx,Sy,Fx,Fy;
int limit,nextd;

char ditu[9][9];
bool vis[9][9][600];
int state[9][9];

int xx[] = {1,-1,0,0};
int yy[] = {0,0,1,-1};

void init(){
    memset(vis,false,sizeof vis);
    memset(state,0,sizeof state);
    for(int i=0;i<n;i++)for(int j=0;j<m;j++){
        char ch = getchar();while(ch==' '||ch=='\n') ch = getchar();
        ditu[i][j] = ch;
        if(ch=='S') Sx = i,Sy = j;if(ch=='D') Fx = i,Fy = j;
    }
}

int check(int x,int y){
    return abs(x-Fx) + abs(y-Fy);
}

bool dfs(int x,int y,int step,int exp,int limit){
    int h = check(x,y);
    if(h+step>limit){
        nextd = min(h+step,nextd);
        return false;
    }
    if(h==0) {cout<<step<<endl;return true;}
    if(ditu[x][y]=='X'&&state[x][y]==2){
        state[x][y] = 1;
        if(dfs(x,y,step+1,exp,limit)) return true;
        return false;
    }
    for(int i=0;i<4;i++){
        int a = x + xx[i],b = y + yy[i],c = step+1,d = exp;
        if(a<0||a>=n||b<0||b>=m) continue;
        int flag = 0;
        if(ditu[a][b]=='X'&&!state[a][b]){
            if(d==0) continue;
            else{
                d--,state[a][b] = 2,flag = 1;
                if(vis[a][b][d]) continue;
                vis[a][b][d] = true;
                if(dfs(a,b,c,d,limit)) return true;
                vis[a][b][d] = false;
                if(flag) state[a][b] = 0;
                continue;
            }
        }
        if(ditu[a][b]>='0'&&ditu[a][b]<='9'&&!state[a][b]) state[a][b] = 1,flag = 1,d += ditu[a][b] - '0';
        if(vis[a][b][d]) continue;
        vis[a][b][d] = true;
        if(dfs(a,b,c,d,limit)) return true;
        vis[a][b][d] = false;
        if(flag) state[a][b] = 0;
    }
    return false;
}

int main()
{
    while(cin>>n>>m&&n&&m){
        init();
        int flag = 0;vis[Sx][Sy][0] = true;
        for(limit = check(Sx,Sy);limit<=102;){
            nextd = inf;
            if(dfs(Sx,Sy,0,0,limit)) {flag = 1;break;}
            limit = nextd;
        }if(flag) continue;
        puts("-1");
    }
    return 0;
}

View Code

Ali and BabaHDU - 4101

算法：BFS + 博弈判奇偶

难点：题目在于理解。因为博弈，两人都是以自己最优的思路操作。所以胜负关键点很重要。

胜负关键点在于，谁最后打开宝藏包围圈谁输。

题意：一副地图，只有一个宝藏，然后存在石头推（以数字表示，<100），然后每人每步可以打碎一个石头。然后走路不算操作数。

思路：第一步：先标记从宝藏出发能达到的0点（包括宝藏自身也要标记），因为到达这里就表示已经赢了；这里如果标记点，存在于边界，就表示Ali不用破碎石头就能拿宝藏，所以Ali Win；

　　　第二步：获取走到胜负关键点的总操作数。（胜负关键点就是谁可以走到那些上一步的标记点，因为谁都不想帮别人破最后的石头，所以就会选择破其他无关石头，所以要记录所有外围石头数即总操作数）；这里简单联想一下，就是这一步宝藏外围一定有一个石头包围圈即屏障，谁先打破谁输。

　　　第三步：第二步的重点在于记录石头数量，因为最后屏障是一个石头数量1的包围圈，这个包围圈石头数不用记录；然后所有外围石头数量总和判奇偶，奇数表示Baba要去破壁，所以Ali Win；反之同义。

失误：这里我wrong了；有两点：1）Baba Win 我写成了BaBa Win;2)第二步，我只用了（0，0）入队判断，其实不行，因为包围圈可能已经覆盖到边界了。所以要所有边界点入队判断；

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <map>
#include <cmath>

using namespace std;

int n,m,Sx,Sy,ans;

int ditu[303][303];
bool vis[303][303],vis2[303][303];
int xx[] = {1,-1,0,0};
int yy[] = {0,0,1,-1};

void init(){
    memset(vis,false,sizeof vis);
    memset(vis2,false,sizeof vis2);
    ans = 0;
}

struct node{
    int x,y;
    node(int a,int b):x(a),y(b) {};
};

bool bfs(){
    queue<node> q;
    q.push(node(Sx,Sy));vis2[Sx][Sy] = true;
    while(!q.empty()){
        node p = q.front();q.pop();
        if(p.x==0||p.x==n-1||p.y==0||p.y==m-1) return true;
        for(int i=0;i<4;i++){
            int x = p.x + xx[i],y = p.y + yy[i];
            if(x<0||x>=n||y<0||y>=m||ditu[x][y]!=0||vis2[x][y]) continue;
            q.push(node(x,y));
            vis2[x][y] = true;
        }
    }
    return false;
}

bool check(int x,int y){
    for(int i=0;i<4;i++) if(vis2[x+xx[i]][y+yy[i]]) return true;
    return false;
}

void bfs2(){
    queue<node> q;

    for(int j=0;j<m;j++){
        if(!vis[0][j]) q.push(node(0,j)),vis[0][j] = true,ans += ditu[0][j];
        if(!vis[n-1][j]) q.push(node(n-1,j)),vis[n-1][j] = true,ans += ditu[n-1][j];
    }
    for(int i=0;i<n;i++){
        if(!vis[i][0]) q.push(node(i,0)),vis[i][0] = true,ans += ditu[i][0];
        if(!vis[i][m-1]) q.push(node(i,m-1)),vis[i][m-1] = true,ans += ditu[i][m-1];
    }

    while(!q.empty()){
        node p = q.front();q.pop();
        if(check(p.x,p.y)) {ans --;continue;}
        for(int i=0;i<4;i++){
            int x = p.x + xx[i],y = p.y + yy[i];
            if(x<0||x>=n||y<0||y>=m||vis[x][y]) continue;
            q.push(node(x,y));
            vis[x][y] = true,ans+=ditu[x][y];
        }
    }
    //cout<<ans<<endl;
    if(ans%2) puts("Ali Win");
    else puts("Baba Win");
}

void show(){
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++) cout<<vis2[i][j]<<" ";cout<<endl;
    }
}

int main()
{
    while(~scanf("%d%d",&n,&m)){
        init();
        for(int i=0;i<n;i++) for(int j=0;j<m;j++){
            scanf("%d",&ditu[i][j]);
            if(ditu[i][j]==-1) Sx = i,Sy = j;
        }
        if(bfs()){
            puts("Ali Win");
        }else bfs2();
        //show();
    }
    return 0;
}

View Code

Ancient Messages HDU - 3839

算法：BFS

题意：就是给你一副图，图里面有很多埃及象形字，然后图像由像素0，1构成，1表示颜色黑，0则表示白。

难点：第一点在于怎么巧妙区别埃及象形字？每个埃及象形字都是有闭合空间并且数量对于每个埃及象形字不同，所以可以从空白入手。

　　　第二点在于如何区分埃及象形字内的空白与外空白？这里题目给出了关键点，就是每两个埃及象形字必不连接且不嵌套。并且黑色部分永远相连不断。

思路：预处理：这里使用十六进制代表二进制像素，所以需要还原。

　　　第一步：从边界开始读空白，进行白色BFS，把所有埃及象形字的外空白标记。

　　　第二步：从上到下从左到右，找埃及象形字，遇到则开始黑色BFS，每遇到白色没标记则开始白色BFS标记；重点记录，遇到几次空白，即这个埃及象形字有多少闭合空白空间。从而区分这个是什么埃及象形字；

　　第三步：通过BFS得出的埃及象形字数量，然后字典输出即可AC。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#include <map>
#include <cmath>

using namespace std;

int n,m,ditu[202][202],ans[8],cas=1;

int gg[] = {1,5,3,2,4,0};
char gk[] = {'A','D','J','K','S','W'};

int xx[] = {1,-1,0,0};
int yy[] = {0,0,1,-1};

bool vis[202][202];

struct node{
    int x,y;
    node(int a,int b):x(a),y(b) {};
};

void bfs_white(int a,int b){
    queue<node> q;
    q.push(node(a,b)),vis[a][b] = true;
    while(!q.empty()){
        node p = q.front();q.pop();
        for(int i=0;i<4;i++){
            int x = p.x + xx[i],y = p.y + yy[i];
            if(x<0||x>=n||y<0||y>=m||ditu[x][y]||vis[x][y]) continue;
            q.push(node(x,y)),vis[x][y] = true;
        }
    }
    return ;
}

void bfs_black(int a,int b){
    queue<node> q;
    int acer = 0;
    q.push(node(a,b)),vis[a][b] = true;
    while(!q.empty()){
        node p = q.front();q.pop();
        for(int i=0;i<4;i++){
            int x = p.x + xx[i],y = p.y + yy[i];
            if(x<0||x>=n||y<0||y>=m||vis[x][y]) continue;
            if(ditu[x][y]) q.push(node(x,y)),vis[x][y] = true;
            else bfs_white(x,y),acer++;
        }
    }
    ans[acer]++;
    return ;
}

void show(){
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++) cout<<ditu[i][j]<<" ";cout<<endl;
    }
}

int main()
{
    while(~scanf("%d%d",&n,&m)){
        if(!n&&!m) break;
        for(int i=0;i<n;i++) for(int j=0,z=0;j<m;j++){
            char ch = getchar();
            while(ch==' '||ch=='\n') ch = getchar();
            int num;
            if(ch>='a'&&ch<='z') num = ch-'a'+10;
            else num = ch-'0';
            if(num>=8) ditu[i][z++] = 1,num-=8;
            else ditu[i][z++] = 0;
            if(num>=4) ditu[i][z++] = 1,num-=4;
            else ditu[i][z++] = 0;
            if(num>=2) ditu[i][z++] = 1,num-=2;
            else ditu[i][z++] = 0;
            if(num>=1) ditu[i][z++] = 1;
            else ditu[i][z++] = 0;
        }m*=4;
        //show();

        memset(ans,0,sizeof ans);
        memset(vis,false,sizeof vis);

        //边界找0
        for(int j=0;j<m;j++){
            if(!vis[0][j]&&ditu[0][j]==0) bfs_white(0,j);
            if(!vis[n-1][j]&&ditu[n-1][j]==0) bfs_white(n-1,j);
        }
        for(int i=0;i<n;i++){
            if(!vis[i][0]&&ditu[i][0]==0) bfs_white(i,0);
            if(!vis[i][m-1]&&ditu[i][m-1]==0) bfs_white(i,m-1);
        }

        //找图像
        for(int i=0;i<n;i++)for(int j=0;j<m;j++) if(!vis[i][j]&&ditu[i][j]) bfs_black(i,j);

        printf("Case %d: ",cas++);
        for(int i=0;i<6;i++) for(int j=0;j<ans[gg[i]];j++) printf("%c",gk[i]);
        puts("");
    }
    return 0;
}

View Code

Booksort HDU - 1685

算法：IDA* /dfs

题意：给你一个打乱顺序的序列，每次操作可以选择一个长度的子连续序列插入任意位置，问最少需要多少次操作变成升序序列。

　　条件就是序列的数字一定连续的数字，即 1，2，3，4，5这样的数字。然后错过4次操作的答案，一律为5 or more

　　举例：5 4 3 2 1 ------> 3 2 5 4 1 -------> 3 4 1 2 5 ------------> 1 2 3 4 5 只要3步。

思路一：题意明确只要4步以内就行了。那就使用 IDA*的dfs进行limit+1慢慢推进，直到得出答案。

　　　难点：启发函数的设定。

　　　解决：序列分块，连续的为一块，即1 4 2 3 5 序列分成 4块 1、 4 、 23、 5；

　　　　　　这里注意， 如果第一块为1，其本身不应该算进去，因为至始至终都不会移动这一块；最末端块同理；因为 1 和 5 本身就在其最终位置上永远不需要动，

　　　　　　所以只要改变 4，23两块就行了，即需要操作的块数为2。

　　　　 然后每次操作都会影响3块的后缀块变化，即分离块的前一块的、分离块本身与被插入点前面那块这3块的后缀；理想情况下，每次改变都使得其连接成一块，即每次操作减少3块。

　　　　　　所以1 4 2 3 5 序列启发函数 h(x) = ceil(操作块数/3)，向下取整，即是1。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>

using namespace std;

const int INF = 2e9;

int n,num[20];

void init(){
    cin>>n;
    for(int i=1;i<=n;i++) cin>>num[i];
    num[0]=0;num[n+1]=n+1;
}

void show(){
    for(int i=1;i<n+1;i++){
        cout<<num[i]<<" ";
    }cout<<endl;
}

int forLimit(){
    double ans = 0;
    for(int i=0;i<=n;i++) if(num[i]+1!=num[i+1]) ans++;
    return ceil(ans/3);
}

bool dfs(int step,int limit){
    int h = forLimit();
    if(h+step>limit) return false;
    if(h==0){
        cout<<step<<endl;
        //show();
        return true;
    }
    int temp[20];
    memcpy(temp,num,sizeof(num));
    for(int i=1;i<=n;i++) for(int len=1;len<=n-i+1;len++) for(int pos=1;pos<=n-len+1;pos++) if(pos!=i){
        for(int j=0;j<len;j++) num[pos+j] = temp[i+j];
        for(int p=1,j=1;j<=n;){
            if(j<pos) num[j++] = temp[p++];
            else if(j==pos) j+=len;
            else if(p==i) p+=len;
            else num[j++] = temp[p++];
        }
        if(dfs(step+1,limit)) {
                //memcpy(num,temp,sizeof(temp));show();
                return true;
        }
    }
    memcpy(num,temp,sizeof(temp));
    return false;
}

int main()
{
    int _;cin>>_;
    while(_--){
        init();
        for(int limit=forLimit();;limit++){
            if(limit>4) {puts("5 or more");break;}
            if(dfs(0,limit)) break;
        }
    }
}

View Code

思路二：观看大神博客https://blog.csdn.net/ilsswfr/article/details/52012467

　　　　类似于双向遍历bfs一样。

　　　　第一步：从初始序列开始dfs两步，得出答案为解。用set记录所有得出的序列。

　　　　第二部：从目标序列开始dfs两步，如果出现的序列在set里面则步数+2为解。

//从初始情况搜索两层并记录每次状态，这两层中如果有解，直接输出
//若是无解，从有序状态往回搜一层和两层，
//如果能达到与之前的相同的状态就是有解。
 
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cctype>
#include<cstdio>
#include<string>
#include<cstring>
#include<vector>
#include<set>
#include<map>
#include<queue>
#include<cmath>
#define pi acos(-1.0)
#define inf 1<<29
#define INF 0x3f3f3f3f
#define zero 1e-8
 
using namespace std;
int step, n;
int arr[100];
 
int fin[100];
 
set<string> ff;
 
int makenum(int num, char *s, int &k)
{
 
    int i = 0, now[5] = {};
    for (; num;) {
        now[++i] = num % 10;
        num /= 10;
    }
    for (int j = i; j; j--) {
        s[k++] = now[j] + '0';
    }
    return k;
 
}
 
string makestr(int *s, int num)  //样式
{
 
    string aa;
    char a[100];
    int k = 0;
    for (int i = 0; i < num; ++i) {
        makenum(s[i], a, k);
        a[k++] = ' ';
    }
    a[k] = '\0';
    return a;
 
}
bool compare(int *s)
{
    for (int i = 0; i < n; ++i)
        if (fin[i] != s[i]) return false;
 
    return true;
}
void show(int *s)
{
    for (int i = 0; i < n; ++i)
        cout << s[i];
    cout << endl;
}
void cop(int *en, int *be)
{
    for (int i = 0; i < n; ++i)
        en[i] = be[i];
}
void dfs1(int *tem, int cnt, int now)
{
    string str = makestr(tem, n);
    ff.insert(str);
    if (step != inf) return ;
    if (cnt == now) {
        if (compare(tem)) {
            step = cnt;
        }
 
        return ;
    }
 
    if (cnt < now) return ;
    int tt[100];
 
    for (int j = 0; j < n; ++j) {
 
        int z;
        for (z = 0; z < j; ++z)
            tt[z] = tem[z];
        for (int len = 1; len < n - j; ++len) {
            cop(tt, tem);
 
            int f = z + len;
            for (int sert = 0; sert < n - j - len; ++sert) {
                tt[z + sert] = tem[f + sert];
 
                if (f + sert + 1 < n - j - len
                        && tem[f + sert + 1] == tt[z + sert] + 1) continue;
 
                for (int kk = 1; kk <= len; ++kk)
                    tt[z + sert + kk] = tem[j + kk - 1];
 
                string str = makestr(tt, n);
                ff.insert(str);
                dfs1(tt, cnt, now + 1);
            }
 
        }
    }
}
 
void dfs2(int *tem, int cnt, int now)
{
 
    if (step != inf) return ;
    string str = makestr(tem, n);
    if (cnt == now) {
        if (ff.find(str) != ff.end())
            step = 0;
        return ;
    }
 
    int tt[100];
 
    for (int j = 0; j < n; ++j) {
 
        int z;
        for (z = 0; z < j; ++z)
            tt[z] = tem[z];
        for (int len = 1; len < n - j; ++len) {
            cop(tt, tem);
 
            int f = z + len;
            for (int sert = 0; sert < n - j - len; ++sert) {
                tt[z + sert] = tem[f + sert];
 
                if (f + sert + 1 < n - j - len
                        && tem[f + sert + 1] == tt[z + sert] + 1) continue;
 
                for (int kk = 1; kk <= len; ++kk)
                    tt[z + sert + kk] = tem[j + kk - 1];
                dfs2(tt, cnt, now + 1);
            }
 
        }
    }
}
 
void makefin()
{
    for (int i = 0; i < n; ++i)
        fin[i] = i + 1;
}
 
int main()
{
    int t;
    cin >> t;
    for (; t--;) {
        scanf("%d", &n);
 
        for (int i = 0; i < n; ++i) {
            scanf("%d", &arr[i]);
        }
        makefin();
        step = inf;
 
        for (int i = 0; i <= 2; ++i) {
            step = inf;
            ff.clear();
            dfs1(arr, i, 0);
            if (step != inf) {
                printf("%d\n", step);
                break;
            }
        }
        if (step == inf) {
            for (int i = 1; i <= 2; ++i) {
 
                dfs2(fin, i, 0);
                if (step != inf) {
                    printf("%d\n", i + 2);
                    break;
                }
            }
            if (step == inf) printf("5 or more\n");
        }
    }
    return 0;
}

View Code

BeatHDU - 2614

算法：dfs

题意：给一个矩阵Tij，行为i，列为j，Tij数字为在做完第i题之后，会花费Tij时间去做第j题；这里题的难度与时间正相关。

　　　条件：1.acm大佬只做难度递增的题，即时间需要递增；

　　　　　　2.永远从第一题开始做起，而且花费时间永远为0

思路：就是从第一行开始往下dfs，需要每次都做更难或者相同难度的题。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>

using namespace std;

int T[20][20],n,ans;
bool ck[20];

void init(){
    memset(ck,false,sizeof ck);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++) cin>>T[i][j];
    ans=1;
}

//x:上一题  y:上一题花费时间 z:总做题数
void dfs(int x,int y,int z){
    if(ans==n) return;
    if(z==n){ans = n;return ;}
    int flag = 1;
    for(int j=2;j<=n;j++) if(!ck[j]&&T[x][j]>=y){
        flag = 0;
        ck[j]=true;
        dfs(j,T[x][j],z+1);
        ck[j]=false;
    }
    if(flag) ans = max(ans,z);
    return ;
}

int main()
{
    while(cin>>n){
        init();
        ck[1] = true;
        dfs(1,0,1);
        cout<<ans<<endl;
    }
}

View Code

Roll The CubeHDU - 3309

算法：bfs

题意：给一个外边界都是墙的地图，然后里边也有墙，即障碍物；给你两个球，可以上下左右滚动一格，然后每次操作都是同步，撞墙就不能动，两个球不能重叠。地图必有两个洞，目标就是算将两个球滚进洞里　　　　的最短操作数。

思路/难点：简单的模拟题，用BFS。

　　　　　第一：BFS需要记录每一操作状态；状态有：球1坐标、球2坐标、球1进洞状态、球2进洞状态、洞1状态、洞2状态、步数。

　　　　　　　　需要维护球进洞状态：因为如果球进洞了的话，不管这么滚，坐标都不动，并且，当一个球进洞了，那么两个球是可以重叠到一个坐标上。

　　　　　　　　需要维护洞状态：判断球是否能进此洞。

　　　　　第二：排重：需要状态数组进行避免重复操作。这里因为两个球，所以就用四维数组，即球1坐标、球2坐标进行排重。不管球是否进洞都可以判断；

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

int n,m;
bool mp[24][24];
bool ck[24][24][24][24];
int bx[3],by[3];
int hx[3],hy[3];
int xx[]={0,0,1,-1};
int yy[]={1,-1,0,0};

void init(){
    memset(mp,true,sizeof mp);
    memset(ck,true,sizeof ck);
    cin>>n>>m;
    int bNum=0,hNum=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            char ch = getchar();
            while(ch=='\n'||ch==' ') ch=getchar();
            if(ch=='*') mp[i][j]=false;
            else if(ch=='B') bx[bNum]=i,by[bNum++]=j;
            else if(ch=='H') hx[hNum]=i,hy[hNum++]=j;
    }
}

void show(){
    cout<<n<<" "<<m<<endl;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++) cout<<mp[i][j]<<" ";cout<<endl;
    }cout<<endl;
    cout<<bx[0]<<" "<<by[0]<<" "<<bx[1]<<" "<<by[1]<<endl;
    cout<<hx[0]<<" "<<hy[0]<<" "<<hx[1]<<" "<<hy[1]<<endl;
    cout<<endl;
}

struct node{
    int x1,y1,x2,y2,bS1,bS2,hS1,hS2,step;
    node(int xx1,int yy1,int xx2,int yy2,int bbS1,int bbS2,int hhS1,int hhS2,int stepp)
    :x1(xx1),y1(yy1),x2(xx2),y2(yy2),bS1(bbS1),bS2(bbS2),hS1(hhS1),hS2(hhS2),step(stepp) {};
};

void change(int &x,int &y,int bS,int i){
    if(bS==1) return ;
    if(mp[x+xx[i]][y+yy[i]]) x += xx[i] , y += yy[i];
    return;
}

int check(int x,int y,int &hS1,int &hS2){
    if(hS1==0&&x==hx[0]&&y==hy[0]) {hS1=1;return 1;}
    if(hS2==0&&x==hx[1]&&y==hy[1]) {hS2=1;return 1;}
    return 0;
}

int bfs(){
    queue<node> q;
    q.push(node(bx[0],by[0],bx[1],by[1],0,0,0,0,0));ck[bx[0]][by[0]][bx[1]][by[1]] = false;
    while(!q.empty()){
        node p = q.front();q.pop();
        for(int i=0;i<4;i++){
            int x1=p.x1,y1=p.y1,x2=p.x2,y2=p.y2,bS1=p.bS1,bS2=p.bS2,hS1=p.hS1,hS2=p.hS2;
            change(x1,y1,bS1,i);change(x2,y2,bS2,i);
            if(bS1==0&&bS2==0&&x1==x2&&y1==y2) continue;
            if(ck[x1][y1][x2][y2]==false) continue;
            ck[x1][y1][x2][y2]=false;
            if(bS1==0) bS1 = check(x1,y1,hS1,hS2);
            if(bS2==0) bS2 = check(x2,y2,hS1,hS2);
            if(hS1&&hS2) return p.step+1;
            q.push(node(x1,y1,x2,y2,bS1,bS2,hS1,hS2,p.step+1));
        }
    }
    return -1;
}

int main()
{
    int _;cin>>_;
    while(_--){
        init();//show();
        int ans = bfs();
        if(ans==-1) puts("Sorry , sir , my poor program fails to get an answer.");
        else cout<<ans<<endl;
    }
}

View Code

JerboasHDU - 2437

算法：优先队列+BFS

题意：就是一个老鼠，他有很多个洞，TP，临时和永久两种；给你一个洞与洞的单向路径图，而且没有自身到自身的路径；给出数字K，问从S洞开始，到任意一个永久洞的最短路，并且路径长度必须为K的倍数。

思路：这里求最短路径，立马就想到BFS。

　　　1.因为洞S题目已经给出了，初始洞一定为临时洞。

2.这里没有明确表示两个洞之间只有唯一路径，所以需要考虑两个洞存在不同长度的路径，使用二维vector存储。

3.判重关键点，路径长度和K倍数，所以只要求路径长度对K求余的余数就能判断，K最大为1000 所以判重数组，二维只要开到1000左右，即vis[点数量][1001]。

4.这里因为并不是简单判断最短路径，并且需要K倍数，对路径排序并没有用，所以需要优先队列，对入队的最短路进行优先出队。

我的出错点：这里我受到之前做题的影响，因为我上一道题的bfs是步骤，每次只加一，所以把判断放在了入队前也没问题。然而对于现在这题来说不行。所以需要入队完，从队列取出来再判断，再加上是优先队列，每次取出来都是最短路，只要达到要求就是答案。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>
#include <set>

using namespace std;

int n,m,s,k;
char dong[1002];

struct guan{
    int e,f;
    guan(int ee,int ff):e(ee),f(ff) {};
};
vector<guan> v[1002];

bool vis[1002][1001];

void init(){
    cin>>n>>m>>s>>k;
    for(int i=1;i<=n;i++){
        char ch = getchar();while(ch=='\n' || ch==' ') ch = getchar();
        dong[i] = ch;
    }
    for(int i=1;i<=n;i++) v[i].clear();
    memset(vis,false,sizeof vis);
    for(int i=0;i<m;i++){
        int a,b,c;cin>>a>>b>>c;
        v[a].push_back(guan(b,c));
    }
}

struct node{
    int x,y;
    node(int xx,int yy):x(xx),y(yy) {};
    bool operator < (const node &a) const{
        if(y==a.y ) return x>a.x;
        return y>a.y;
    }
};

bool bfs(){
    priority_queue<node> q;
    vis[s][0] = true;q.push(node(s,0));
    while(!q.empty()){
        node p = q.top();q.pop();
        int x = p.x , y = p.y;
        if(dong[x]=='P'&&y%k==0){
                cout<<y<<" "<<x<<endl;
                return true;
            }
        for(int i=0;i<v[x].size();i++){
            int e = v[x][i].e , f = v[x][i].f + y;
            if(vis[e][f%k]) continue;
            vis[e][f%k] = true;
            q.push(node(e,f));
        }
    }
    return false;
}

int main()
{
    int _;cin>>_;
    for(int i=1;i<=_;i++){
        init();
        cout<<"Case "<<i<<": ";
        if(!bfs()) cout<<"-1 -1"<<endl;
    }
}

View Code

Open the LockHDU - 1195

算法：BFS

题意：给一个4位数，然后对位数上面的数进行操作，可以加一减一，9+1 = 1，1-1=9；可以与相邻的位数互换。

思路：简单的模拟题。因为这里只给了四位数，判重方法直接用vis[10][10][10][10]记录4个位数变化就好了

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>
#include <set>

using namespace std;

int n[5],e[5];
bool vis[10][10][10][10];

void init(){
    memset(vis,true,sizeof vis);
    int num;cin>>num;
    for(int i=3;i>=0;i--){
        n[i] = num%10;
        num/=10;
    }
    cin>>num;
    for(int i=3;i>=0;i--){
        e[i] = num%10;
        num/=10;
    }
}

struct node{
    int t[5],step;
    node(int *a,int sstep){
        for(int i=0;i<4;i++) t[i] = a[i];
        step = sstep;
    }
    bool check(){
        if(vis[t[0]][t[1]][t[2]][t[3]]) {
            vis[t[0]][t[1]][t[2]][t[3]] = false;
            return true;
        }
        return false;
    }
    void left(int i){
        int a = t[i];
        t[i] = t[i-1];
        t[i-1] = a;
    }
    void right(int i){
        int a = t[i];
        t[i] = t[i+1];
        t[i+1] = a;
    }
    bool ansCheck(){
        for(int i=0;i<4;i++) if(t[i]!=e[i]) return false;
        return true;
    }
};

int bfs(){
    queue<node> q;
    q.push(node(n,0));
    vis[n[0]][n[1]][n[2]][n[3]] = false;

    while(!q.empty()){
        node p = q.front();q.pop();

        if(p.ansCheck()) return p.step;

        for(int i=0;i<4;i++){
            //==============================
            node temp = p;temp.step++;
            if(temp.t[i]==9) temp.t[i] = 1;
            else temp.t[i]++;
            if(temp.check()) q.push(temp);
            //==============================
            temp = p;temp.step++;
            if(temp.t[i]==1) temp.t[i] = 9;
            else temp.t[i]--;
            if(temp.check()) q.push(temp);
            //==============================
            temp = p;temp.step++;
            if(i!=0){
                temp.left(i);
                if(temp.check()) q.push(temp);
            }
            //==============================
            temp = p;temp.step++;
            if(i!=3){
                temp.right(i);
                if(temp.check()) q.push(temp);
            }
        }
    }

    return -1;
}

void show(){
    for(int i=0;i<4;i++) cout<<n[i]<<" ";cout<<endl;
    for(int i=0;i<4;i++) cout<<e[i]<<" ";cout<<endl;
}

int main()
{
    int _;cin>>_;
    while(_--){
        init();//show();
        cout<<bfs()<<endl;
    }
}

View Code

Pushing Boxes POJ - 1475

算法：BFS

题意：推箱子游戏，游戏规则：人只能有两个操作，一个就是走，另一个就是推箱子。目标就是把箱子推到目标位置。然后求推操作数量最小为前提的最短路径。

思路1：这个是我想的，直接用优先队列，每个点记录，人位置、箱子位置、推的数量、步数；然后优先推数量最小在前面，然后相同则步数最小。

　　 排重这里我用 [ 人X坐标 ] [ 人Y坐标 ] [ 箱子X坐标 ] [ 箱子Y坐标 ] [ 推数量 ] 五维数组维护，然后TL了。后面把推数量去掉，就ac了。

　　（这里想了一下，优先队列已经维护了推数量最少，排重数组不需要维护，因为之前出现过推数量，在人与箱子相对位置的情况下，必为最优；即先存在为最优）

　　　然后唯一注意的点是，这里输出答案两个之间有一个空行。没留意，wrong了很多次。看了人家代码才发现。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int INF = 2e9;

int n,m;
int Sx,Sy,Bx,By,Tx,Ty;
bool mp[21][21];
bool vis[21][21][21][21];
int xx[] = {0,0,-1,1};
int yy[] = {1,-1,0,0};
char fch[] = {'e','w','n','s'};
char bch[] = {'E','W','N','S'};

bool checkXY(int a,int b){
    if(a<=0||b<=0||a>n||b>m) return false;
    return mp[a][b];
}

struct node{
    int a,b,c,d,step,p;
    string ans;
    node(int aa,int bb,int cc,int dd,string ss,int sstep,int pp):a(aa),b(bb),c(cc),d(dd),ans(ss),step(sstep),p(pp) {};
    bool check(){
        if(c==Tx&&d==Ty) return true;
        return false;
    }
    bool operator < (const node &x) const{
        if(p==x.p) return step>x.step;
        return p>x.p;
    }
};

void init(){
    memset(mp,true,sizeof mp);
    memset(vis,true,sizeof vis);
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++){
        char ch=getchar();while(ch=='\n') ch=getchar();
        if(ch=='#') mp[i][j] = false;
        else if(ch=='S') Sx=i,Sy=j;
        else if(ch=='B') Bx=i,By=j;
        else if(ch=='T') Tx=i,Ty=j;
    }
}

void show(){
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++) cout<<mp[i][j]<<" ";cout<<endl;
    }
}

bool bfs(){
    priority_queue<node> q;
    q.push(node(Sx,Sy,Bx,By,"",0, 0));
    vis[Sx][Sy][Bx][By] = false;
    while(!q.empty()){
        node p = q.top();q.pop();
        if(p.check()){
            cout<<p.ans<<endl;
            return true;
        }
        for(int i=0;i<4;i++){
            node u = p;u.a += xx[i],u.b += yy[i];
            if(!checkXY(u.a,u.b)) continue;
            bool flag = false;
            if(u.a==u.c&&u.b==u.d) flag = true;
            if(flag){
                u.c += xx[i],u.d += yy[i];
                if(!checkXY(u.c,u.d)) continue;
                if(!vis[u.a][u.b][u.c][u.d]) continue;
                vis[u.a][u.b][u.c][u.d] = false;
                u.ans+=bch[i];
                u.step++;
                u.p++;
                q.push(u);
            }else{
                if(!vis[u.a][u.b][u.c][u.d]) continue;
                 vis[u.a][u.b][u.c][u.d] = false;
                 u.ans+=fch[i];
                 u.step++;
                 q.push(u);
            }
        }
    }
    return false;
}

int main()
{
    int cas = 1;
    while(cin>>n>>m&&n&&m){
        cout<<"Maze #"<<cas++<<endl;
        init();
        if(!bfs()) puts("Impossible.");
        cout<<endl;
    }
}

View Code

思路2：这个是看别人博客学的。http://t.zoukankan.com/xiaoguapi-p-10389623.html

　　　　大意就是进行一次箱子到目标位置的BFS求最短路径，然后在箱子BFS内部嵌套一个人推箱子的BFS求人到箱子位置的最短路径。

　　　重点：1.箱子每一步，都要去BFS判断人能不能走到箱子上一步位置，不行则箱子走不了。2.判重，外围bfs只需要维护箱子位置就行，内部每一次BFS判重也只维护人的位置即可。

代码详情看大神博客。

2022年的第一道题，虎年好!

Full Tank?POJ - 3635

算法：优先队列bfs

题意：给一张地图，上面有N个城市，M条双向非负权值道路，每条路的权值是油耗，即过这条路需要多少油量。然后每个城市油价不同。

　　　然后给你一辆油箱容量为C的车，问你从城市S到城市E的一条花费最少油费的路。

思路：第一次：这里我一开始，通过测试数据发现，最短路径不是最优路径，因为你要考虑每个城市油价进行加油的最优策略，即需要每次都需要找路径进行总油价比较，就使用了dfs，然后TLE。

　　　第二次：吸取教训，想着试一下BFS，需要判重数组，思考影响答案的因素是，路径中城市的选择还有每个城市的加油量，然后就用二维数组vis[x][y]，x表示城市，y表示油量，vis数组表示在城市x时拥有　　　　y升油的money花费，通过几时加油来控制计算money，总money小过vis数组的进队列，否则不进队列。队列的点需要维护点前城市now和油量fuel和总花费钱数money。因为这里求最小花费，我就用优先队列，进行money的排序，到达目标城市即最优。然后还是TLE了。

　　　第三次：这个时候我看了别人大牛博客参考，https://www.cnblogs.com/SiriusRen/p/6532446.html。他和我思路不同的地方在于，我是直接两个循环嵌套，第一个循环找城市，第二个循环找加油量，通过已有状态向下推。他则是把加油和找城市去分开，而且他的加油是，一次只加一升。我一下子就意识到自己的错误了。

　　　重点：以往的判重都是bool，而这次是维护一个money最小，而且你是用优先队列维护了，城市转移会影响油价，潜在地影响money，所以每次城市转移都需要进行入队维护，同理，加油直接影响了money，每加一升都会影响，所以加油之后也要进入队列进行维护。保证每次取出的点状态都是最优，不然就会产生冗余。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int INF = 0x3f3f3f3f;

int n,m,c,s,e;
int price[1001],vis[1001][101];

struct Edge{
    int v,cost;
    Edge(int _v,int _cost):v(_v),cost(_cost) {}
};vector<Edge> E[1001];
void addedge(int u,int v,int w){
    E[u].push_back(Edge(v,w));
    E[v].push_back(Edge(u,w));
}

void init(){
    cin>>n>>m;
    for(int i=0;i<n;i++) cin>>price[i];
    for(int i=0;i<m;i++){
        int a,b,c;cin>>a>>b>>c;
        addedge(a,b,c);
    }
}

struct node{
    int now,fuel,money;
    node(int nn,int ff,int mm):now(nn),fuel(ff),money(mm) {}
    bool check(){
        if(now==e) return true;
        return false;
    }
    bool operator < (const node &x) const{
        if(money==x.money) return fuel<x.fuel;
        return money > x.money;
    }
};

bool bfs(){
    memset(vis,INF,sizeof vis);
    priority_queue<node> q;
    q.push(node(s,0,0));vis[s][0]=0;
    while(!q.empty()){
        node p = q.top();q.pop();
        if(p.check()){cout<<p.money<<endl;return true;}
        //-----加一升油---------------------------------
        if(p.fuel<c){
            int now = p.now , fuel = p.fuel, money = p.money;
            fuel++;money+=price[now];
            if(money<vis[now][fuel]){
                vis[now][fuel] = money;
                q.push(node(now,fuel,money));
            }
        }
        //-----去下个城市-----------------------------
        for(int i=0;i<E[p.now].size();i++){
            int now = p.now , fuel = p.fuel, money = p.money;
            if(E[now][i].cost>fuel) continue;
            int v = E[now][i].v,cost = E[now][i].cost;
            fuel -= cost;
            if(money<vis[v][fuel]){
                vis[v][fuel] = money;
                q.push(node(v,fuel,money));
            }
        }
    }
    return false;
}

int main()
{
    init();int _;cin>>_;
    while(_--){
        cin>>c>>s>>e;
        if(!bfs()) puts("impossible");
    }
}

View Code

　　大牛博客谈到：图上dp函数，F[i][j] = Min(F[i][j-L]+price[i]*L,F[k][j+dist(i,k)]) 。我们初学dp都是从左上开始往右下推，dp是从已经确定的状态往后推，而这个图上的dp给我感觉就是前面点状态不是最优，需要通过后面重新读图进行反复推敲。这里说到spfa，其实就是有同样感觉，我忘了差不多，等到后面刷最短路径的题再回来思考，这里spfa+dp为什么会TLE。

Weather ForecastPOJ - 2044

算法：BFS+判重减枝

题意：一个4*4的正方形地图上有16个城市，你是上帝，能控制一朵2*2正方形的云，云下面的城市一定是阴天下雨，其余一定是晴天。你可以控制云朵运动：1.留在原地，2.东南西北方向走一步 3.东南西北方向走两步；然后城市节假日不能有雨；一个城市最多只能6天不下雨。

思路：一开始，暴力bfs，TLE。然后加入判重数组减枝，重要因素就是，天数、云位置、城市干旱时间天数；由于干旱极限是7天，状态压缩7的16次方，开个三维数组，这个肯定MLE。然后思考，一朵云覆盖4个城市，刚好可以把地图分成9个重叠块，而四个角落城市，分别只有一个形式的云覆盖，因此这四个角落是最容易干旱的，如果出现错过7天的情况，最早出现的城市一定有这四个角落城市其中一个，所以干旱程度只要记录四个角落就行了，然后开个6维数组，vis【天数】【云朵位置】【西北角落】【东北角落】【西南角落】【东南角落】。

我的错误点：就是你要注意看题，我一开始理解为走两步，虽然已经说了不能走斜线，但是我想你走两步，第一步走北，第二步走东，合在一起不就是走了东北吗？其实不是的，只能同一方向走两步。

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int INF = 0x3f3f3f3f;

int N,W[367][18];
int C[10][5]={{1,2,5,6},{2,3,6,7},{3,4,7,8},{5,6,9,10},{6,7,10,11},{7,8,11,12},{9,10,13,14},{10,11,14,15},{11,12,15,16}};
int G[10][4]={{4,5,7,8},{3,5,6,8},{3,4,6,7},{1,2,7,8},{0,2,6,8},{0,1,6,7},{1,2,4,5},{0,2,3,5},{0,1,3,4}};
bool VIS[367][10][7][7][7][7];

bool check(int a,int b){
    for(int i=0;i<4;i++){
        if(W[b][C[a][i]]==1) return false;
    }
    return true;
}

bool dfs(int a,int b,int zero,int two,int six,int eight){
    if(b>N) return true;
    for(int i=0,j=0;i<9;i++){
        if(i==G[a][j]) {j++;continue;}
        if(!check(i,b)) continue;

        int zz=zero,tt=two,ss=six,ee=eight;
        zz++,tt++,ss++,ee++;
        if(i==0) zz=0;else if(i==2) tt=0;else if(i==6) ss=0;else if(i==8) ee=0;
        if(zz>6||tt>6||ss>6||ee>6) continue;

        if(VIS[b][i][zz][tt][ss][ee]) continue;
        VIS[b][i][zz][tt][ss][ee]=true;
        if(dfs(i,b+1,zz,tt,ss,ee)) return true;
    }
    return false;
}

void show(){
    for(int i=0;i<9;i++){
        for(int j=0;j<4;j++) cout<<C[i][j]<<" ";cout<<endl;
    }
    for(int i=0;i<9;i++){
        for(int j=0;j<4;j++) cout<<G[i][j]<<" ";cout<<endl;
    }
    for(int i=1;i<=N;i++){
        for(int j=1;j<=16;j++) cout<<W[i][j]<<" ";cout<<endl;
    }
}

int main()
{
    while(cin>>N&&N){
        memset(VIS,false,sizeof VIS);
        for(int i=1;i<=N;i++)for(int j=1;j<=16;j++) cin>>W[i][j];
        if(!check(4,1)) {cout<<0<<endl;continue;}
        VIS[1][4][1][1][1][1] = true;
        if(!dfs(4,2,1,1,1,1)) cout<<0<<endl;
        else cout<<1<<endl;
    }
    return 0;
}

View Code

Remmarguts' DatePOJ - 2449

题意：一个公主来外交，王子需要从他的车站走到公主的车站去接她，公主要求王子必须走第K短路线找她。地图是一个单向路径的有环图。其实就是经典K短路。

算法：SPFA+A* 这里简单解释一下啊 SPFA 可以求有环图的，并且能判断图是否有负环，最终可以求出从起点出发到地图所有点的最短路径

思路：第一步：先用SPFA反向从终点即公主，开始算出到所有其他车站的最短距离，用dist数组记录

　　　第二步：从王子开始A* BFS遍历，用优先队列维护与公主终点的距离。f(x) = h(x) + g(x). 这里构造启发函数就是与起点的距离 + dist数组来预估与公主的距离。然后开始出队找终点，找到第K个就是答案了。

　　第三步：剪枝，这题有没有都可以过。1） dist数组里是INF的点都可以直接跳过；2）用cnt数组记录每个点的入队数，第K短里面的点最多只可能入队K次超过可以跳过

难点/易错点：第一：优先队列特性是取点就进行判断答案以保证最优准确性。然后我是用cnt数组来判断，但是我犯了个错误，就是cnt数组剪枝的时候，放在了入队前。其实应该是出队后，因为要确保同一层的可能的答案点都进入队列，所以要放到下一层。

　　　　　　第二：就是特殊情况，当起点和终点都是同一个点的时候，K要+1。因为你起点，一开始入队并且出队的时候，记录数值会加一，但是王子根本没有走任何一条路，所以K要加一，让循环推到下一层。

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int INF = 0x3f3f3f3f;
const int MAXN = 1010;

int n,m,s,t,k;

struct Edge{
    int v;
    int cost;
    Edge(int _v=0,int _cost=0):v(_v),cost(_cost) {}
};
vector<Edge> E1[MAXN];
vector<Edge> E2[MAXN];

void addedge(int u,int v,int w){
    E1[u].push_back(Edge(v,w));
    E2[v].push_back(Edge(u,w));
}

bool vis[MAXN];
int cnt[MAXN],dist[MAXN];

bool SPFA(int start,int n){
    memset(vis,false,sizeof vis);
    for(int i=1;i<=n;i++) dist[i]=INF;
    vis[start]=true;dist[start]=0;
    queue<int> que;
    que.push(start);
    memset(cnt,0,sizeof cnt);cnt[start]++;
    while(!que.empty()){
        int u=que.front();que.pop();
        vis[u]=false;
        for(int i=0;i<E2[u].size();i++){
            int v = E2[u][i].v;
            if(dist[v]>dist[u]+E2[u][i].cost){
                dist[v]=dist[u]+E2[u][i].cost;
                if(vis[v]) continue;
                vis[v]=true;
                que.push(v);
                if(++cnt[v]>n) return false;
            }
        }
    }
    return true;
}

void init(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        addedge(a,b,c);
    }
   scanf("%d%d%d",&s,&t,&k);
   if(s==t) k++;
}

struct node{
    int cz,time,f;
    node(int _cz,int _time):cz(_cz),time(_time) {
        f = time + dist[cz];
    }
    bool operator < (const node &a) const{
        return f>a.f;
    }
};

int AStar(){
    priority_queue<node> q;
    memset(cnt,0,sizeof cnt);
    if(dist[s]==INF) return -1;
    q.push(node(s,0));
    while(!q.empty()){
        node p = q.top();q.pop();
        int u = p.cz;
        cnt[u]++;
        if(cnt[u]>k) continue;
        if(u==t&&cnt[u]==k) return p.time;
        for(int i=0;i<E1[u].size();i++){
            int v = E1[u][i].v;
            int cost = E1[u][i].cost;
            if(dist[v]==INF) continue;
            q.push(node(v,p.time+cost));
        }
    }
    return -1;
}

int main()
{
    init();SPFA(t,n);
    printf("%d\n",AStar());
    return 0;
}

View Code

Holedox MovingPOJ - 1324

题意：一个n,m的巢穴地图，里面有石头不能走，洞口永远为（1,1）。然后给你一条长度L[2,8]的蛇。然后蛇每一次移动，身体也会跟着走，然后你不能穿过石头和身体。问你到洞口的最短步数是多少？

算法：A*+状态压缩

思路：这里启发函数就直接蛇头与洞口曼哈顿距离就行了；

　　　判重函数：这里每个点维护的信息：蛇头坐标，步数，蛇身体状态；其实区分每一个点入队的判重，这里就重要是蛇头和身体状态（因为身体也会阻碍蛇头前进）；蛇头直接二维x,y就行了；然后就是蛇身体如何区分记录呢？一开始我的想法是，最大长度为8，那再记录身体其他坐标就好了，但是21的16次方直接爆了，MLE。然后想了很久，还是看了别人博客，学到了。只要记录蛇头，然后第二节只要记录方向就行，第三节只要记录相对于第二节的方向就行了，等等。因为方向只有4个方向，所以最大只要 4的7次方就是 2 的14次方；所以开三维，vis[21][21][1<<14]

难点/易错点：我直接1A了，没有什么地方出错；求方向四进制状态、还原身体坐标、维护新的四进制状态这几个可能会比较容易搞得混乱，我自己也码的不好看，但也懒得改了，希望能帮到你

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>

using namespace std;

const int INF = 0x3f3f3f3f;
const int MAXN = 1010;

int four[7];//四进制基数
int n,m;//迷宫长宽
int stNum;bool ditu[21][21];//石头数+地图标记
int snakeNum;//蛇的长度
int snakeHeadX,snakeHeadY,snakeBody;//蛇头坐标  + 蛇形状的四进制表示（用四进制记录每一节对于前一节的方向）
bool vis[21][21][1<<14];//蛇头坐标  + 蛇形状的四进制表示 de  三维标记判重函数
int xx[] = {0,1,0,-1};
int yy[] = {1,0,-1,0};

//用于求蛇身每一节对于前一节的方向，0,1,2,3，分别表示右下左上
int check(int a,int b,int c,int d){
    if(c-a==0&&d-b==1) return 0;
    if(c-a==1&&d-b==0) return 1;
    if(c-a==0&&d-b==-1) return 2;
    if(c-a==-1&&d-b==0) return 3;
}

//初始输入+预处理
void init(){
    cin>>snakeHeadX>>snakeHeadY;
    int a=snakeHeadX,b=snakeHeadY,c,d;
    snakeBody=0;
    for(int i=0;i<snakeNum-1;i++){
        cin>>c>>d;
        snakeBody+=four[i]*check(a,b,c,d);
        a=c,b=d;
    }
    cin>>stNum;
    memset(ditu,true,sizeof ditu);
    for(int i=0;i<stNum;i++){
        cin>>a>>b;ditu[a][b]=false;
    }
}

//测试函数 可删除
void show(){
    cout<<n<<" "<<m<<" "<<snakeNum<<endl;
    cout<<snakeHeadX<<" "<<snakeHeadY<<" "<<snakeBody<<endl;
    for(int i=0;i<snakeNum-1;i++){
        int tmp = snakeBody % 4;
        cout<<tmp<<" ";
        snakeBody/=4;
    }cout<<endl;
    cout<<stNum<<endl;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++) cout<<ditu[i][j]<<" ";cout<<endl;
    }
}

//蛇头X,Y坐标 蛇的四进制表示  启发函数数值f（这里是蛇头与洞口（1,1）的曼哈顿距离）
struct node{
    int x,y,snake,step,f;
    node(int xx,int yy,int ssnake,int sstep):x(xx),y(yy),snake(ssnake),step(sstep){
        f=step+abs(x-1)+abs(y-1);
    }
    bool operator < (const node &a) const{
        return f > a.f;
    }
};

//这个函数是通过 蛇头坐标 蛇身四进制 来求 蛇身坐标数组 和 蛇尾对于前一节的方向
void snakeXY(int SX,int SY,int (&snakeX)[8],int (&snakeY)[8],int &c,int d){
    int x = SX,y = SY;
    for(int i=0;i<snakeNum-1;i++){
        int tmp = d % 4; d/=4;
        x+=xx[tmp],y+=yy[tmp];
        snakeX[i] = x ,snakeY[i] = y ;
        if(i==snakeNum-2) c = tmp;
    }
}

//判断蛇头是否能走(x,y)
bool checkN(int x,int y,int a[],int b[]){
    if(x<=0||x>n||y<=0||y>m||ditu[x][y]==false) return false;
    for(int i=0;i<snakeNum-1;i++){
        if(x==a[i]&&y==b[i]) return false;
    }
    return true;
}

//A*算法
int Astar(){
    memset(vis,false,sizeof vis);
    priority_queue<node> q;
    q.push(node(snakeHeadX,snakeHeadY,snakeBody,0));
    vis[snakeHeadX][snakeHeadY][snakeBody] = true;

    while(!q.empty()){
        node p = q.top();q.pop();
        if(p.x==1&&p.y==1) return p.step;

        //这里记录蛇身坐标 和 蛇尾方向
        int snakeX[8],snakeY[8],tail;
        snakeXY(p.x,p.y,snakeX,snakeY,tail,p.snake);

        //右、下、左、上
        for(int i=0;i<4;i++){
            int x = p.x + xx[i],y = p.y + yy[i];
            if(!checkN(x,y,snakeX,snakeY)) continue;
            //这里开始算新的方向四进制  去尾加头
            int body = p.snake - four[snakeNum-2]*tail;
            body*=4;
            if(i==0) body+=2;
            else if(i==1) body+=3;
            else if(i==2) body+=0;
            else body += 1;

            if(vis[x][y][body]) continue;
            vis[x][y][body] = true;
            q.push(node(x,y,body,p.step+1));
        }
    }
    return -1;
}

int main()
{
    four[0]=1;for(int i=1;i<7;i++) four[i] = four[i-1]*4;
    int _=1;
    while(cin>>n>>m>>snakeNum&&n&&m&&snakeNum){
        init();
        cout<<"Case "<<_++<<": ";
        cout<<Astar()<<endl;
    }
    return 0;
}

View Code

Bloxorz IPOJ - 3322

题意：游戏推一个由两个正方形组成的长方体，可以横着推也可以把长方体竖起来，然后地图由空白、紧固地、不坚固地（长方体不能立在上面，但可以横着站在上面）组成；问长方体从开始位置到目标位置的最短路径

算法：BFS 简单模拟题

思路：其实这题主要是判重，因为包括竖着与横着两个状态，横着由两个坐标表示，又因为地图最大为500，如果判重数组由两个坐标来维护，vis[X1][Y1][X2][Y2]，则是500的4次方，绝对MLE。这里就想到上一题的思路，只要记住一个坐标就行，另一个方块只要记住方向就可以了；然后判重数组就变为 vis[X1][Y1][方向] 只要开三维，而且 500*500*5 绝对不MLE。这里我方向是：0——直立，1——右，2——下，3——左，4——上。

易错点：这里我又是1A，模拟题可能就细节比较容易出错，不过如果你清楚思路，数据也过了，基本就ac了

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>

using namespace std;

const int INF = 0x3f3f3f3f;

int n,m;
int ditu[505][505];
bool vis[505][505][5];

int xx[] = {0,1,0,-1};
int yy[] = {1,0,-1,0};

//dir 0:直立 1~4 左下右上
int sX,sY,dir;
int tX,tY;

int check(int x,int y,int a,int b){
    if(a-x==0&&b-y==1) return 1;
    if(a-x==1&&b-y==0) return 2;
    if(a-x==0&&b-y==-1) return 3;
    if(a-x==-1&&b-y==0) return 4;
}

void init(){
    memset(ditu,0,sizeof ditu);
    dir =-1;
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++){
        char ch = getchar();if(ch=='\n') ch=getchar();
        if(ch=='X'){
            if(dir==-1) sX=i,sY=j,dir++;
            else dir=check(sX,sY,i,j);
            ditu[i][j]=1;
        }
        else if(ch=='O') tX=i,tY=j,ditu[i][j]=1;
        else if(ch=='.') ditu[i][j] = 1;
        else if(ch=='E') ditu[i][j] = 2;
    }
}

void show(){
    cout<<sX<<" "<<sY<<" "<<dir<<" "<<tX<<" "<<tY<<endl;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++) cout<<ditu[i][j]<<" ";cout<<endl;
    }
}

struct node{
    int x,y,d,step;
    node(int xx,int yy,int dd,int sstep):x(xx),y(yy),d(dd),step(sstep) {}
    bool check(){
        if(d==0&&x==tX&&y==tY) return true;
        return false;
    }
};

bool checkXY(int a,int b,int z){
    if(a<=0||a>n||b<=0||b>m) return false;
    if(ditu[a][b]==0) return false;
    if(z==0&&ditu[a][b]==2) return false;
    if(z==0) return true;
    int c,d;
    if(z==1) c=a,d=b+1;
    else if(z==2) c=a+1,d=b;
    else if(z==3) c=a,d=b-1;
    else if(z==4) c=a-1,d=b;
     if(c<=0||c>n||d<=0||d>m) return false;
    if(ditu[c][d]==0) return false;
    return true;
}

int BFS(){
    queue<node> q;
    q.push(node(sX,sY,dir,0));
    memset(vis,false,sizeof vis);
    vis[sX][sY][dir] = true;

    while(!q.empty()){
        node p = q.front();q.pop();
        if(p.check()) return p.step;
        //直立情况====================
        if(p.d==0){
            for(int i=0;i<4;i++){
                int x = p.x + xx[i], y = p.y + yy[i];
                int d = i + 1;
                if(!checkXY(x,y,d)) continue;
                if(vis[x][y][d]) continue;
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
        }
        //方向为1===============
        if(p.d==1){
            int x,y,d;
             //右================
             x = p.x , y = p.y+2, d = 0;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //下=================
            x = p.x + 1, y = p.y ,d = 1;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //左================
             x = p.x , y = p.y-1, d = 0;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //上=================
            x = p.x - 1, y = p.y ,d = 1;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
        }
        //方向为2===============
        if(p.d==2){
            int x,y,d;
             //右================
             x = p.x , y = p.y+1, d = 2;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //下=================
            x = p.x + 2, y = p.y ,d = 0;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //左================
             x = p.x , y = p.y-1, d = 2;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //上=================
            x = p.x - 1, y = p.y ,d = 0;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
        }
        //方向为3===============
        if(p.d==3){
            int x,y,d;
             //右================
             x = p.x , y = p.y+1, d = 0;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //下=================
            x = p.x + 1, y = p.y ,d = 3;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //左================
             x = p.x , y = p.y-2, d = 0;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //上=================
            x = p.x - 1, y = p.y ,d = 3;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
        }
        //方向为4===============
        if(p.d==4){
            int x,y,d;
             //右================
             x = p.x , y = p.y+1, d = 4;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //下=================
            x = p.x + 1, y = p.y ,d = 0;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //左================
             x = p.x , y = p.y-1, d = 4;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
            //上=================
            x = p.x - 2, y = p.y ,d = 0;
            if(checkXY(x,y,d)&&!vis[x][y][d]){
                vis[x][y][d] = true;
                q.push(node(x,y,d,p.step+1));
            }
        }
    }
    return -1;
}

int main()
{
    while(cin>>n>>m&&n&&m){
        init();//show();
        int ans = BFS();
        if(ans==-1) puts("Impossible");
        else cout<<ans<<endl;
    }
    return 0;
}

View Code

An interesting mobile gameHDU - 3295

题意：

1、一个最大6*6的方阵中有4种颜色的方块。

2、然后玩家可以进行点击颜色方块的操作，每次点击都会消除互相连接并且颜色相同的方块。

3、消除方块之后，向下向左靠的原则，如果一个列都空的话，右边的列就会向左补上。

4、求消除所有颜色方块的最少操作数

算法：BFS+最小生成树/DFS

思路：一道模拟题

　　　求最少操作数，可以DFS搜索所有情况，或者BFS求最少。因为这里每个点只要记录步数+方阵状态，所以BFS的存储压力不大。我这里使用string来压缩状态，然后也是通过map来进行入队判重。

　　　然后点击消除方块，则可以通过最小生成树的原理来区分出被消除的方块；对这些方块进行标记，来进行第二重的操作判重；

最后就是消除方块后的整合工作

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <map>

using namespace std;

const int INF = 0x3f3f3f3f;

int n,m;
string str;
int xx[]={0,0,-1,1};
int yy[]={1,-1,0,0};

void init(){
    str="";
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            int a;cin>>a;str+=('0'+a);
        }
    }
}

struct node{
    string s;int step;
    node(string ss,int sstep):s(ss),step(sstep) {}
    bool check(){
        for(int i=0;i<s.size();i++) if(s[i]!='0') return false;
        return true;
    }
};

int temp[6][6],ttem[6][6];
bool ck[6][6];

void make(string s){
    int num = 0;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++) temp[i][j] = s[num++] - '0';
}

void dfs(int a,int b,int c){
    for(int i=0;i<4;i++){
        int x = a + xx[i] , y = b + yy[i];
        if(x<0||x>=n||y<0||y>=m||temp[x][y]!=c||ck[x][y]) continue;
        ck[x][y]=true;
        ttem[x][y]=0;
        dfs(x,y,c);
    }
}

string remake(){
    int a[6][6];
    memset(a,0,sizeof a);
    int aX,aY=0;
    for(int j=0;j<m;j++){
        bool flag = false;
        aX = n-1;
        for(int i=n-1;i>=0;i--){
            if(ttem[i][j]==0) continue;
            flag=true;
            a[aX--][aY] = ttem[i][j];
        }
        if(flag) aY++;
    }
    string s = "";
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++) s+=('0'+a[i][j]);
    return s;
}

int bfs(){
    queue<node> q;q.push(node(str,0));
    map<string,bool> mp;mp[str]=true;
    while(!q.empty()){
        node p = q.front();q.pop();
        if(p.check()) return p.step;
        memset(ck,false,sizeof ck);
        make(p.s);
        for(int j=0;j<m;j++){
            for(int i=n-1;i>=0;i--){
                if(temp[i][j]==0) break;
                if(ck[i][j]) continue;
                ck[i][j]=true;
                for(int i=0;i<n;i++) for(int j=0;j<m;j++) ttem[i][j] = temp[i][j];
                ttem[i][j]=0;
                dfs(i,j,temp[i][j]);
                string sss = remake();
                if(mp[sss]) continue;
                mp[sss] = true;
                q.push(node(sss,p.step+1));
            }
        }

    }
}

int main()
{
    while(cin>>n>>m&&n&&m){
            init();
            cout<<bfs()<<endl;
    }
    return 0;
}

View Code

Continuous Same Game (1)HDU - 2258

题意：和上一题一样是消除方块，下面空就下降，一列空就向左靠；题目规则是找最大块进行消除，同等大小则选最上面最左边的进行消除————贪心算法；

算法：模拟题

思路：从左上往右下搜索，找最大块进行消除

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <map>

using namespace std;

const int INF = 0x3f3f3f3f;

int n,m,ans;
char ch[20][20];
int ditu[20][20];
bool flag[20][20];
int xx[]={0,0,-1,1};
int yy[]={1,-1,0,0};

void init(){
    for(int i=0;i<n;i++) cin>>ch[i];
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++) ditu[i][j] = ch[i][j] - '0';
}

int dfs(int a,int b,int c){
    int ans = 0;
    for(int i=0;i<4;i++){
        int x = a + xx[i] ,  y = b + yy[i];
        if(x<0||x>=n||y<0||y>=m||ditu[x][y]!=c) continue;
        if(flag[x][y]) continue;flag[x][y]=true;
        ans++;ans+=dfs(x,y,c);
    }
    return ans;
}

void dfs2(int a,int b,int c){
    for(int i=0;i<4;i++){
        int x = a + xx[i] ,  y = b + yy[i];
        if(x<0||x>=n||y<0||y>=m||ditu[x][y]!=c) continue;
        ditu[x][y]=0;
        dfs2(x,y,c);
    }
}

void remake(){
    int ans[20][20];
    memset(ans,0,sizeof ans);
    int ansX,ansY=0;
    for(int j=0;j<m;j++){
        bool flag = false;
        ansX = n-1;
        for(int i=n-1;i>=0;i--){
            if(ditu[i][j]==0) continue;
            flag=true;
            ans[ansX--][ansY] = ditu[i][j];
        }
        if(flag) ansY++;
    }
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++) ditu[i][j] = ans[i][j];
}

void show(){
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++) cout<<ditu[i][j];cout<<endl;
    }
}

int run(){
    int ans = 0;
    bool fg=false;
    int maxNum = 1, aX,aY;
    memset(flag,false,sizeof flag);
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(ditu[i][j]==0) continue;
            if(flag[i][j]) continue;
            flag[i][j] = true;
            int cnt = dfs(i,j,ditu[i][j])+1;
            if(maxNum<cnt) {maxNum = cnt , aX = i, aY = j,fg = true;}
        }
    }
    if(fg) {
            ans += maxNum*(maxNum-1);
            int tnt = ditu[aX][aY];
            ditu[aX][aY]=0;
            dfs2(aX,aY,tnt);
            remake();
            ans+=run();
    }
    return ans;
}


int main()
{
    while(cin>>n>>m&&n&&m){
        init();
        cout<<run()<<endl;
    }
    return 0;
}

View Code

Continuous Same Game (2)HDU - 2259

题意：上题的延续，需要一个比贪心算法还优秀的算法。

算法：优先队列+暴力评估

思路：1.首先这题我没有想出来，是看别人博客学的；

　　　2.一个node状态存储地图，得分，评估价值，答案等；答案是从初始状态到现阶段的决策数组，即本体答案；得分是从初始状态到现阶段的所有清除方块后的n*（n-1）的总和；

　　　3.优先队列通过评估价值来排序，价值最高则先出队；评估价值则是直接从现状态，在不移动方块前提下，计算所有可能被清除的方块堆的得分总和，再加上现阶段得分---------就是一种粗略计算最终得分数的方法

4.这里应该是博客大佬自己慢慢测试出来的，就是队列bfs循环至少要在24步内解决。少于24步不能得出答案，多于不超时也行。即测试数据中最大的答案是24个步骤的。

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <map>

using namespace std;

const int INF = 0x3f3f3f3f;

int n,m;
int xx[]={0,0,-1,1};
int yy[]={1,-1,0,0};
char ch[20][20];

struct node{
    int ditu[20][20];//地图
    int ans,val;//得分（从最初到这个状态）、价值（用于优先队列排序）
    int step,X[26],Y[26];//答案
    //以下都适用于价值评估函数eval所需要
    int cnt,temp[20][20];
    bool vis[20][20];

    bool operator < (const node &a) const{
        return val<a.val;
    }
    //坐标(a,b)向外扩展清零
    void  clean(int a,int b,int c){
        for(int i=0;i<4;i++){
            int x = a + xx[i] ,  y = b + yy[i];
            if(x<0||x>=n||y<0||y>=m||ditu[x][y]!=c) continue;
            ditu[x][y]=0;
            clean(x,y,c);
        }
    }
    //清零之后的向左向下靠齐
    void remake(){
        int tmp[20][20];
        memset(tmp,0,sizeof tmp);
        int tmpX,tmpY=0;
        for(int j=0;j<m;j++){
            bool flag = false;
            tmpX = n-1;
            for(int i=n-1;i>=0;i--){
                if(ditu[i][j]==0) continue;
                flag=true;
                tmp[tmpX--][tmpY] = ditu[i][j];
            }
            if(flag) tmpY++;
        }
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++) ditu[i][j] = tmp[i][j];
    }
    //用于计算cnt，即扎堆数量
    void  clean2(int a,int b,int c){
        for(int i=0;i<4;i++){
            int x = a + xx[i] ,  y = b + yy[i];
            if(x<0||x>=n||y<0||y>=m||temp[x][y]!=c||!vis[x][y]) continue;
            temp[x][y]=0,cnt++;
            clean2(x,y,c);
        }
    }
    //价值评估函数
    void eval(){
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++) temp[i][j]=ditu[i][j];
        memset(vis,true,sizeof vis);
        val = ans;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++){
                if(temp[i][j]==0) continue;
                int tmp = temp[i][j];
                temp[i][j]=0;
                cnt=1;
                clean2(i,j,tmp);
                if(cnt>1){
                    temp[i][j]=cnt;vis[i][j]=false;
                    val += cnt*(cnt-1);
                }
        }
    }
}t,ans;
//测试用
void show(){
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++) cout<<t.temp[i][j]<<" ";
        cout<<endl;
    }cout<<t.val<<endl;
}
//输入
void init(){
    for(int i=0;i<n;i++) cin>>ch[i];
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++) t.ditu[i][j] = ch[i][j] - '0';
    t.ans=0, t.step=0;t.eval();
    //show();
}

void run(){
    ans.ans=0;
    priority_queue<node> q;
    q.push(t);
    int stepNum=0;
    while(!q.empty()){
        node p = q.top();q.pop();
        if(ans.ans<p.ans) ans=p;
        if(++stepNum>24) break;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++) if(p.temp[i][j]){
                    node tp = p;
                    p.clean(i,j,p.ditu[i][j]);
                    p.ditu[i][j]=0;
                    p.remake();
                    p.X[p.step]=i,p.Y[p.step]=j,p.step++;
                    p.ans+=p.temp[i][j]*(p.temp[i][j]-1);
                    p.eval();
                    q.push(p);
                    p=tp;
        }
    }
}

int main()
{
    while(cin>>n>>m&&n&&m){
        init();
        run();
        cout<<ans.step<<endl;
        for(int i=0;i<ans.step;i++) cout<<ans.X[i]<<" "<<ans.Y[i]<<endl;
    }
    return 0;
}

View Code

Prison Break HDU - 3681

题意：给你一个n,m地图，然后F是起点，G是充电点，Y是开关，要把所有开关关掉才能过关，D是不可穿越的障碍；初始状态下电池是满的，然后没走一部少一格电量，问主角至少要带多少电量的电池包才可以过关。

算法：BFS预处理距离+二分查找答案+暴力枚举测试是否过关

思路：首先，本题找最少可过关的电池量，我们可从0~15*15来二分查找，可过关的就向下找，否则向上，临界点则为答案。

　　　然后，关键点是F\G\Y。F、Y是必经的点，G点是充电点，用于中途补给。G、Y总和小于15，加上F最多就是15，所以可以通过15位二进制数来表示状态。暴力从0~1<<15枚举所有可能情况，然后找到一个状态，覆盖所有Y点和F点，然后他的电量为非负数则该电量可通过。

易错点：需要先预处理，BFS出所有F\G\Y点之间的距离。

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <map>

using namespace std;

const int INF = 0x3f3f3f3f;

int n,m;
char ch[15][16];
int dis[15][15][15][15];
int dp[1<<15][15];
int finalState,stateNum,startNum;
int xx[] = {1,-1,0,0};
int yy[] = {0,0,-1,1};

struct node{
    int x,y;
    node() {}
    node(int a,int b):x(a),y(b) {}
}po[15];

void BFS(int nn){
    queue<node> q;
    int sx = po[nn].x , sy = po[nn].y;
    dis[sx][sy][sx][sy]= 0;
    q.push(po[nn]);
    while(!q.empty()){
        node p = q.front();q.pop();
        for(int i=0;i<4;i++){
            int x = p.x+xx[i], y = p.y+yy[i];
            if(x<0||x>=n||y<0||y>=m||ch[x][y]=='D') continue;
            if(dis[sx][sy][x][y]==-1){
                dis[sx][sy][x][y] = dis[sx][sy][p.x][p.y]+1;
                q.push(node(x,y));
            }
        }
    }
}

void init(){
    finalState=0;stateNum=0;
    for(int i=0;i<n;i++) cin>>ch[i];
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++){
            if(ch[i][j]=='S'||ch[i][j]=='D') continue;
            if(ch[i][j]=='F') startNum=stateNum;
            po[stateNum] = node(i,j);
            if(ch[i][j]=='F'||ch[i][j]=='Y') finalState+=1<<stateNum;
            stateNum++;
    }
    memset(dis,-1,sizeof dis);
    for(int i=0;i<stateNum;i++) BFS(i);
}

void show(){
    int t = 1<<stateNum;
    cout<<stateNum<<" "<<startNum<<" "<<finalState<<" "<<t<<endl;
    for(int i=0;i<stateNum;i++){
        int x = po[i].x , y = po[i].y;
        for(int j=0;j<stateNum;j++){
            int a=po[j].x, b=po[j].y;
            cout<<dis[x][y][a][b]<<" ";
        }cout<<endl;
    }
}

bool check(int cup){
    memset(dp,-1,sizeof dp);
    dp[1<<startNum][startNum] = cup;
    for(int st=0;st<1<<stateNum;st++){
        for(int i=0;i<stateNum;i++){
            if(st&1<<i==0 || dp[st][i]==-1) continue;
            if((st&finalState&finalState)==finalState) return true;
            for(int j=0;j<stateNum;j++){
                int dist = dis[po[i].x][po[i].y][po[j].x][po[j].y];
                if(i==j||st&1<<j||dist==-1||dp[st][i]-dist<0) continue;
                int newSt = st+(1<<j);
                dp[newSt][j] = max(dp[st][i] - dist,dp[newSt][j]);
                if(ch[po[j].x][po[j].y]=='G') dp[newSt][j] = cup;
            }
        }
    }
    return false;
}

int run(){
    int left = 0, right = n*m;
    while(left<=right){
        int mid = left + right >>1;
        if(check(mid)) right = mid-1;
        else left = mid +1;
    }
    if(left>n*m) return -1;
    return left;
}

int main()
{
    while(cin>>n>>m&&n&&m){
        init();//show();
        cout<<run()<<endl;
    }
    return 0;
}

View Code

Dearboy's PuzzlePOJ - 2308

题意：连连看，给你一幅地图然后，你只能用题目图中的连线消除。（这里看题目，有个疑惑就是连线可以走在图外面吗？我试着不走外面来消除，然后ac了。所以连线不能在外面的）

算法：DFS+BFS

思路：1.这里只需求是否可以把图案全部消除，所以DFS出一个答案就行了，顺便节省空间。

　　　2.用char字符数组存地图，然后末尾加'\0'，形成字符串，然后用map<string,bool> 来判重。

　　　3.测试用例一知道，需要记录A、B、C、D的数量，存在单个字符奇数总和就可直接 no，这里要记录，就顺便将字符记录在vector中，方便后面使用，加快速度。

　　　4.测试用例二知道，这种情况是无解的，所以也需要状态判断，当dfs走到这一步可以直接 no

　　　5.DFS从一个字母字符开始，用BFS找出所有可以消除的同字母字符，这里BFS通过从一个字符开始，只走三层，没走一层都在四个方向上，循环走到底，找出所有可能。

易错点：测试用例二的情况容易忽略掉。

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <map>

using namespace std;

const int INF = 0x3f3f3f3f;

int n,m;
char ditu[111];int dituNum;
char ditu2[13][13];
int Anum,Bnum,Cnum,Dnum;
map<string,bool> mp;

struct node{
    int x,y,z;
    node(int a,int b,int c):x(a),y(b),z(c) {}
};
vector<node> v;

void init(){
    mp.clear();v.clear();
    dituNum=0,Anum=0,Bnum=0,Cnum=0,Dnum=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            char ch = getchar();
            while(ch==' '||ch=='\n') ch = getchar();
            ditu[dituNum++]=ch;
            ditu2[i][j]=ch;
            if(ch!='*') v.push_back(node(i,j,0));
            if(ch=='A') Anum++;
            else if(ch=='B') Bnum++;
            else if(ch=='C') Cnum++;
            else if(ch=='D') Dnum++;
        } ditu[dituNum]='\0';
    mp[ditu] = true;
}

bool check(){
    if(Anum==0&&Bnum==0&&Cnum==0) return true;
    if(Anum==0&&Bnum==0&&Dnum==0) return true;
    if(Anum==0&&Dnum==0&&Cnum==0) return true;
    if(Bnum==0&&Dnum==0&&Cnum==0) return true;
    return false;
}

bool check3(char a,char b){
    for(int i=0;i<v.size();i++){
        int x = v[i].x , y = v[i].y;
        if(ditu2[x][y]==a){
                if(ditu2[x+1][y+1]==a&&ditu2[x+1][y]==b&&ditu2[x][y+1]==b) return true;
                return false;
        }else if(ditu2[x][y]==b){
                if(ditu2[x+1][y+1]==b&&ditu2[x+1][y]==a&&ditu2[x][y+1]==a) return true;
                return false;
        }
    }
}

bool check2(){
    if(Anum==2&&Bnum==2&&check3('A','B')) return true;
    if(Anum==2&&Cnum==2&&check3('A','C')) return true;
    if(Anum==2&&Dnum==2&&check3('A','D')) return true;
    if(Cnum==2&&Bnum==2&&check3('C','B')) return true;
    if(Dnum==2&&Bnum==2&&check3('D','B')) return true;
    if(Cnum==2&&Dnum==2&&check3('C','D')) return true;
    return false;
}

int xx[] = {1,0,0,-1};
int yy[] = {0,1,-1,0};

vector<node> BFS(int u,int o){
    vector<node> vv;
    bool vis[13][13];
    memset(vis,true,sizeof vis);
    queue<node> q;
    q.push(node(u,o,0)); vis[u][o] = false;
    while(!q.empty()){
        node p = q.front();q.pop();
        if(p.z==3) break;
        for(int i=0;i<4;i++){
            int x = p.x , y = p.y;
            while(1){
                x+= xx[i], y+= yy[i];
                if(x<1||x>n||y<1||y>m) break;
                if(!vis[x][y]) break;
                vis[x][y]=false;
                if(ditu2[x][y]=='*') q.push(node(x,y,p.z+1));
                else if(ditu2[x][y]==ditu2[u][o]) {vv.push_back(node(x,y,0));break;}
                else break;
            }
        }
    }
    return vv;
}

bool dfs(){
    vector<node> vv;
    if(check()) return true;
    if(check2()) return false;
    for(int i=0;i<v.size();i++){
        int x = v[i].x , y = v[i].y;
        if(ditu2[x][y]=='*') continue;
        char c = ditu2[x][y];
        vv = BFS(x,y);
        for(int j=0;j<vv.size();j++){
            int u = vv[j].x , o =vv[j].y;
            int a = (x-1)*m + y-1 ,b = (u-1)*m + o-1;
            ditu[a]='*' , ditu[b]='*';
            if(mp[ditu]) {ditu[a]=c , ditu[b]=c;continue;}
            mp[ditu] = true;
            ditu2[x][y]='*' , ditu2[u][o]='*';
            if(c=='A') Anum-=2;else if(c=='B') Bnum-=2;else if(c=='C') Cnum-=2;else Dnum-=2;
            if(dfs()) return true;
            if(c=='A') Anum+=2;else if(c=='B') Bnum+=2;else if(c=='C') Cnum+=2;else Dnum+=2;
            ditu2[x][y]=c , ditu2[u][o]=c;
            ditu[a]=c , ditu[b]=c;
        }
    }
    return false;
}

int main()
{
    while(cin>>n>>m&&n&&m){
        init();
        if(Anum%2||Bnum%2||Cnum%2||Dnum%2) {puts("no");continue;}
        if(dfs()) puts("yes");
        else puts("no");
    }
    return 0;
}

View Code

Cleaning Robot POJ - 2688

题意：清洁机器人之求在有障碍的多个脏地板的地图上，清理完需要最短的步数。答案不存在输出-1

算法：BFS预处理+DFS

思路：1.因为都要清理完，所以起点和脏地板都是必经，这题和上面的Prison Break HDU - 3681 很像，所以这里就直接BFS先预处理这些必经点的距离

　　　2.DFS枚举所有顺序，然后用答案大小剪枝

易错点：这里数组空间要开大一点，我wrong了几次。

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 
  9 using namespace std;
 10 
 11 const int INF = 0x3f3f3f3f;
 12 
 13 int n,m;
 14 char ditu[21][21];
 15 struct node{
 16     int x,y;
 17     node() {}
 18     node(int a,int b):x(a),y(b) {}
 19 }po[12];
 20 int stNum,allNum;
 21 int dist[21][21][21][21];
 22 int xx[]={1,-1,0,0};
 23 int yy[]={0,0,-1,1};
 24 
 25 void BFS(int a){
 26     queue<node> q;
 27     int u = po[a].x, v = po[a].y;
 28     q.push(node(u,v));
 29     dist[u][v][u][v] =0 ;
 30     while(!q.empty()){
 31         node p = q.front();q.pop();
 32         for(int i=0;i<4;i++){
 33             int x = p.x + xx[i] , y = p.y + yy[i];
 34             if(x<0||x>=n||y<0||y>=m||ditu[x][y]=='x') continue;
 35             if(dist[u][v][x][y]>dist[u][v][p.x][p.y]+1){
 36                 dist[u][v][x][y]=dist[u][v][p.x][p.y]+1;
 37                 q.push(node(x,y));
 38             }
 39         }
 40     }
 41 }
 42 
 43 void init(){
 44     allNum=0;
 45     for(int i=0;i<n;i++)
 46     for(int j=0;j<m;j++){
 47         char ch = getchar();while(ch==' '||ch=='\n') ch=getchar();
 48         ditu[i][j]=ch;
 49         if(ditu[i][j]=='*')  po[allNum].x = i, po[allNum++].y  = j;
 50         else if(ditu[i][j]=='o')  stNum = allNum, po[allNum].x = i, po[allNum++].y  = j;
 51     }
 52     memset(dist,INF,sizeof dist);
 53     for(int i=0;i<allNum;i++) BFS(i);
 54 }
 55 
 56 bool vis[12];
 57 int ans;
 58 
 59 bool check(){
 60     for(int i=0;i<allNum;i++) if(!vis[i]) return false;
 61     return true;
 62 }
 63 
 64 void DFS(int p,int a){
 65     if(a>=ans) return;
 66     if(check()) {ans = min(ans,a);return ;}
 67     int u = po[p].x, v =po[p].y;
 68     for(int i=0;i<allNum;i++){
 69         if(i==p||vis[i]) continue;
 70         vis[i] = true;
 71         int x = po[i].x, y =po[i].y;
 72         DFS(i,a+dist[u][v][x][y]);
 73         vis[i]=false;
 74     }
 75     return ;
 76 }
 77 
 78 void show(){
 79     for(int i=0;i<n;i++){
 80         for(int j=0;j<m;j++) cout<<ditu[i][j]<<" ";cout<<endl;}
 81     for(int i=0;i<allNum;i++){
 82         int u = po[i].x, v = po[i].y;
 83         cout<<i<<" "<<u<<" "<<v<<endl;
 84         for(int j=0;j<allNum;j++){
 85             int x = po[j].x, y = po[j].y;
 86             cout<<dist[u][v][x][y]<<" ";
 87         }cout<<endl;
 88     }
 89 }
 90 
 91 int main()
 92 {
 93     while(cin>>m>>n&&n&&m){
 94         init();//show();
 95         memset(vis,false,sizeof vis);
 96         vis[stNum] = true;
 97         ans = INF;
 98         DFS(stNum,0);
 99         cout<<(ans==INF?-1:ans)<<endl;
100     }
101     return 0;
102 }

View Code

RobotPOJ - 1376

题意：有一个机器人，一个人就占着四个格子，然后有障碍物，本身有个方向。每个命令执行需要一秒，命令分为90度转向，或者在本来方向上前进1\2\3步。

算法：BFS

易错点：这题没什么思路，按着题目进行模拟BFS就过，该注意的就是，机器人每次操作，都只能90度转向，然后只能前进一步或者两步或者三步，只要遇到障碍物就不能前进了。判重直接三维，坐标+方向。

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 
 9 using namespace std;
10 
11 const int INF = 0x3f3f3f3f;
12 
13 int n,m;
14 int ditu[51][51];
15 int sx,sy,tx,ty,fx;
16 int xx[]={-1,0,1,0};
17 int yy[]={0,1,0,-1};
18 int ffx[4][2] = {{1,3},{0,2},{1,3},{0,2}};
19 bool vis[51][51][5];
20 
21 int check(string ch){
22     if(ch.compare("north")==0) return 0;
23     else if(ch.compare("east")==0) return 1;
24     else if(ch.compare("south")==0) return 2;
25     return 3;
26 }
27 
28 void init(){
29     for(int i=1;i<=n;i++)
30         for(int j=1;j<=m;j++) cin>>ditu[i][j];
31     string s;
32     cin>>sx>>sy>>tx>>ty>>s;
33     fx = check(s);
34 }
35 
36 struct node{
37     int x,y,z,step;
38     node(int a,int b,int c,int d):x(a),y(b),z(c),step(d) {}
39     bool checkIn(){
40         return x==tx&&y==ty;
41     }
42 };
43 
44 bool check2(int x,int y){
45     int x2 = x+1 , y2 = y, x3 = x, y3 = y+1, x4 = x+1, y4 = y+1;
46     if(x<=0||x>n||y<=0||y>m||ditu[x][y]==1) return true;
47     if(x2<=0||x2>n||y2<=0||y2>m||ditu[x2][y2]==1) return true;
48     if(x3<=0||x3>n||y3<=0||y3>m||ditu[x3][y3]==1) return true;
49     if(x4<=0||x4>n||y4<=0||y4>m||ditu[x4][y4]==1) return true;
50     return false;
51 }
52 
53 int bfs(){
54     memset(vis,false,sizeof vis);
55     queue<node>   q;
56     vis[sx][sy][fx] = true;
57     q.push(node(sx,sy,fx,0));
58     while(!q.empty()){
59         node p = q.front();q.pop();
60         if(p.checkIn()) return p.step;
61         //90度转向--------------------------------
62         for(int i=0;i<2;i++) {
63             int fffx = ffx[p.z][i];
64             if(vis[p.x][p.y][fffx]) continue;
65             vis[p.x][p.y][fffx]=true;
66             q.push(node(p.x,p.y,fffx,p.step+1));
67         }
68         //移动--------------------------------
69         for(int i=1;i<=3;i++){
70             int x = p.x+i*xx[p.z], y= p.y+i*yy[p.z];
71             if(check2(x,y)) break;
72             if(vis[x][y][p.z]) continue;
73             vis[x][y][p.z] = true;
74             q.push(node(x,y,p.z,p.step+1));
75         }
76     }
77     return -1;
78 }
79 
80 int main()
81 {
82     while(cin>>n>>m&&n&&m){
83         init();
84         cout<<bfs()<<endl;
85     }
86     return 0;
87 }

View Code

这题有意思的地方是，我一开始用Astar算法，用曼哈顿距离做评估函数，然后wrong了。测试数据一看，就是判重问题，因为存在障碍物，导致不完美答案先一步入队了。后面乱改一通还是ac了。

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 
 9 using namespace std;
10 
11 const int INF = 0x3f3f3f3f;
12 
13 int n,m;
14 int ditu[51][51];
15 int sx,sy,tx,ty,fx;
16 int xx[]={-1,0,1,0};
17 int yy[]={0,1,0,-1};
18 int ffx[4][2] = {{1,3},{0,2},{1,3},{0,2}};
19 int vis[51][51][5];
20 
21 int check(string ch){
22     if(ch.compare("north")==0) return 0;
23     else if(ch.compare("east")==0) return 1;
24     else if(ch.compare("south")==0) return 2;
25     return 3;
26 }
27 
28 void init(){
29     for(int i=1;i<=n;i++)
30         for(int j=1;j<=m;j++) cin>>ditu[i][j];
31     string s;
32     cin>>sx>>sy>>tx>>ty>>s;
33     fx = check(s);
34 }
35 
36 struct node{
37     int x,y,z,step,f;
38     node(int a,int b,int c,int d):x(a),y(b),z(c),step(d) {
39         f = d + abs(a-tx) + abs(b-ty);
40     }
41     bool operator < (const node &a) const{
42         //if(f==a.f) return step>a.step;
43         return f>a.f;
44     }
45     bool checkIn(){
46         return x==tx&&y==ty;
47     }
48 };
49 
50 bool check2(int x,int y){
51     int x2 = x+1 , y2 = y, x3 = x, y3 = y+1, x4 = x+1, y4 = y+1;
52     if(x<=0||x>n||y<=0||y>m||ditu[x][y]==1) return true;
53     if(x2<=0||x2>n||y2<=0||y2>m||ditu[x2][y2]==1) return true;
54     if(x3<=0||x3>n||y3<=0||y3>m||ditu[x3][y3]==1) return true;
55     if(x4<=0||x4>n||y4<=0||y4>m||ditu[x4][y4]==1) return true;
56     return false;
57 }
58 
59 int bfs(){
60     memset(vis,INF,sizeof vis);
61     priority_queue<node>   q;
62     vis[sx][sy][fx] = 0;
63     q.push(node(sx,sy,fx,0));
64     int ans = INF;
65     while(!q.empty()){
66         node p = q.top();q.pop();
67         if(ans<=p.step) continue;
68         if(p.checkIn()) {ans = min(ans,p.step);continue;}
69         //90度转向--------------------------------
70         for(int i=0;i<2;i++) {
71             int fffx = ffx[p.z][i];
72             if(vis[p.x][p.y][fffx]!=INF&&vis[p.x][p.y][fffx]<=p.step+1) continue;
73             vis[p.x][p.y][fffx]=p.step+1;
74             q.push(node(p.x,p.y,fffx,p.step+1));
75         }
76         //移动--------------------------------
77         for(int i=1;i<=3;i++){
78             int x = p.x+i*xx[p.z], y= p.y+i*yy[p.z];
79             if(check2(x,y)) break;
80             if(vis[x][y][p.z]!=INF&&vis[x][y][p.z]<=p.step+1) continue;
81             vis[x][y][p.z] = p.step+1;
82             q.push(node(x,y,p.z,p.step+1));
83         }
84     }
85     return ans==INF?-1:ans;
86 }
87 
88 int main()
89 {
90     while(cin>>n>>m&&n&&m){
91         init();
92         cout<<bfs()<<endl;
93     }
94     return 0;
95 }

View Code

生日蛋糕OpenJ_Bailian - 1190

题意：给你一个固定的体积N，和层数M，并且蛋糕都是由圆柱体构成，下面一层R、H都要大于上面一层的；求蛋糕最大表面积Q（不算底部且除了Q外，其他数字都是正整数）

算法：数论+DFS

思路：说实话，不太懂怎么下手，算公式算很久把自己绕进去了。后面看了大神博客https://blog.csdn.net/weixin_46295292/article/details/105853440，原来需要在最大值、最小值入手。

　　　1.首先需要枚举最底层R1，这里因为R1>R2>...>RM，又因为这些R都是正整数，所以R1>=M；因为1^3+2^3+...+n^3=[n(n+1)/2]^2，所以通过已知N，当Rm=1，Hm=1，Rm-1=2，Hm-1=2类推的情况下，并且H1=M的时候 R1最大为sqrt( [4N-M^2*(M-1)^2]/(4*M));

　　　2.已知R1，相同情况下同理，保持底部体积最大求H1，且H1>=M；

　　　3.通过范围枚举R1，H1开启dfs（int r，int h ， int floor， int v，int s）

　　　4.dfs出队条件：1）f到了M层，判断v是否刚好为N，然后比较s，记录答案；2) 层数大于M或者dfs中s小于答案可以直接跳出 3）最小剩余体积大于 N-v 4）最大剩余体积小于 N-v

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 
 9 using namespace std;
10 
11 const int INF = 0x3f3f3f3f;
12 
13 int N,M;
14 int ans=INF;
15 
16 int minV(int f){
17     f = M - f;
18     return f*f*(f+1)*(f+1)/4;
19 }
20 
21 int maxV(int r,int h,int f){
22     int v = 0;
23     for(int R = r-1 , H = h-1;f<M;f++,R--,H--){
24         v+=R*R*H;
25     }
26     return v;
27 }
28 
29 void dfs(int r,int h,int f,int v,int s){
30     if(f==M&&v==N&&s<ans){
31         ans = s;return ;
32     }
33     if(f>M||s>=ans) return ;
34     if(minV(f)+v>N) return;
35     if(maxV(r,h,f)+v<N) return;
36     for(int R = r - 1;R>=M-f;R--)
37         for(int H=h-1;H>=M-f;H--) dfs(R,H,f+1,v+R*R*H,s+2*R*H);
38 }
39 
40 void run(){
41     int ttem = (4*N-(M-1)*(M-1)*M*M);
42     for(int r=M;r*r<=ttem/(4*M);r++){
43         for(int h =ttem/(4*r*r);h>=M;h--){
44             dfs(r,h,1,r*r*h,r*r+2*r*h);
45         }
46     }
47 }
48 
49 int main()
50 {
51     cin>>N>>M;
52     run();
53     cout<<(ans==INF?0:ans)<<endl;
54     return 0;
55 }

View Code

聪明的打字员POJ - 1184

题意：给你一个6位数打乱顺序的密码，然后你可以有6种操作：光标下的数字和位置1或者6交换、光标下的数字加一，光标的左右移动

算法：BFS

思路：正常BFS会TLE，所以开始构思，一开始思考是Astar，然后发现情况很复杂，影响结果的因素太多了，大概就是两种情况，一种就是单纯位数上加减，第二种就是考虑加减之后通过交换操作来进行交换，但是光标移动会消耗操作数。实在想不到，看了别人的博客。http://www.manongjc.com/detail/23-somyumfbupbiuxd.html

　　因为移动光标只对交换有影响，而且交换操作局限在于交换两个数的距离，存在很多无效操作，所以博主思路在于尽可能减少光标移动操作，加减优先于交换，而交换也是因为更接近于答案才进行对位置1和6的交换，优先服务于对2~5位置的需求，从左到右，2满足了，在移动到3，3满足了再移动4，...最后到位置6，可以都在位置6实现位置1和6的满足。

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 
  9 using namespace std;
 10 
 11 const int INF = 0x3f3f3f3f;
 12 
 13 int s[7],t[7],ss,tt;
 14 bool vis[1000001][6];
 15 
 16 int getNum(int a[7]){
 17     int ans = 0;
 18     for(int i=0;i<6;i++) ans*=10,ans+=a[i];
 19     return ans;
 20 }
 21 
 22 struct node{
 23     int a[7],step,gb;
 24     node(int b[],int c,int d){
 25         for(int i=0;i<6;i++) a[i]=b[i];
 26         step = c;
 27         gb = d;
 28     }
 29 };
 30 
 31 void init(){
 32     cin>>ss;
 33     int tem = ss;
 34     for(int i=5;i>=0;i--){
 35         s[i]=tem%10;tem/=10;
 36     }
 37     cin>>tt;
 38     tem = tt;
 39     for(int i=5;i>=0;i--){
 40         t[i]=tem%10;tem/=10;
 41     }
 42     memset(vis,false,sizeof vis);
 43 }
 44 
 45 int bfs(){
 46     queue<node> q;
 47     vis[ss][0]=true;
 48     q.push(node(s,0,0));
 49     while(!q.empty()){
 50         node p = q.front();q.pop();
 51         int nn = getNum(p.a);
 52         if(nn==tt) return p.step;
 53         //swag0--------------------
 54         if(p.gb!=0){
 55             node u = p;
 56             int sw = u.a[0] ;u.a[0] = u.a[p.gb] , u.a[p.gb] = sw;
 57             sw = getNum(u.a);
 58             if(!vis[sw][p.gb]){
 59             vis[sw][p.gb] = true;
 60                 u.step++;
 61                 q.push(u);
 62             }
 63         }
 64         //swag1--------------------
 65         if(p.gb!=5){
 66             node u = p;
 67             int sw = u.a[5] ;u.a[5] = u.a[p.gb] , u.a[p.gb] = sw;
 68             sw = getNum(u.a);
 69             if(!vis[sw][p.gb]){
 70                 vis[sw][p.gb] = true;
 71                 u.step++;
 72                 q.push(u);
 73             }
 74         }
 75         //up------------------------------
 76         if(p.a[p.gb]!=9&&p.a[p.gb]!=t[p.gb]){
 77             node u = p;
 78             u.a[p.gb]++;
 79             int sw = getNum(u.a);
 80             if(!vis[sw][p.gb]){
 81                 vis[sw][p.gb] = true;
 82                 u.step++;
 83                 q.push(u);
 84             }
 85         }
 86         //down------------------------------
 87         if(p.a[p.gb]!=0&&p.a[p.gb]!=t[p.gb]){
 88             node u = p;
 89             u.a[p.gb]--;
 90             int sw = getNum(u.a);
 91             if(!vis[sw][p.gb]){
 92                 vis[sw][p.gb] = true;
 93                 u.step++;
 94                 q.push(u);
 95             }
 96         }
 97         //left-----------------------
 98         if(p.gb!=0&&(p.a[p.gb]==t[p.gb]||p.gb==5)&&!vis[nn][p.gb-1]){
 99                 vis[nn][p.gb-1] = true;
100                 q.push(node(p.a,p.step+1,p.gb-1));
101         }
102         //right-----------------------
103         if(p.gb!=5&&(p.a[p.gb]==t[p.gb]||p.gb==0)&&!vis[nn][p.gb+1]){
104                 vis[nn][p.gb+1] = true;
105                 q.push(node(p.a,p.step+1,p.gb+1));
106         }
107     }
108     return -1;
109 }
110 
111 int main()
112 {
113     init();
114     cout<<bfs()<<endl;
115     return 0;
116 }

View Code

Paint on a WallHDU - 4012

题意：给你一个最大2*8的画图板，一次只能上色一个长方形（正方形也是长方形的一种），新的颜色会覆盖旧的颜色，问要最少上色多少次可以变成目标颜色。

算法：BFS+位压缩

思路：总要的是说三遍：和颜色无关！和颜色无关！和颜色无关！

　　　因为你每一次上色都必须留下一个最终颜色块，不然你的上色就是无效操作，即每次操作至少会产生一个目标颜色块。

　　　用1<<16的数来记录方格是否达到目标色块，然后BFS每一次都在没有达到目标色块的方格上，进行长方形扩展，寻找达到目标色块的方格记录入队就行了。

　　　参考大神博客：https://blog.csdn.net/hexianhao/article/details/50791187

　　　想了很久，终于想明白了，单行可以不向左扩展，因为都是从左到右把颜色判断过了。双行必须向左扩展，因为我们都是以上面的颜色判断，但是下面的目标颜色可能会出现在前面，所以需要向前扩展寻找。

扩展知识：for(int j=tmp;j>0;j=tmp&(j-1) 这里循环列举 tmp 所有子集合。位运算小知识

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 
 9 using namespace std;
10 
11 const int INF = 0x3f3f3f3f;
12 
13 int n;
14 bool vis[1<<16];
15 char ditu[17];
16 
17 struct node{
18     int s,step;
19     node(int ss,int stepp):s(ss),step(stepp) {};
20     bool check(){
21         return s==((1<<2*n)-1) ;
22     }
23 };
24 
25 int bfs(){
26     memset(vis,false,sizeof vis);
27     queue<node> q;
28     vis[0]=true;
29     q.push(node(0,0));
30     while(!q.empty()){
31         node p = q.front();q.pop();
32         if(p.check()) return p.step;
33         for(int i=0;i<2*n;i++){
34             if(p.s&(1<<i)) continue;
35             int tmp=0;
36             for(int j=i;j<(i/n+1)*n;j++){
37                 if(p.s&(1<<j)) break;
38                 if(ditu[i]==ditu[j]) tmp|=(1<<j);
39             }
40             for(int j=tmp;j>0;j=tmp&(j-1)){
41                 if(vis[j|p.s]) continue;
42                 vis[j|p.s]=true;
43                 q.push(node(j|p.s,p.step+1));
44             }
45             if(i>=n||p.s&(1<<i+n)) continue;
46             tmp=0;
47             for(int j=i;j<n;j++){
48                 if(p.s&(1<<j)||p.s&(1<<j+n)) break;
49                 if(ditu[i]==ditu[j]) tmp|=(1<<j);
50                 if(ditu[i]==ditu[j+n]) tmp|=(1<<j+n);
51             }
52             for(int j=i-1;j>=0;j--){
53                 if(p.s&(1<<j)||p.s&(1<<j+n)) break;
54                 if(ditu[i]==ditu[j+n]) tmp|=(1<<j+n);
55             }
56             for(int j=tmp;j>0;j=tmp&(j-1)){
57                 if(vis[j|p.s]) continue;
58                 vis[j|p.s]=true;
59                 q.push(node(j|p.s,p.step+1));
60             }
61         }
62     }
63 }
64 
65 void init(){
66     cin>>n;
67     for(int i=0;i<2*n;i++){
68         char ch=getchar();while(ch==' '||ch=='\n') ch=getchar();
69         ditu[i]=ch;
70     }
71     //cout<<((1<<2*n)-1) <<endl;
72     //for(int i=0;i<2*n;i++) cout<<ditu[i]<<" ";cout<<endl;
73 }
74 
75 int main()
76 {
77     int cas;cin>>cas;
78     for(int i=1;i<=cas;i++){
79         init();
80         cout<<"Case #"<<i<<": "<<bfs()<<endl;
81     }
82     return 0;
83 }

View Code

Knight's TripHDU - 3766

题意：马走日，一开始坐标（0,0），给你一个目标（x,y）,问你走到这个目标最少要多少步？棋盘坐标最大上下正负百万

算法：规律题

思路：这题其实只要找一个一个界限内的答案就行了，正负改为绝对值就行了。正常预处理BFS，需要二维数组开到百万的平方，绝对会MLE。

　　　所以这题乖乖找规律就行了。

　　　最近没什么耐心....v-v....所以画图想了一下。

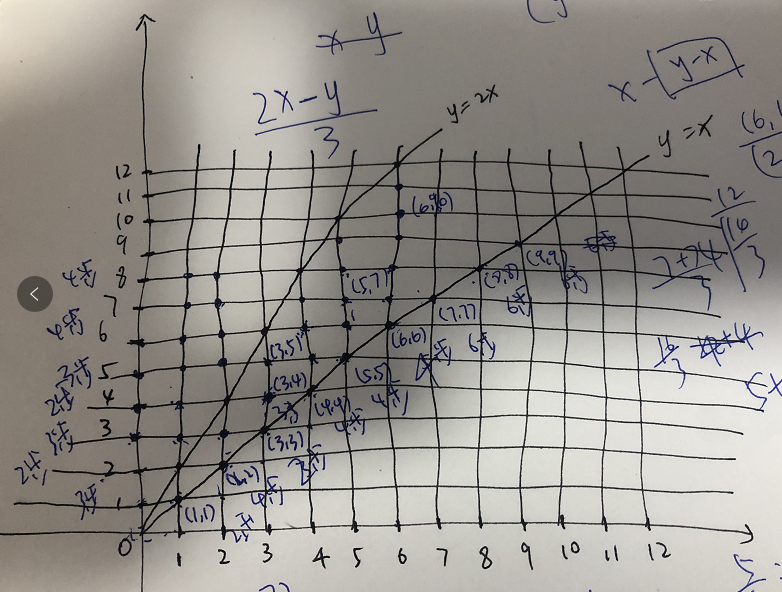
　　　分析：1.这里通过x,y负数变正只考虑第一象限，然后将x，y大小比较置换，使得只考虑x=y线的上半部分；

　　　　　　2.然后我们分三种情况：

　　　　　　　　1）先考虑y=2x,因为这条线是从（0,0）只进行（1,2）操作形成的线，所以在这条线上的答案都是x

　　　　　　　　2）考虑y>2x,这部分是在线y=2x上面的，这部分的点可以先进行（-1，-2）操作进行下降接近（0,0），然后落在y轴上————这里操作数等于x，自己验证一下；然后都到达y轴，变成了（0，y-2x），剩下的就进行（1,-2）（-1,2）交替接近（0,0）；就相当于（y-2x）/4，存在五种情况，1——落在了（0,0），答案就是（y-2x）/4; 2——然后特殊情况（0,1），这个点到（0,0）需要3步； 3——（0,5）到（0,0）也只需要3步，所以本来要落到（0,1）上面的点只要落到（0，5）就行了；4——落在了（0,2）这种2步；5——落在（0,3）3步

　　　　　　　　3）考虑y<2x，这部分也是通过（-1,-2）操作向下向左靠近（0,0），并且无一例外都掉在y=x线上，通过规律总结，下降操作数等于（y-x），会落在（2x-y,2x-y）的点上，然后y=x线上的点，到（0,0）是有规律的，除了（2,2）是特例，他是需要4步的，其他都是阶段性的递增，如图所示

易错点：这里输入我试了很多种办法都wrong了，然后学了其他博主的输入之后就ac了你们可以尝试一下

 1 #include<stdio.h>
 2 #include<string.h>
 3 
 4 int run(int x,int  y){
 5     if(x==2&&y==2) return 4;
 6     if(x==0&&y==1) return 3;
 7     if(y==2*x) return x;
 8     if(y<2*x) return y-x + (2*x-y)/3*2 + ((2*x-y)%3?2:0);
 9     return (y-2*x)/4*2+(y-2*x)%4+x;
10 }
11 
12 int main()
13 {
14     char c[20];
15     while(scanf("%s", c), strcmp(c, "END"))
16     {
17         int x, y;
18         int k;
19         sscanf(c, "%d", &x);
20         scanf("%d", &y);
21         if(x<0) x = -x;
22         if(y<0) y = -y;
23         if(y<x) {k=x, x=y, y=k;}
24         printf("%d\n", run(x,y));
25     }
26     return 0;
27 }

View Code

SnakeHDU - 2605

题意：一条蛇在吃豆子，吃完豆子就会消失，且蛇身体不会变长，并且豆子之间存在关系，豆子必须在它的唯一关键豆子被吃掉的情况下才能被吃。蛇不能穿过自己的身体。

算法：状态压缩+BFS+剪枝

思路：和上面的题 Holedox MovingPOJ - 1324 思路一样。

　　　判重，一开始我的想法是，vis[x][y][吃豆子状态][蛇身体状态]，然后不出意外MLE了。后面我改用DFS，就TLE。然后尝试用DFS枚举所有吃豆子情况，然后每次吃豆子用Astar求最短路径，WrongAnser，所以这里中间吃豆子，最快并不是最优，因为存在蛇身状态的影响。

　　　实在没办法，求助我的大学同学（大牛），然后他在我软磨硬泡之下，尝试了几次，后面被他AC了。他的思路就是，维护一个三维vis[x][y][吃豆子状态]最优，蛇身体状态则用其他思路弥补。

他的代码：

import java.io.IOException;
import java.io.InputStream;
import java.util.*;

public class Main {
    private static final FastReader cin = new FastReader(System.in);

    private static final int N = 21;
    private static final int ST = 1 << 7;
    private static final int WALL = 1;
    private static final int BEAN = 2;
    private static final int UNKNOWN = 4;
    private static final int HAS_BEAN_CAN_NOT_EAT = 5;
    private static final int HAS_BEAN_AND_EAT = 6;

    private static int H, W, L, K, R, n;
    private static final int[] key = new int[N * N];
    private static final int[] next = new int[N * N];
    private static final int[] beanX = new int[N];
    private static final int[] beanY = new int[N];
    private static final int[][] beanId = new int[N][N];

    private static final int[][][] beanToAnywhere = new int[8][N][N];

    private static final int[] dirX = new int[]{1, 0, 0, -1};
    private static final int[] dirY = new int[]{0, 1, -1, 0};
    private static final int[][][][] dp = new int[N][N][ST][8];

    private static void init() {
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                for (int st = 0; st < ST; ++st) {
                    for (int k = 0; k <= K; ++k) {
                        dp[i][j][st][k] = Integer.MAX_VALUE;
                    }
                }
            }
        }
        for (int b = 0; b < K; ++b) {
            for (int i = 0; i < N; ++i) {
                for (int j = 0; j < N; ++j) {
                    beanToAnywhere[b][i][j] = Integer.MAX_VALUE;
                }
            }
        }
    }

    private static void initBeanToAnywhere(int x, int y, int[][] dis, int step, int[][] map) {
        if (dis[x][y] <= step) return;
        dis[x][y] = step;
        for (int d = 0; d < 4; ++d) {
            int nx = x + dirX[d];
            int ny = y + dirY[d];
            if (nx <= 0 || ny <= 0 || nx > H || ny > W) continue;
            if (map[nx][ny] == WALL) continue;
            initBeanToAnywhere(nx, ny, dis, step + 1, map);
        }
    }

    private static int encodeBody(List<Integer> bodyX, List<Integer> bodyY) {
        int[] target = new int[L];
        for (int i = 0; i < L - 1; ++i) {
            int x = bodyX.get(i);
            int y = bodyY.get(i);
            int nxtX = bodyX.get(i + 1);
            int nxtY = bodyY.get(i + 1);
            for (int d = 0; d < 4; ++d) {
                if (x + dirX[d] == nxtX && y + dirY[d] == nxtY) {
                    target[i] = d;
                    break;
                }
            }
        }
        int res = 0;
        for (int i = L - 2; i >= 0; --i) {
            res *= 4;
            res += target[i];
        }
        return res;
    }

    private static List<Integer> decode(int begin, int code, int[] dir) {
        List<Integer> res = new ArrayList<>();
        res.add(begin);
        int pre = begin;
        for (int i = 1; i < L; ++i) {
            int d = code % 4;
            code /= 4;
            int now = pre + dir[d];
            res.add(now);
            pre = now;
        }
        return res;
    }

    private static int move(int body, int d) {
        int nBody = body * 4 + (3 - d);
        int stSize = 1 << ((L - 1) * 2);
        return nBody & (stSize - 1);
    }

    private static boolean isBody(int headX, int headY, int x, int y, int code) {
        if (x == headX && y == headY) return true;
        int nowX = headX;
        int nowY = headY;
        for (int i = 1; i < L; ++i) {
            int d = code % 4;
            code /= 4;
            nowX += dirX[d];
            nowY += dirY[d];
            if (x == nowX && y == nowY) return true;
        }
        return false;
    }

    private static void checkEncode(List<Integer> bodyX, List<Integer> bodyY) {
        int code = encodeBody(bodyX, bodyY);
        List<Integer> decodeX = decode(bodyX.get(0), code, dirX);
        List<Integer> decodeY = decode(bodyY.get(0), code, dirY);

        for (int i = 0; i < L; ++i) {
            System.out.println(bodyX.get(i) + " " + bodyY.get(i) + " " + decodeX.get(i) + " " + decodeY.get(i));
//            if(!Objects.equals(decodeX.get(i), bodyX.get(i))) {System.out.println("FUCK");break;}
//            if(!Objects.equals(decodeY.get(i), bodyY.get(i))) {System.out.println("FUCK");break;}
        }
    }

    public static final class Node {
        int x;
        int y;
        int st;
        int step;
        int body;

        int lastBeanId;

        Node(int x, int y, int st, int step, int body, int lastBeanId) {
            this.x = x;
            this.y = y;
            this.st = st;
            this.step = step;
            this.body = body;
            this.lastBeanId = lastBeanId;
        }

        public void show() {
            System.out.print(x + " " + y + " " + showSt(st) + " " + step + " " + showSt(body) + " (");
            List<Integer> nxs = decodeBody(x, body, dirX);
            List<Integer> nys = decodeBody(y, body, dirY);
            for (int i = 0; i < L; ++i) System.out.print(nxs.get(i) + " " + nys.get(i) + ",");
            System.out.println(")");
        }

        public long hash() {
            long res = 0;
            res |= body;

            // step 2800以内
            res <<= 12;
            res |= step;

            // 吃豆状态
            res <<= 7;
            res |= st;

            // 位置 400 以内
            res <<= 9;
            res |= ((long) (x - 1) * W + y - 1);

            res <<= 3;
            res |= lastBeanId;

            return res;
        }

        public static Node decode(long code) {
            int lastBeanId = (int) (code & ((1L << 3) - 1));
            code >>= 3;

            int posCode = (int) (code & ((1L << 9) - 1));
            int x = (posCode / W) + 1;
            int y = (posCode % W) + 1;
            code >>= 9;

            int st = (int) (code & ((1L << 7) - 1));
            code >>= 7;

            int step = (int) (code & ((1L << 12) - 1));
            code >>= 12;

            int body = (int) code;
            return new Node(x, y, st, step, body, lastBeanId);
        }

        public int countSt() {
            int res = 0;
            for (int i = 0; i < 7; ++i) {
                if ((st & (1 << i)) > 0) res++;
            }
            return res;
        }
    }


    private static List<Integer> decodeBody(int begin, int code, int[] dir) {
        List<Integer> res = new ArrayList<>();
        res.add(begin);
        int pre = begin;
        for (int i = 1; i < L; ++i) {
            int d = code % 4;
            code /= 4;
            int now = pre + dir[d];
            res.add(now);
            pre = now;
        }
        return res;
    }


    private static int bfs(int x, int y, int body, int[][] map) {
        Queue<Long> queue = new LinkedList<>();
        Node start = new Node(x, y, 0, 0, body, 0);
        queue.add(start.hash());
        dp[x][y][0][0] = 0;
        int maxSize = 0;
        while (!queue.isEmpty()) {
            maxSize = Math.max(maxSize, queue.size());
            Node top = Node.decode(queue.poll());
            if (top.st == (1 << K) - 1) {
//                System.out.println(maxSize);
                return top.step;
            }
            if (top.step > H * W * (top.countSt() + 1)) continue;
//            if (top.step - 2 > dp[top.x][top.y][top.st]) continue;
//            if (top.x == 3 && top.y == 7)
//                top.show();

            for (int d = 0; d < 4; ++d) {
                int nx = top.x + dirX[d];
                int ny = top.y + dirY[d];
                int nSt = top.st;
                int nLastBeanId = top.lastBeanId;
                if (nx <= 0 || ny <= 0 || nx > H || ny > W) continue;

                int now = map[nx][ny];
                if (now == WALL) continue;
                if (isBody(top.x, top.y, nx, ny, top.body)) continue;

                int eat = UNKNOWN;
                if (now == BEAN) {
                    int id = beanId[nx][ny];
                    for (int i = 0; i < R; ++i) {
                        if (next[i] == id && (((1 << key[i]) & top.st) == 0)) {
                            eat = HAS_BEAN_CAN_NOT_EAT;
                            break;
                        }
                    }
                    if (eat == UNKNOWN) {
                        eat = HAS_BEAN_AND_EAT;
                        nSt = top.st | (1 << id);
                        nLastBeanId = id;
                    }
                }

                if (eat == HAS_BEAN_CAN_NOT_EAT) continue;
                int nStep = top.step + 1;
                boolean go = false;
                if (nStep < dp[nx][ny][nSt][nLastBeanId]) {
                    dp[nx][ny][nSt][nLastBeanId] = nStep;
                    go = true;
                }

                // 吃过豆, 并且上一个豆到当前点距离
                int nowMinDis = dp[nx][ny][nSt][nLastBeanId];
                int preToNowDis = beanToAnywhere[top.lastBeanId][nx][ny];
                if (top.st != 0 &&  nStep < nowMinDis + L && preToNowDis < L) {
                    go = true;
                }

                if (go) {
                    int nBody = move(top.body, d);
                    queue.add(new Node(nx, ny, nSt, nStep, nBody, nLastBeanId).hash());
                }
            }
        }
        return Integer.MAX_VALUE;
    }

    /**
     * 入度判断环
     */
    private static boolean checkCircle() {
        int[] in = new int[K];
        for (int i = 0; i < R; ++i) {
            in[next[i]]++;
        }
        Queue<Integer> root = new LinkedList<>();
        for (int i = 0; i < K; ++i) {
            if (in[i] == 0) root.add(i);
        }
        while (!root.isEmpty()) {
            int nowRoot = root.poll();
            for (int i = 0; i < R; ++i) {
                if (key[i] == nowRoot) {
                    in[next[i]]--;
                    if (in[next[i]] == 0) root.add(next[i]);
                }
            }
        }
        for (int i = 0; i < K; ++i)
            if (in[i] > 0) {
                return true;
            }
        return false;
    }

    /**
     * 判断可达
     */
    private static void checkReach(int x, int y, int[][] map, boolean[][] vis) {
        if (vis[x][y]) return;
        vis[x][y] = true;
        for (int d = 0; d < 4; ++d) {
            int nx = x + dirX[d];
            int ny = y + dirY[d];
            if (nx <= 0 || ny <= 0 || nx > H || ny > W) continue;
            if (map[nx][ny] == WALL) continue;
            checkReach(nx, ny, map, vis);
        }
    }

    private static void solve() {

        H = cin.nextInt();
        W = cin.nextInt();
        L = cin.nextInt();
        K = cin.nextInt();
        R = cin.nextInt();
        n = cin.nextInt();

        int[][] map = new int[21][21];

        List<Integer> bodyX = new ArrayList<>();
        List<Integer> bodyY = new ArrayList<>();

        for (int i = 0; i < L; ++i) {
            int x = cin.nextInt();
            int y = cin.nextInt();
            bodyX.add(x);
            bodyY.add(y);
        }

        for (int i = 0; i < K; ++i) {
            int x = cin.nextInt();
            int y = cin.nextInt();
            beanX[i] = x;
            beanY[i] = y;
            map[x][y] = BEAN;
            beanId[x][y] = i;
        }

        for (int i = 0; i < R; ++i) {
            key[i] = cin.nextInt() - 1;
            next[i] = cin.nextInt() - 1;
        }

        for (int i = 0; i < n; ++i) {
            int x = cin.nextInt();
            int y = cin.nextInt();
            map[x][y] = WALL;
        }

        init();

        if (checkCircle()) {
            System.out.println(-1);
            return;
        }

        // 判断可达
        boolean[][] vis = new boolean[21][21];
        checkReach(bodyX.get(0), bodyY.get(0), map, vis);
        // 预处理豆到地图任一点距离
        for (int i = 0; i < K; ++i) {
            initBeanToAnywhere(beanX[i], beanY[i], beanToAnywhere[i], 0, map);
        }

        for (int i = 0; i < K; ++i) {
            if (!vis[beanX[i]][beanY[i]]) {
                System.out.println(-1);
                return;
            }
        }

        int code = encodeBody(bodyX, bodyY);

        int ans = bfs(bodyX.get(0), bodyY.get(0), code, map);

        System.out.println(ans == Integer.MAX_VALUE ? -1 : ans);
    }


    public static void main(String[] args) {
        int t = cin.nextInt();
        for (int tt = 0; tt < t; ++tt) solve();
    }


    /**
     * 打印状态压缩
     */
    private static String showSt(int st) {
        StringBuilder res = new StringBuilder();
        for (int i = 0; i < 2 * L; ++i) {
            if ((st & (1 << i)) == 0) res.append("0");
            else res.append("1");
        }
        return res.toString();
    }

    private static class FastReader {
        private InputStream stream;

        private byte[] buf = new byte[1024];

        private int curChar;

        private int numChars;

        FastReader(InputStream stream) {
            this.stream = stream;
        }

        int read() {
            if (numChars == -1) {
                throw new InputMismatchException();
            }
            if (curChar >= numChars) {
                curChar = 0;
                try {
                    numChars = stream.read(buf);
                } catch (IOException e) {
                    throw new InputMismatchException();
                }
                if (numChars <= 0) {
                    return -1;
                }
            }
            return buf[curChar++];
        }

        int nextInt() {
            int c = read();
            while (isSpaceChar(c)) {
                c = read();
            }
            int sgn = 1;
            if (c == '-') {
                sgn = -1;
                c = read();
            }
            int res = 0;
            do {
                if (c < '0' || c > '9') {
                    throw new InputMismatchException();
                }
                res *= 10;
                res += c - '0';
                c = read();
            } while (!isSpaceChar(c));
            return res * sgn;
        }

        public long nextLong() {
            long ret = 0;
            int c = read();
            while (c <= ' ') {
                c = read();
            }
            boolean neg = (c == '-');
            if (neg) {
                c = read();
            }
            do {
                ret = ret * 10 + c - '0';
            } while ((c = read()) >= '0' && c <= '9');
            if (neg) {
                return -ret;
            }
            return ret;
        }

        public String next() {
            int c = read();
            while (isSpaceChar(c)) {
                c = read();
            }
            StringBuilder res = new StringBuilder();
            do {
                res.appendCodePoint(c);
                c = read();
            } while (!isSpaceChar(c));
            return res.toString();
        }

        boolean isSpaceChar(int c) {
            return c == ' ' || c == '\n' || c == '\r' || c == '\t' || c == -1;
        }
    }
}

View Code

　　　我看了他的代码，以下是我的理解：

　　　存在一个情况，就是他不是吃到豆子最快，但是因为他的吃豆子蛇的状态，导致他到下一个豆子的后续步数优于最快吃到豆子的状况；所以只要步数不多于最快吃到豆子的最坏情况下，都可以入队进行角逐答案。

　　 1.蛇身体之所以可以影响答案，在于蛇身会阻碍蛇某个方向前进，所以如果蛇可以掉头了，他所有方向都可以去了

　　　2.理想情况下，蛇只需要走蛇身步数就可以掉头

　　　3.为了减少存储，所以只让蛇在豆子蛇身范围内进行掉头，所有其他位置蛇只要前进就行了。

　　　4.这里理想情况下，蛇在最快吃到豆子之后，蛇身步数，离豆子蛇身范围内可以变换成任何形态(存在石头阻碍情况下，无法实现，但是测试数据没有)

　　 5.如果你在最优情况外，在豆子附件蛇身范围内，小于蛇身步数，皆可入队，这里就是考虑到其他蛇身状态下，对最终答案的影响。

易错点：这里豆子会成环，导致成环豆子都无法被吃；然后这里为了节省空间，将node的所有东西压缩到一个longlong里面。

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <map>

using namespace std;

const int INF = 0x3f3f3f3f;

int H,W,snakeNum,beanNum,R,stNum;
int snakeHeadX,snakeHeadY,snakeBody;
int ditu[21][21];
int dis[8][21][21];//预处理每个豆子到各点距离
int vis[21][21][1<<7];//三维 坐标+吃豆子状态
int xx[] = {0,1,0,-1};
int yy[] = {1,0,-1,0};

//豆子坐标 + 关键豆子ID
struct bean{
    int x,y,key;
    bean() {}
    bean(int a,int b,int c):x(a),y(b),key(c) {}
}beans[8];


//预处理标记每个豆子蛇身长度范围内可达的点-----------------
struct tmtp{
    int x,y;
    tmtp(int a,int b):x(a),y(b) {};
};
void BFSFB(int b){
    dis[b][beans[b-1].x][beans[b-1].y]=0;
    queue<tmtp> q;
    q.push(tmtp(beans[b-1].x,beans[b-1].y));
    while(!q.empty()){
        tmtp p = q.front();q.pop();
        if(dis[b][p.x][p.y]>=snakeNum) continue;
        for(int i=0;i<4;i++){
            int x = p.x + xx[i] , y = p.y +yy[i];
            if(x<=0||x>H||y<=0||y>W||ditu[x][y]==-2) continue;
            if(dis[b][x][y]<=dis[b][p.x][p.y]+1) continue;
            dis[b][x][y]=dis[b][p.x][p.y]+1;
            q.push(tmtp(x,y));
        }
    }
}

//各种输入和预处理-----------------------------------------
void init(){
    cin>>H>>W>>snakeNum>>beanNum>>R>>stNum;
    cin>>snakeHeadX>>snakeHeadY;
    int a=snakeHeadX,b=snakeHeadY,c,d;
    snakeBody=0;
    for(int i=0;i<snakeNum-1;i++){
        cin>>c>>d;
        snakeBody<<=2;
        if(c-a==0&&d-b==1) snakeBody+=0;
        else if(c-a==1&&d-b==0) snakeBody+=1;
        else if(c-a==0&&d-b==-1) snakeBody+=2;
        else if(c-a==-1&&d-b==0) snakeBody+=3;
        a=c,b=d;
    }
    memset(ditu,-1,sizeof ditu);
    for(int i=0;i<beanNum;i++){
        cin>>a>>b;
        ditu[a][b]=i;
        beans[i].x=a,beans[i].y=b;beans[i].key=-1;
    }
    for(int i=0;i<R;i++){
        cin>>a>>b;
        beans[b-1].key=a-1;
    }
    for(int i=0;i<stNum;i++){
        cin>>a>>b;
        ditu[a][b]=-2;
    }
    memset(dis,INF,sizeof dis);
    for(int i=0;i<beanNum;i++){
        BFSFB(i+1);
    }
}

//有一个状态压缩函数和一个状态解压函数-----------------------
struct node{
    int x,y,snake,state,lastBeanId,step;
    node(int a,int b,int c,int d,int e,int f):x(a),y(b),snake(c),state(d),lastBeanId(e),step(f) {}
    node(long long tmt){
        lastBeanId = (int) (tmt % (1L<<4));
        tmt = tmt >>4;
        step = (int) (tmt % (1L<<12));
        tmt = tmt >>12;
        state =(int) ( tmt % (1L<<7));
        tmt = tmt>>7;
        snake = (int) (tmt % (1L<<14));
        tmt = tmt>>14;
        y = (int) (tmt % 21),x = (int) (tmt / 21);
    }
    long long makeHash(){
        long long  ans = x*21+y;
        ans <<= 14;ans += snake;
        ans <<= 7;ans += state;
        ans <<= 12;ans+=step;
        ans <<= 4;ans+=lastBeanId;
        return ans;
    }
};

//判断是否碰到蛇身------------------------------------
bool checkXY(int Sx,int Sy,int snake,int tx,int ty){
    int w = (1<<((snakeNum-2)*2));
    int t = snakeNum-1;
    while(t--){
        int tmp = (snake / w)%4;
        Sx+=xx[tmp],Sy+=yy[tmp];
        if(Sx==tx&&Sy==ty) return true;
        w>>=2;
    }
    return false;
}

//答案搜索----------------------------------
int BFS(){
    queue<long long> q;
    memset(vis,INF,sizeof vis);
    vis[snakeHeadX][snakeHeadY][0]=0;
    node start = node(snakeHeadX,snakeHeadY,snakeBody,0,0,0);
    long long tnt = start.makeHash();
    q.push(tnt);

    while(!q.empty()){
        long long pNum = q.front();q.pop();
        node p = node(pNum);

        if((1<<beanNum)-1 == p.state) return p.step;
        if(p.step>H*W*beanNum) continue;

        for(int i=0;i<4;i++){

            int x = p.x + xx[i] , y = p.y +yy[i];
            if(x<=0||x>H||y<=0||y>W||ditu[x][y]==-2) continue;
            if( ditu[x][y] != -1 && beans[ditu[x][y]].key != -1&&((1<<beans[ditu[x][y]].key)&p.state)==0) continue;
            if(checkXY(p.x,p.y,p.snake,x,y)) continue;

            int state = p.state, lastBeanId = p.lastBeanId;
            if(ditu[x][y] != -1&&((1<<ditu[x][y])&p.state)==0) {state |= (1<<ditu[x][y]);lastBeanId = ditu[x][y] +1;}

            bool flag = true;
            //维护步数最优------------------------------
            //这里如果开思维，加上蛇的身体，1<<14-----就会MLE----------------
            if(vis[x][y][state]>p.step+1) {
                vis[x][y][state]=p.step+1;
                flag = false;
            }
            //蛇身体之所以可以影响答案，在于蛇身会阻碍蛇某个方向前进，所以如果蛇可以掉头了，他所有方向都可以去了
            //理想情况下，蛇只需要走蛇身步数就可以掉头
            //为了减少存储，所以只让蛇在豆子蛇身范围内进行掉头
            //这里理想情况下，蛇在最快吃到豆子之后，蛇身步数，离豆子蛇身范围内可以变换成任何形态(存在石头阻碍情况下，无法实现，但是测试数据没有)
            if(state!=0&&(p.step+1<vis[x][y][state]+snakeNum)&&dis[lastBeanId][x][y]<snakeNum) flag = false;
            if(flag) continue;

            int body = p.snake >>2 ;
            if(i==0) body+=(2<<((snakeNum-2)*2));
            else if(i==1) body+=(3<<((snakeNum-2)*2));
            else if(i==2) body+=(0<<((snakeNum-2)*2));
            else body += (1<<((snakeNum-2)*2));

            node tmp = node(x,y,body,state,lastBeanId,p.step+1);
            long long tnt = tmp.makeHash();
            q.push(tnt);
        }
    }
    return -1;
}

//判断豆子是否成环
bool vis2[8];
bool ok(int x){
    vis2[x]=true;
    int key = beans[x].key;
    if(key==-1) return false;
    if(vis2[key]) return true;
    return ok(key);
}

int main()
{
    int _;cin>>_;
    while(_--){
        init();
        bool flag = false;
        for(int i=0;i<beanNum;i++){
            memset(vis2,false,sizeof vis2);
            if(ok(i)) {flag=true;break;}
        }
        if(flag) puts("-1");
        else cout<<BFS()<<endl;
    }
    return 0;
}

View Code

FreeOpenHDU - 3121

题意：给你男生女生宠物进行配对，条件：男生和女生必须相互喜欢并且他们也要同时喜欢同一个宠物；（男生、女生、宠物只能配对一次）求最大能配对多少对？

算法:二分最大匹配+IDAstar

思路：一开始看到这题，就想到二分最大匹配；然后这里是三分图，所以就想到最大流；但是经典三分图匹配，是中间点拆分，然后左右两个点集合是没有关系要求的，这题不同，他们三方都互相牵制；女生和男生要互相喜欢，男生和女生要喜欢同一只宠物。

　　　然后我就开始找三分图最大匹配看，有没有其他解决办法。然后百度到一个人问到类似的问题https://ask.csdn.net/questions/7763032

　　如上图所示，如果员工只要吃到喜欢的盒饭和饮料就行，只要将员工在中间拆点，然后最大流就可以解决。但是存在员工只喜欢特定的盒饭搭配，比如吃盒饭2只配饮料5、吃盒饭3只配饮料4。

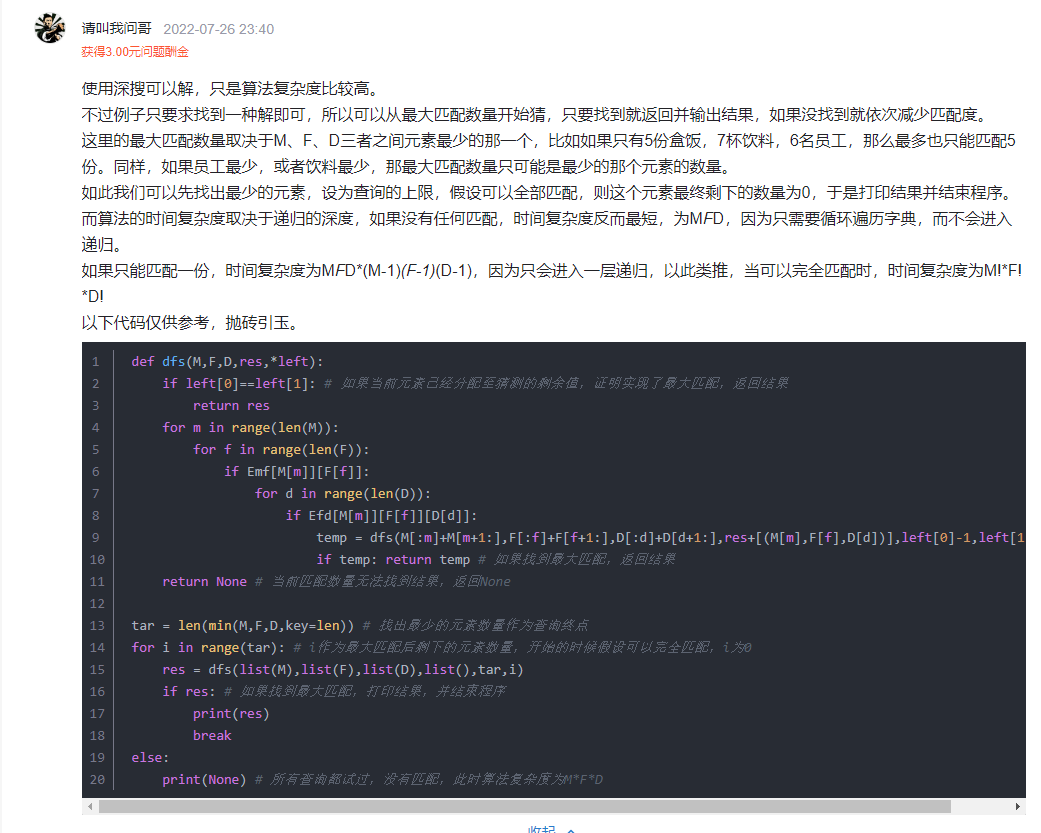
　　这个回答，让我找到了方向，立马按他的想法，进行dfs深搜，然后不出意外，TLE了。

　　实在想不到办法的我，看了别人的博客，https://blog.csdn.net/weixin_30610755/article/details/94995863

　　他的思路就是，使用IDAstar算法，limit由三个集合最小量开始，逐1递减。启发判断函数，通过三次二分图最大匹配（女男、女宠、男宠）预估接下来的最大匹配数，如果其中一个求出的最大匹配加上　　　　　　步数小于limit则跳出，让limit-=1；答案最大匹配数一定小于三个二分最大匹配的最小值，所以如果其中一个小于limit，表示当前limit不成立，不需要往下深搜了。

易错点：就算用上博主的IDAstar算法，还是容易TLE，然后我照着博主代码慢慢改自己的，然后在一个判断上，我把他分成两份了，但是其实合在一起一次判断会更快一点。

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <map>

using namespace std;

const int INF = 0x3f3f3f3f;

int g,b,p,G,B,P;
int gb[21],gp[21],bp[21];
int gg[21],gr[21];
int ans;

bool cmp(const int &a,const int &b){
    return gr[a] < gr[b];
}

void init(){
    cin>>g>>b>>p;
    ans = min(g,b);ans = min(ans,p);
    G=0,B=0,P=0;
    memset(gb,0,sizeof gb);
    for(int i=0;i<g;i++){
        for(int j=0;j<b;j++){
            int t;cin>>t;
            if(t) gb[i] |= (1<<j);
        }
    }
    memset(gp,0,sizeof gp);
    for(int i=0;i<g;i++){
        for(int j=0;j<p;j++){
            int t;cin>>t;
            if(t) gp[i] |= (1<<j);
        }
    }
    memset(bp,0,sizeof bp);
    for(int i=0;i<b;i++){
        for(int j=0;j<p;j++){
            int t;cin>>t;
            if(t) bp[i] |= (1<<j);
        }
    }
    memset(gr,0,sizeof gr);
    for(int i=0;i<g;i++){
        gg[i]=i;
        for(int j=0;j<b;j++)if(gb[i]&(1<<j)){
            if(!(gp[i]&bp[j])) gb[i]^=(1<<j);
            else gr[i]++;
        }
    }
    sort(gg,gg+g,cmp);
}

int linker[21];
int vis;

bool dfsFGB(int u){
    for(int v=0;v<b;v++){
        if(B&(1<<v)) continue;
        if(vis&(1<<v)) continue;
        if(!(gb[u]&(1<<v))) continue;
        vis |= (1<<v);
        if(linker[v] ==-1 || dfsFGB(linker[v])){
            linker[v]=u;return true;
        }
    }
    return false;
}

bool dfsFGP(int u){
    for(int v=0;v<p;v++){
        if(P&(1<<v)) continue;
        if(vis&(1<<v)) continue;
        if(!(gp[u]&(1<<v))) continue;
        vis |= (1<<v);
        if(linker[v] ==-1 || dfsFGP(linker[v])){
            linker[v]=u;return true;
        }
    }
    return false;
}

bool dfsFBP(int u){
    for(int v=0;v<p;v++){
        if(P&(1<<v)) continue;
        if(vis&(1<<v)) continue;
        if(!(bp[u]&(1<<v))) continue;
        vis |= (1<<v);
        if(linker[v] ==-1 || dfsFBP(linker[v])){
            linker[v]=u;return true;
        }
    }
    return false;
}

bool forLimit(int step,int gN){
    int res = 0;
    memset(linker,-1,sizeof linker);
    for(int u=gN;u<g;u++){
        vis=0;
        if(dfsFGB(gg[u])) res++;
        if(res+step>=ans) break;
    }
    if(res+step<ans) return true;

    res = 0;
    memset(linker,-1,sizeof linker);
    for(int u=gN;u<g;u++){
        vis=0;
        if(dfsFGP(gg[u])) res++;
        if(res+step>=ans) break;
    }
    if(res+step<ans) return true;

    res = 0;
    memset(linker,-1,sizeof linker);
    for(int u=0;u<b;u++){
        if(B&(1<<u)) continue;
        vis=0;
        if(dfsFBP(u)) res++;
        if(res+step>=ans) break;
    }
    if(res+step<ans) return true;

    return false;
}

bool IDAstar(int step,int gN){
    if(g-gN+step<ans) return false;
    if(step==ans) return true;
    if(forLimit(step,gN)) return false;
    for(int ii=gN;ii<g;ii++){
        int i = gg[ii];
        G |= (1<<i);
        for(int j=0;j<b;j++){
            if(B&(1<<j)) continue;
            if(!(gb[i]&(1<<j))) continue;
            B |= (1<<j);
            for(int z=0;z<p;z++){
                if(P&(1<<z)) continue;
                if(gp[i]&bp[j]&(1<<z)){
                    P |= (1<<z);
                    if(IDAstar(step+1,ii+1)) return true;
                    P ^= (1<<z);
                }
            }
            B ^= (1<<j);
        }
        G ^= (1<<i);
    }
    return false;
}

int main()
{
    int _;cin>>_;
    while(_--){
            init();
            while(1){
                if(IDAstar(0,0)) break;
                if(--ans==0) break;
            }
            cout<<ans<<endl;
    }
    return 0;
}

View Code

Unblock MeHDU - 3900

题意：关羽走华容道小游戏，地图固定6*6，然后只有竖的和横的矩形，面积只有2或者3，竖的只能竖着走，横着只能横着走，不能重叠。

算法：状压+bfs

思路：一个矩形，只需要记录一个横竖状态、一个固定行走的行或者列、一个长度、和一个偏移量（只有这个变量是改变的，偏移量在0~4或者0~3之间，我这里是左上角坐标）。然后判重，就是直接记录地图信息，其实这里只要将偏移量压缩到一个longlong里面就行了，因为偏移量在0~4或者0~3之间，所以只要开3位记录当个矩形，这里6*6/2=18（个），最多18个矩形，18*3=54位，所以开个longlong够了。

易错点：判断是否可行，这里，分两部分，竖的就是上下、横的就是左右，判断同类型矩形是否挡道，然后不同类型是否交叉；然后就是判断是否得出答案，这里记得加一，因为要划出去。

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>
#include <map>
#include <set>

using namespace std;

#define LL long long

const int INF = 0x3f3f3f3f;

int n,red;
LL s;

struct node{
    bool type;//true:竖的
    int pos,len;
    node() {};
    node(bool a,int b,int c):type(a),pos(b),len(c) {};
}blocks[19];

void init(){
    s = 0;
    for(int i=0;i<n;i++){
        int a,b,c,d,e;cin>>a>>b>>c>>d>>e;
        if(b==d){
            blocks[a] = node(true,b,e-c);
            s |= (LL)c<<a*3;
        }else{
            blocks[a] = node(false,c,d-b);
            s |= (LL)b<<a*3;
        }
    }
    cin>>red;
}

int cal(LL s,int id){
    return (int)((s&(7LL<<id*3))>>id*3);
}

bool getAns(LL s){
    int rl = cal(s,red),rr = rl + blocks[red].len;
    for(int i=0;i<n;i++){
        if(i==red) continue;
        int il = cal(s,i) , ir = il + blocks[i].len;
        if(!blocks[i].type&&blocks[i].pos==2&&il>rr) return false;
        if(!blocks[i].type) continue;
        if(blocks[i].pos<=rr) continue;
        if(il>2||ir<2) continue;
        return false;
    }
    return true;
}

bool check(LL s,int id,int ll,int rr){
    for(int i=0;i<n;i++){
        if(i==id) continue;
        int il = cal(s,i) , ir = il + blocks[i].len;
        if(blocks[i].type==blocks[id].type){
            if(blocks[i].pos!=blocks[id].pos) continue;
            if(il>rr||ir<ll) continue;
            return true;
        }else if(ll<=blocks[i].pos&&rr>=blocks[i].pos&&il<=blocks[id].pos&&ir>=blocks[id].pos) return true;
    }
    return false;
}

LL change(LL s,int id,int l){
    return s&(~(7LL<<3*id))|((LL)l<<3*id);
}

int BFS(){

    queue<pair<LL,int>> q;
    set<LL> st;
    st.insert(s);
    q.push(make_pair(s,0));

    while(!q.empty()){

        LL p = q.front().first;
        int step = q.front().second;
        q.pop();

        if(getAns(p)) return step+1;

        for(int i=0;i<n;i++){
            int il = cal(p,i) , ir = il + blocks[i].len;
            //向左或者向上
            for(int j=il-1;j>=0;j--){
                if(check(p,i,j,j+blocks[i].len)) break;
                LL u = change(p,i,j);
                if(st.find(u)!=st.end()) continue;
                st.insert(u);
                q.push(make_pair(u,step+1));
            }
            //向右或者向下
            for(int j=il+1;j+blocks[i].len<=5;j++){
                if(check(p,i,j,j+blocks[i].len)) break;
                LL u = change(p,i,j);
                if(st.find(u)!=st.end()) continue;
                st.insert(u);
                q.push(make_pair(u,step+1));
            }
        }
    }
}

int main()
{
    while(cin>>n){
        init();
        cout<<BFS()<<endl;
    }
    return 0;
}

View Code

Push BoxHDU - 1732

题意：推箱子，有三个箱子和三个洞，求将箱子推到洞口的最小步数

算法：BFS

思路：判重记录人+3个箱子的坐标；

易错点：就是这里洞口人是可以走过去的，然后箱子过了洞口还能推，自己想复杂了，因为题目说人只能走空地，我就以为洞口不可以走，所以人也不可能把箱子推出洞口，看了别人代码才发现错误的。

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 #include <set>
 9 
10 using namespace std;
11 
12 #define LL long long
13 
14 const int INF = 0x3f3f3f3f;
15 
16 int n,m;
17 char ditu[8][8];
18 bool vis[8][8][8][8][8][8][8][8];
19 int xx[]={1,0,0,-1};
20 int yy[]={0,1,-1,0};
21 
22 struct node{
23     int x[4],y[4],step;
24     bool check(){
25         for(int i=0;i<3;i++){
26             if(ditu[x[i]][y[i]]!='@') return false;
27         }
28         return true;
29     }
30     void show(){
31          for(int i=0;i<4;i++) cout<<x[i]<<" "<<y[i]<<endl;
32         cout<<step<<endl;
33     }
34 }Start;
35 
36 void init(){
37     int num = 0;
38     for(int i=0;i<n;i++)
39         for(int j=0;j<m;j++){
40             char ch=getchar();while(ch==' '||ch=='\n') ch=getchar();
41             if(ch=='X') Start.x[3] = i , Start.y[3] = j , ditu[i][j] = '.';
42             else if(ch=='*') Start.x[num] = i , Start.y[num++] = j , ditu[i][j] = '.';
43             else ditu[i][j] = ch;
44     }Start.step=0;
45 }
46 
47 int bfs(){
48     queue<node> q;
49     memset(vis,false,sizeof vis);
50     vis[Start.x[0]][Start.y[0]][Start.x[1]][Start.y[1]][Start.x[2]][Start.y[2]][Start.x[3]][Start.y[3]]=true;
51     q.push(Start);
52     while(q.size()){
53         node p = q.front();q.pop();
54         if(p.check()) return p.step;
55         for(int i=0;i<4;i++){
56             node u = p;u.step++;
57             u.x[3] += xx[i] , u.y[3] += yy[i];
58             if(u.x[3]<0||u.x[3]>=n||u.y[3]<0||u.y[3]>=m||ditu[u.x[3]][u.y[3]]=='#') continue;
59             int flag = 0;
60             for(int j=0,out = 1;j<3&&out;j++){
61                 if(u.x[j]==u.x[3]&&u.y[j]==u.y[3]){
62                     out = 0;
63                     u.x[j] += xx[i] , u.y[j] += yy[i];
64                     if(u.x[j]<0||u.x[j]>=n||u.y[j]<0||u.y[j]>=m||ditu[u.x[j]][u.y[j]]=='#') {flag=1;break;}
65                     for(int z=0;z<3;z++)if(z!=j){
66                         if(u.x[z]==u.x[j]&&u.y[z]==u.y[j]) {flag=1;break;}
67                     }
68                 }
69             }
70             if(flag) continue;
71             if(vis[u.x[0]][u.y[0]][u.x[1]][u.y[1]][u.x[2]][u.y[2]][u.x[3]][u.y[3]]) continue;
72             vis[u.x[0]][u.y[0]][u.x[1]][u.y[1]][u.x[2]][u.y[2]][u.x[3]][u.y[3]]=true;
73             q.push(u);
74         }
75     }
76     return -1;
77 }
78 
79 int main()
80 {
81     while(cin>>n>>m){
82         init();
83         cout<<bfs()<<endl;
84     }
85     return 0;
86 }

View Code

Traveling CubeHDU - 2913

题意：另一种推箱子，这种推箱子是，箱子每次都会转动。箱子每一个面都有一个颜色，六种彩色，地图上有唯一的这六种彩色地板各六个，和多个白色或者黑色的地板，箱子可以随意进出白色地板，不能进入黑色地板，进入彩色地板的条件是，进入到的时候，箱子顶上的颜色要与地板颜色一样，并且彩色地板只能进一次。而且题目会给出一个顺序，问按顺序依次进入这些彩色地板的最小步数

算法：BFS + 状压

思路：这里就是模拟题，思考上下左右转，颜色会怎么变化就好了。最主要是判重的状态压缩。我一开始直接开4维[x][y][543210][7] 直接编译不了，数组开不了那么大，后面少记录一个颜色[x][y][54321][7]，直接MLE。后面看了别人代码，写成map<LL,bool> vis[x][y][7] 就过了。

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 #include <set>
  9 
 10 using namespace std;
 11 
 12 #define LL long long
 13 
 14 const int INF = 0x3f3f3f3f;
 15 
 16 //543210 r-0 c-1 g-2 m-3 b-4 y-5
 17 int n,m,Sx,Sy;
 18 int tS[6];
 19 int ditu[31][31];//w- -1 k- -2
 20 int xx[]={0,0,-1,1};
 21 int yy[]={1,-1,0,0};
 22 
 23 struct node{
 24     int x,y,state,nowID,step;
 25     node(int a,int b,int c,int d,int e):x(a),y(b),state(c),nowID(d),step(e) {};
 26     void show(){
 27         cout<<x<<' '<<y<<' '<<state<<' '<<nowID<<' '<<step<<endl;
 28     }
 29 };
 30 
 31 int num[6];
 32 void getNum(int x){
 33     int sum = 0;
 34     for(int i=0;i<5;i++){
 35         num[i] = x %10;x/=10;
 36         sum+=num[i];
 37     }num[5] = 15 - sum;
 38 }
 39 int change(int x,int i){
 40     if(i==0) return  num[0]*10000 + num[3]*1000 + num[2]*100 + num[4]*10 + num[5];
 41     if(i==1) return  num[1]*10000 + num[3]*1000 + num[2]*100 + num[5]*10 + num[4];
 42     if(i==2) return  num[4]*10000 + num[1]*1000 + num[0]*100 + num[2]*10 + num[3];
 43     return  num[4]*10000 + num[0]*1000 + num[1]*100 + num[3]*10 + num[2];
 44 }
 45 
 46 void init(){
 47     memset(ditu,-1,sizeof ditu);
 48     for(int i=0;i<n;i++)
 49         for(int j=0;j<m;j++){
 50             char ch=getchar();while(ch=='\n'||ch==' ') ch=getchar();
 51             if(ch=='#') Sx = i,Sy = j;
 52             else if(ch=='k') ditu[i][j] = -2;else if(ch=='r') ditu[i][j] = 0;else if(ch=='c') ditu[i][j] = 1;
 53             else if(ch=='g') ditu[i][j] = 2;else if(ch=='m') ditu[i][j] = 3;else if(ch=='b') ditu[i][j] = 4;else if(ch=='y') ditu[i][j] = 5;
 54     }
 55     for(int i=0;i<6;i++){
 56         char ch=getchar();while(ch=='\n'||ch==' ') ch=getchar();
 57         if(ch=='r') tS[i] = 0;
 58         else if(ch=='c') tS[i] = 1;
 59         else if(ch=='g') tS[i] = 2;
 60         else if(ch=='m') tS[i] = 3;
 61         else if(ch=='b') tS[i] = 4;
 62         else tS[i] = 5;
 63     }
 64 }
 65 
 66 int bfs(){
 67     map<LL, bool> vis[31][31][7];
 68     queue<node> q;
 69     vis[Sx][Sy][0][43210] = true;
 70    q.push(node(Sx,Sy,43210,0,0));
 71 
 72    while(q.size()){
 73         node p = q.front();q.pop();
 74         if(p.nowID==6) return p.step;
 75         getNum(p.state);
 76         int mubic = tS[p.nowID];
 77         for(int i=0;i<4;i++){
 78             int x = p.x + xx[i] , y = p.y + yy[i];
 79             if(x<0||x>=n||y<0||y>=m||ditu[x][y]==-2) continue;
 80             int state = change(p.state,i);
 81             int top = state % 10;
 82             int nowID = p.nowID;
 83             if(ditu[x][y]!=-1){
 84                 if(ditu[x][y]!=mubic||top != mubic) continue;
 85                 else nowID = p.nowID + 1;
 86             }
 87             if(vis[x][y][nowID][state]) continue;
 88             vis[x][y][nowID][state] = true;
 89             q.push(node(x,y,state,nowID,p.step+1));
 90         }
 91    }
 92 
 93    return -1;
 94 }
 95 
 96 int main()
 97 {
 98     while(cin>>m>>n&&n&&m){
 99             init();
100             int ans = bfs();
101             if(ans==-1) puts("unreachable");
102             else cout<<ans<<endl;
103     }
104     return 0;
105 }

View Code

优化：这里看了其他人代码，其实还可以优化，颜色就只有6种，6个不同位置，所以6进制就行。并且因为箱子颜色是固定的，所以只要记录3个面就行了。颜色划分0~5，所以，状态最大只需要5*36+4*6+3=207 所以vis只需要开到 vis[31][31][208][7]

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 #include <set>
  9 
 10 using namespace std;
 11 
 12 #define LL long long
 13 
 14 const int INF = 0x3f3f3f3f;
 15 
 16 // r-0 c-5 g-2 m-3 b-1 y-4
 17 int n,m,Sx,Sy;
 18 int tS[6];
 19 int ditu[31][31];//w- -1 k- -2
 20 bool vis[31][31][208][7];
 21 int xx[]={0,0,-1,1};
 22 int yy[]={1,-1,0,0};
 23 
 24 struct node{
 25     int x,y,state,nowID,step;
 26     node(int a,int b,int c,int d,int e):x(a),y(b),state(c),nowID(d),step(e) {};
 27     void show(){
 28         cout<<x<<' '<<y<<' '<<state<<' '<<nowID<<' '<<step<<endl;
 29     }
 30 };
 31 
 32 int num[6];
 33 void getNum(int x){
 34     num[0] = x%6; x/=6;
 35     num[1] = x%6; x/=6;
 36     num[2] = x;
 37     num[3] = 5 - num[2];
 38     num[4] = 5 - num[1];
 39     num[5] = 5 - num[0];
 40 }
 41 int change(int i){
 42     if(i==0) return  num[2]*36 + num[0]*6 + num[4];
 43     if(i==1) return  num[2]*36 + num[5]*6 + num[1];
 44     if(i==2) return  num[0]*36 + num[1]*6+ num[3];
 45     return  num[5]*36 + num[1]*6 + num[2];
 46 }
 47 
 48 void init(){
 49     memset(ditu,-1,sizeof ditu);
 50     for(int i=0;i<n;i++)
 51         for(int j=0;j<m;j++){
 52             char ch=getchar();while(ch=='\n'||ch==' ') ch=getchar();
 53             if(ch=='#') Sx = i,Sy = j;
 54             else if(ch=='k') ditu[i][j] = -2;else if(ch=='r') ditu[i][j] = 0;else if(ch=='c') ditu[i][j] = 5;
 55             else if(ch=='g') ditu[i][j] = 2;else if(ch=='m') ditu[i][j] = 3;else if(ch=='b') ditu[i][j] = 1;else if(ch=='y') ditu[i][j] = 4;
 56     }
 57     for(int i=0;i<6;i++){
 58         char ch=getchar();while(ch=='\n'||ch==' ') ch=getchar();
 59         if(ch=='r') tS[i] = 0;
 60         else if(ch=='c') tS[i] = 5;
 61         else if(ch=='g') tS[i] = 2;
 62         else if(ch=='m') tS[i] = 3;
 63         else if(ch=='b') tS[i] = 1;
 64         else tS[i] = 4;
 65     }
 66 }
 67 
 68 int bfs(){
 69     queue<node> q;
 70     memset(vis,false,sizeof vis);
 71     vis[Sx][Sy][78][0] = true;
 72    q.push(node(Sx,Sy,78,0,0));
 73 
 74    while(q.size()){
 75         node p = q.front();q.pop();
 76         if(p.nowID==6) return p.step;
 77         getNum(p.state);
 78         int mubic = tS[p.nowID];
 79         for(int i=0;i<4;i++){
 80             int x = p.x + xx[i] , y = p.y + yy[i];
 81             if(x<0||x>=n||y<0||y>=m||ditu[x][y]==-2) continue;
 82             int state = change(i);
 83             int top = state % 6;
 84             int nowID = p.nowID;
 85             if(ditu[x][y]!=-1){
 86                 if(ditu[x][y]!=mubic||top != mubic) continue;
 87                 else nowID = p.nowID + 1;
 88             }
 89             if(vis[x][y][state][nowID]) continue;
 90             vis[x][y][state][nowID] = true;
 91             q.push(node(x,y,state,nowID,p.step+1));
 92         }
 93    }
 94 
 95    return -1;
 96 }
 97 
 98 int main()
 99 {
100     while(cin>>m>>n&&n&&m){
101             init();
102             int ans = bfs();
103             if(ans==-1) puts("unreachable");
104             else cout<<ans<<endl;
105     }
106     return 0;
107 }

View Code

GemAnd PrinceHDU - 4090

题意：消消乐，消除后宝石自动向左向下靠，3个以上才能消，8各方向算。（前面有三道题一样是消消乐，代码直接拿来用就行了）

算法：dfs+剪枝

思路：简单dfs，然后预估函数潜在最大价值就是，直接找出每种宝石的数量总和的平方和。

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 
 9 using namespace std;
10 
11 const int INF = 0x3f3f3f3f;
12 
13 int n,m,k,ans;
14 int xx[]={0,0,-1,1,-1,-1,1,1};
15 int yy[]={1,-1,0,0,1,-1,1,-1};
16 int ditu[8][8];
17 int cnt;
18 
19 void init(){
20     for(int i=0;i<n;i++)
21         for(int j=0;j<m;j++) cin>>ditu[i][j];
22     ans = 0;
23 }
24 
25 int eval(){
26     int res[7] = {0};
27     int tmp = 0;
28     for(int i=0;i<n;i++)
29         for(int j=0;j<m;j++)
30             if(ditu[i][j]) res[ditu[i][j]]++;
31     for(int i=1;i<=k;i++) tmp += res[i]*res[i];
32     return tmp;
33 }
34 
35 //清零之后的向左向下靠齐
36 void remake(){
37     int tmp[8][8];
38     memset(tmp,0,sizeof tmp);
39     int tmpX,tmpY=0;
40     for(int j=0;j<m;j++){
41         bool flag = false;
42         tmpX = n-1;
43         for(int i=n-1;i>=0;i--){
44             if(ditu[i][j]==0) continue;
45             flag=true;
46             tmp[tmpX--][tmpY] = ditu[i][j];
47         }
48         if(flag) tmpY++;
49     }
50     memcpy(ditu,tmp,sizeof ditu);
51 }
52 
53 //坐标(a,b)向外扩展清零
54 void  clean(int a,int b,int c,bool vis[8][8]){
55     for(int i=0;i<8;i++){
56         int x = a + xx[i] ,  y = b + yy[i];
57         if(x<0||x>=n||y<0||y>=m||ditu[x][y]!=c||vis[x][y]) continue;
58         vis[x][y] = true,ditu[x][y]=0,cnt++;
59         clean(x,y,c,vis);
60     }
61 }
62 
63 void show(){
64     puts("------------------------------");
65     for(int i=0;i<n;i++){for(int j=0;j<m;j++) cout<<ditu[i][j]<<" ";cout<<endl;}
66     puts("------------------------------");
67 }
68 
69 void dfs(int now){
70     if(ans<now) ans = now;
71     if(now+eval()<=ans) return ;
72     int res[8][8];
73     memcpy(res,ditu,sizeof res);
74     bool vis[8][8];
75     memset(vis,false,sizeof vis);
76     //show();cout<<now<<" "<<ans<<endl;
77     for(int i=0;i<n;i++)
78         for(int j=0;j<m;j++) if(ditu[i][j]&&!vis[i][j]){
79             vis[i][j]=true;cnt = 1;
80             clean(i,j,ditu[i][j],vis);ditu[i][j]=0;
81             if(cnt>=3){
82                 remake();
83                 dfs(now+cnt*cnt);
84             }
85             memcpy(ditu,res,sizeof ditu);
86         }
87 }
88 
89 int main()
90 {
91     while(cin>>n>>m>>k){
92         init();
93         dfs(0);
94         cout<<ans<<endl;
95     }
96     return 0;
97 }

View Code

SolitaireHDU - 1401

题意：一个8*8的地图，4个相同的棋子，然后给出两个布局，问从布局1到布局2,8步内是否能完成？棋子只能上下左右走一格，或者可以隔着一个棋子跳一格。

算法：状压+双向bfs

思路：状压：因为8*8地图，坐标可以变成（0~7），所以可以3位二进制表示，4个棋子就只需要24位，用一个int。然后因为相同棋子，所以状压之前需要排序。

　　　一开始用了dfs，TLE了，后面用双向bfs，一层层进行，只进行4层。

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 
  9 using namespace std;
 10 
 11 const int INF = 0x3f3f3f3f;
 12 
 13 int xx[]={1,0,-1,0};
 14 int yy[]={0,1,0,-1};
 15 
 16 struct po{
 17     int x,y;
 18     bool operator < (const po &a){
 19         if(x==a.x) return y<a.y;
 20         return x<a.x;
 21     }
 22 };
 23 
 24 struct node{
 25     po pp[4];
 26     int step;
 27     int makeHash(){
 28         sort(pp,pp+4);
 29         int tmp = 0;
 30         tmp += pp[0].x;tmp<<=3;tmp += pp[0].y;tmp<<=3;tmp += pp[1].x;tmp<<=3;tmp += pp[1].y;tmp<<=3;
 31         tmp += pp[2].x;tmp<<=3;tmp += pp[2].y;tmp<<=3;tmp += pp[3].x;tmp<<=3;tmp += pp[3].y;
 32         return tmp;
 33     }
 34 }s,t;
 35 
 36 int one;
 37 void init(){
 38     s.pp[0].x = one-1;
 39     cin>>one;s.pp[0].y = one-1;
 40     for(int i=1;i<4;i++){
 41         int a,b;cin>>a>>b;
 42         s.pp[i].x = a-1,s.pp[i].y = b-1;
 43     }
 44     for(int i=0;i<4;i++){
 45         int a,b;cin>>a>>b;
 46         t.pp[i].x = a-1,t.pp[i].y = b-1;
 47     }
 48 }
 49 
 50 bool check(int x,int y,node a){
 51     for(int i=0;i<4;i++){
 52         if(a.pp[i].x==x&&a.pp[i].y==y) return true;
 53     }
 54     return false;
 55 }
 56 
 57 bool bfs(){
 58     map<int,bool> mp1;
 59     map<int,bool> mp2;
 60     int a = s.makeHash() , b = t.makeHash();
 61     if(a==b) return true;
 62     mp1[a] = true;
 63     mp2[b] = true;
 64     s.step = 0;t.step=0;
 65     queue<node> q1;q1.push(s);
 66     queue<node> q2;q2.push(t);
 67     int step = 0;
 68     while(q1.size()&&q2.size()&&step<4){
 69 
 70         while(q1.size()){
 71             node p1 = q1.front();
 72             if(mp2[p1.makeHash()]) return true;
 73             if(p1.step>step) break;
 74             else q1.pop();
 75 
 76             for(int cN=0;cN<4;cN++){
 77                 for(int i=0;i<4;i++){
 78                     int x = p1.pp[cN].x + xx[i] , y =  p1.pp[cN].y + yy[i];
 79                     if(x<0||x>=8||y<0||y>=8) continue;
 80                     if(check(x,y,p1)){
 81                         x+=xx[i], y+=yy[i];
 82                         if(x<0||x>=8||y<0||y>=8) continue;
 83                         if(check(x,y,p1)) continue;
 84                         node u = p1;
 85                         u.pp[cN].x = x , u.pp[cN].y = y;
 86                         int tmp = u.makeHash();
 87                         if(mp2[tmp]) return true;
 88                         if(mp1[tmp]) continue;
 89                         mp1[tmp] = true;
 90                         u.step++;q1.push(u);
 91                     }else{
 92                         node u = p1;
 93                         u.pp[cN].x = x , u.pp[cN].y = y;
 94                         int tmp = u.makeHash();
 95                         if(mp2[tmp]) return true;
 96                         if(mp1[tmp]) continue;
 97                         mp1[tmp] = true;
 98                         u.step++;q1.push(u);
 99                     }
100                 }
101             }
102         }
103 //----------------------------------------------------------------------
104         while(q2.size()){
105             node p2 = q2.front();
106             if(mp1[p2.makeHash()]) return true;
107             if(p2.step>step) break;
108             else q2.pop();
109 
110             for(int cN=0;cN<4;cN++){
111                 for(int i=0;i<4;i++){
112                     int x = p2.pp[cN].x + xx[i] , y =  p2.pp[cN].y + yy[i];
113                     if(x<0||x>=8||y<0||y>=8) continue;
114                     if(check(x,y,p2)){
115                         x+=xx[i], y+=yy[i];
116                         if(x<0||x>=8||y<0||y>=8) continue;
117                         if(check(x,y,p2)) continue;
118                         node u = p2;
119                         u.pp[cN].x = x , u.pp[cN].y = y;
120                         int tmp = u.makeHash();
121                         if(mp1[tmp]) return true;
122                         if(mp2[tmp]) continue;
123                         mp2[tmp] = true;
124                         u.step++;q2.push(u);
125                     }else{
126                         node u = p2;
127                         u.pp[cN].x = x , u.pp[cN].y = y;
128                         int tmp = u.makeHash();
129                         if(mp1[tmp]) return true;
130                         if(mp2[tmp]) continue;
131                         mp2[tmp] = true;
132                         u.step++;q2.push(u);
133                     }
134                 }
135             }
136         }
137         step++;
138     }
139     return false;
140 }
141 
142 int main()
143 {
144     while(cin>>one){
145         init();
146         if(bfs()) puts("YES");
147         else puts("NO");
148     }
149     return 0;
150 }

View Code

Flood-it!HDU - 4127

题意：8*8的地图，然后有6中颜色，对左上角进行着色，每一次着色都会把相同颜色划分到一起，下次会跟着左上角一起变色，问将所有地图变成一种颜色的最小步数。

算法：IDAstar

思路：因为求最小，所以每次状态都预估一个到达目标的最小步数，这题的最小步数就是剩余多少颜色与左上角不同。

易错点：每次操作都需要找相邻的点的颜色进行对左上角着色，这里使用vis数组，1表示已经着色过，与左上角颜色一致；2表示相邻的点；然后每次操作，只需要列举颜色就行了。

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 
 9 using namespace std;
10 
11 const int INF = 0x3f3f3f3f;
12 
13 int ditu[8][8];
14 int vis[8][8];
15 int n,nextd;
16 int xx[]={1,-1,0,0};
17 int yy[]={0,0,1,-1};
18 
19 int dis_h(){
20     int res = 0;
21     int visC[6]={0};
22     for(int i=0;i<n;i++)
23         for(int j=0;j<n;j++) if(vis[i][j]!=1&&!visC[ditu[i][j]]){
24             visC[ditu[i][j]] = 1;
25             res++;
26         }
27     return res;
28 }
29 
30 void dfs(int a,int b,int c){
31     vis[a][b] = 1;
32     for(int i=0;i<4;i++){
33         int x = a + xx[i] , y = b + yy[i];
34         if(x<0||x>=n||y<0||y>=n||vis[x][y]) continue;
35         if(ditu[x][y]==c) dfs(x,y,c);
36         else vis[x][y]=2;
37     }
38 }
39 
40 bool color(int c){
41     bool res = false;
42     for(int i=0;i<n;i++)
43         for(int j=0;j<n;j++) if(ditu[i][j]==c&&vis[i][j]==2){
44             res=true;
45             dfs(i,j,c);
46     }
47     return res;
48 }
49 
50 bool IDAstar(int depth,int limit){
51     int h = dis_h();
52     if(depth+h>limit){
53         nextd = min(nextd, depth+h);
54         return false;
55     }
56     if(h==0){
57         cout<<depth<<endl;
58         return true;
59     }
60     int visT[8][8];
61     memcpy(visT,vis,sizeof visT);
62     for(int i=0;i<6;i++){
63         if(!color(i)) continue;
64         if(IDAstar(depth+1,limit)) return true;
65         memcpy(vis,visT,sizeof vis);
66     }
67     return false;
68 }
69 
70 void init(){
71     for(int i=0;i<n;i++)
72         for(int j=0;j<n;j++) cin>>ditu[i][j];
73     memset(vis,0,sizeof vis);
74     dfs(0,0,ditu[0][0]);
75 }
76 
77 int main()
78 {
79     while(cin>>n&&n){
80         init();
81         for(int limit=dis_h();;limit=nextd){
82             nextd = INF;
83             if(IDAstar(0,limit)) break;
84         }
85     }
86     return 0;
87 }

View Code

IslandsHDU - 2808

题意：就是100*100的地图，上面有海和岛，岛是8各方向判断是否连接的，然后如果一座岛里面没有其他岛的话，他的岛等级就是0，如果存在其他岛的话，他的等级就是他的子岛最大等级+1.

算法：dfs

思路：这题和前面那道埃及文字题目差不多，Ancient Messages HDU - 3839。就是从边缘开始判断，海的话就进行dfs判断，把所有外海标记了，然后与外海邻接的岛就记录；然后在从这些岛开始dfs判断，一座岛一座岛标记，然后每次都把与这些岛邻接的内海进行记录，再对这些内海进行标记，反正就是互相套娃。当一座岛里面没有海或者内海里面没有外岛，他的等级就是0了。

易错点：注意细节，耐心耐心耐心

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 
  9 using namespace std;
 10 
 11 const int INF = 0x3f3f3f3f;
 12 
 13 char ditu[100][100];
 14 bool vis[100][100];
 15 bool visB[100][100];
 16 bool visW[100][100];
 17 int n,m;
 18 int xx[]={1,-1,0,0,-1,-1,1,1};
 19 int yy[]={0,0,1,-1,-1,1,1,-1};
 20 int ans[100],ansN;
 21 
 22 void show(){
 23     for(int i=0;i<n;i++){
 24         for(int j=0;j<m;j++) cout<<ditu[i][j];cout<<endl;
 25     }cout<<endl;
 26 }
 27 
 28 void init(){
 29     for(int i=0;i<n;i++) cin>>ditu[i];
 30     memset(vis,false,sizeof vis);
 31     memset(visB,false,sizeof visB);
 32     memset(visW,false,sizeof visW);
 33     memset(ans,0,sizeof ans);
 34     ansN = -1;
 35 }
 36 
 37 struct node{
 38     int x,y;
 39     node(int a,int b):x(a),y(b) {};
 40 };
 41 
 42 void show2(vector<node> a){
 43     cout<<"vector: ";
 44     for(int i=0;i<a.size();i++){
 45         cout<<a[i].x<<" "<<a[i].y<<" | ";
 46     }cout<<endl;
 47 }
 48 
 49 void show3(){
 50     for(int i=0;i<n;i++){
 51         for(int j=0;j<m;j++) cout<<vis[i][j]<<" ";cout<<endl;
 52     }cout<<endl;
 53 }
 54 
 55 void  cleanW(int a,int b,vector<node> &v){
 56     vis[a][b]=true;
 57     for(int i=0;i<4;i++){
 58         int x = a + xx[i] , y = b+ yy[i];
 59         if(x<0||x>=n||y<0||y>=m||vis[x][y]) continue;
 60         if(ditu[x][y]=='.') cleanW(x,y,v);
 61         else if(!visB[x][y]) visB[x][y] = true,v.push_back(node(x,y));
 62     }
 63 }
 64 
 65 void  cleanB(int a,int b,vector<node> &v,int &c){
 66     vis[a][b]=true;c++;
 67     for(int i=0;i<8;i++){
 68         int x = a + xx[i] , y = b+ yy[i];
 69         if(x<0||x>=n||y<0||y>=m||vis[x][y]) continue;
 70         if(ditu[x][y]=='x') cleanB(x,y,v,c);
 71         else if(!visW[x][y]) visW[x][y] = true,v.push_back(node(x,y));
 72     }
 73 }
 74 
 75 int dfs(int x,int y) {
 76     vector<node> v,v2;
 77     int res = 0;
 78     int level = 0;
 79     cleanB(x,y,v,res);
 80     if(v.size()==0) {ans[0]+=res;return 0;}
 81     //show2(v);show3();
 82     for(int i=0;i<v.size();i++){
 83         int a = v[i].x , b = v[i].y;
 84         if(vis[a][b]) continue;
 85         cleanW(a,b,v2);
 86     }
 87    // show2(v2);show3();
 88     if(v2.size()==0) {ans[0]+=res;return 0;}
 89     for(int i=0;i<v2.size();i++){
 90         int a = v2[i].x , b = v2[i].y;
 91         if(vis[a][b]) continue;
 92         level  = max(level,dfs(a,b)+1);
 93     }
 94     ans[level]+=res;
 95     return level;
 96 };
 97 
 98 void solve(){
 99     vector<node> v;
100     for(int i=0;i<n;i++){
101         if(!vis[i][0]){
102             if(ditu[i][0]=='.') cleanW(i,0,v);
103             else if(!visB[i][0]) visB[i][0] = true,v.push_back(node(i,0));
104         }
105         if(!vis[i][m-1]){
106             if(ditu[i][m-1]=='.') cleanW(i,m-1,v);
107             else if(!visB[i][m-1]) visB[i][m-1] = true,v.push_back(node(i,m-1));
108         }
109     }
110     for(int j=1;j<m-1;j++){
111         if(!vis[0][j]){
112             if(ditu[0][j]=='.') cleanW(0,j,v);
113             else if(!visB[0][j]) visB[0][j] = true,v.push_back(node(0,j));
114         }
115         if(!vis[n-1][j]){
116             if(ditu[n-1][j]=='.') cleanW(n-1,j,v);
117             else if(!visB[n-1][j]) visB[n-1][j] = true,v.push_back(node(n-1,j));
118         }
119     }
120 //------------------------------------------------------------------------------------
121     //show2(v);show3();
122     for(int i=0;i<v.size();i++){
123         int a = v[i].x , b = v[i].y;
124         if(vis[a][b]) continue;
125         ansN  = max(ansN,dfs(a,b));
126     }
127 }
128 
129 int main()
130 {
131     while(cin>>n>>m){
132         init();//show();
133         solve();
134         //cout<<ansN<<endl;
135         if(ansN==-1) {cout<<endl;continue;}
136         for(int i=0;i<ansN;i++) cout<<ans[i]<<" ";cout<<ans[ansN]<<endl;
137     }
138     return 0;
139 }

View Code

魔板HDU - 1430

题意：给两个字符串，有3种字符串操作方式，问从字符串1到字符串2最小步数

算法：bfs预处理

思路：和前面 A - Eight HDU - 1043 题目思路一样，不赘述了。

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 
 9 using namespace std;
10 
11 const int INF = 0x3f3f3f3f;
12 
13 char s[9],t[9];
14 map<string,string> mp;
15 
16 struct node{
17     char  s[9];
18     node(char a[9]) {
19         for(int i=0;i<8;i++) s[i] = a[i];
20         s[8]='\0';
21     }
22 };
23 
24 void changeA(char (&b)[9],char a[9]){
25     b[0] = a[7];
26     b[1] = a[6];
27     b[2] = a[5];
28     b[3] = a[4];
29     b[4] = a[3];
30     b[5] = a[2];
31     b[6] = a[1];
32     b[7] = a[0];
33     b[8] = '\0';
34 }
35 //41236785
36 void changeB(char (&b)[9],char a[9]){
37     b[0] = a[3];
38     b[1] = a[0];
39     b[2] = a[1];
40     b[3] = a[2];
41     b[4] = a[5];
42     b[5] = a[6];
43     b[6] = a[7];
44     b[7] = a[4];
45     b[8] = '\0';
46 }
47 //17245368
48 void changeC(char (&b)[9],char a[9]){
49     b[0] = a[0];
50     b[1] = a[6];
51     b[2] = a[1];
52     b[3] = a[3];
53     b[4] = a[4];
54     b[5] = a[2];
55     b[6] = a[5];
56     b[7] = a[7];
57     b[8] = '\0';
58 }
59 
60 void bfs(){
61     char s[9];for(int i=0;i<8;i++) s[i] = '0' + i + 1;s[8] = '\0';
62     mp[s] = "";
63     queue<node> q;
64     q.push(node(s));
65 
66     while(q.size()){
67         node p = q.front();q.pop();
68         //A---------------------------------------------
69         char ch[9];
70         changeA(ch,p.s);
71         if(!(mp.find(ch)!=mp.end())){mp[ch]=mp[p.s]+"A";q.push(node(ch));}
72         //B----------------------------------
73         changeB(ch,p.s);
74         if(!(mp.find(ch)!=mp.end())){mp[ch]=mp[p.s]+"B";q.push(node(ch));}
75         //C------------------------------------
76          changeC(ch,p.s);
77         if(!(mp.find(ch)!=mp.end())){mp[ch]=mp[p.s]+"C";q.push(node(ch));}
78     }
79 }
80 
81 int main()
82 {
83     bfs();
84     while(cin>>s>>t){
85         s[8]='\0';t[8]='\0';
86         int c[9];
87         for(int i=0;i<8;i++) c[s[i]-'0'] = '0'+i+1;
88         for(int i=0;i<8;i++) t[i] = c[t[i]-'0'];
89         //cout<<t<<endl;
90         cout<<mp[t]<<endl;
91     }
92     return 0;
93 }

View Code

The Rotation Gam HDU - 1667

题意：一个玩具，可以8个方向转动，有3种方块，问将中间的数字都变成一样的最小步数

算法：IDAstar

思路：之前状压魔怔了，其实这里可以不需要判重，因为每一次操作对整体影响都很大，而且组成部分也是分成3种方块，如果操作许多步数才能变回同一状态，这里求得最小步数，同时用的dfs，所以不需要判重，但是判重会快一点，或者加点剪枝；启发函数，就是求中间8个方块的最大颜色总和x，然后8-x，至少需要8-x步数；这里剪枝就是不走上一步相反的操作。因为正反会抵消。

易错点：这里一定要按照字母顺序进行向下搜索，因为答案需要最小字母顺序

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 
 9 using namespace std;
10 
11 const int INF = 0x3f3f3f3f;
12 
13 int nextd,one;
14 int ans,tmpC;
15 string ansStr,tmpStr;
16 int num[24];
17 int cg[8][7]={{ 0, 2, 6,11,15,20,22},{ 1, 3, 8,12,17,21,23},{10, 9, 8, 7, 6, 5, 4},{19,18,17,16,15,14,13},
18                                 {23,21,17,12, 8, 3, 1},{22,20,15,11, 6, 2, 0},{13,14,15,16,17,18,19},{ 4, 5, 6, 7, 8, 9,10}};
19 int ck[8] ={6,7,8,11,12,15,16,17};
20 
21 int dis_h(){
22     int res[4]= {0};
23     for(int i=0;i<8;i++) res[num[ck[i]]]++;
24     int maxNum = res[1];tmpC  = 1;
25     if(maxNum<res[2]) maxNum = res[2] , tmpC = 2;
26     if(maxNum<res[3]) maxNum = res[3] , tmpC = 3;
27     return maxNum;
28 }
29 
30 void init(){
31     num[0]=one;
32     for(int i=1;i<24;i++) cin>>num[i];
33     ansStr="";
34 }
35 
36 bool IDAstar(int step,int limit,int id){
37     int h = 8 - dis_h();
38     if(h+step>limit){
39         nextd = min(nextd,h+step);
40         return false;
41     }
42     if(h==0){
43         if(ansStr.length()<step||(ansStr.length()==step&&ansStr>tmpStr)) ans = tmpC , ansStr = tmpStr;
44         return true;
45     }
46     for(int i=0;i<8;i++){
47         if((id==0&&i==5)||(id==5&&i==0)||(id==1&&i==4)||(id==4&&i==1)||(id==2&&i==7)||(id==7&&i==2)||(id==3&&i==6)||(id==6&&i==3)) continue;
48         string tmpS = tmpStr;
49         int c = num[cg[i][0]];
50         for(int j=0;j<6;j++) num[cg[i][j]] = num[cg[i][j+1]];
51         num[cg[i][6]] = c;
52         tmpStr+='A'+i;
53         if(IDAstar(step+1,limit,i)) return true;
54         tmpStr = tmpS;
55         c = num[cg[i][6]];
56         for(int j=6;j>0;j--) num[cg[i][j]] = num[cg[i][j-1]];
57         num[cg[i][0]] = c;
58     }
59     return false;
60 }
61 
62 void solve(){
63     int limit = 8 - dis_h();
64     if(limit==0) {puts("No moves needed");cout<<tmpC<<endl;return ;}
65     //-------------------------------------------------------------
66     for(bool flag=true;flag;limit = nextd){
67         nextd = INF;
68         tmpStr = "";
69         if(IDAstar(0,limit,-1)) break;
70     }
71     cout<<ansStr<<endl;
72     cout<<ans<<endl;
73 }
74 
75 int main()
76 {
77     while(cin>>one&&one){
78         init();
79         solve();
80     }
81     return 0;
82 }

View Code

思路2：这种思路用了状压，同时可以判重。因为只有3种颜色，只记录一种颜色的分布情况，用24位二进制记录，启发函数和思路1一样，中间不是该颜色的总和；然后进行三种颜色的IDAstar搜索；

易错点：这题判重不是重点，重点是字母顺序操作+启发函数的编写

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 
  9 using namespace std;
 10 
 11 const int INF = 0x3f3f3f3f;
 12 
 13 int nextd,one,two,three;
 14 int ans,ansLen;
 15 string ansStr,tmpStr;
 16 int num[24];
 17 bool vis[3][1<<24];
 18 
 19 int cg[8][7]={{ 0, 2, 6,11,15,20,22},{ 1, 3, 8,12,17,21,23},{10, 9, 8, 7, 6, 5, 4},{19,18,17,16,15,14,13},
 20                                 {23,21,17,12, 8, 3, 1},{22,20,15,11, 6, 2, 0},{13,14,15,16,17,18,19},{ 4, 5, 6, 7, 8, 9,10}};
 21 int ck[8] ={6,7,8,11,12,15,16,17};
 22 
 23 int dis_h(int x){
 24     int res = 0;
 25     for(int i=0;i<8;i++) if((x&1<<ck[i])==0) res++;
 26     return res;
 27 }
 28 
 29 void init(){
 30     num[0]=one;
 31     for(int i=1;i<24;i++) cin>>num[i];
 32     one = 0 , two = 0 , three = 0;
 33     ansLen = 0;ansStr="";
 34     memset(vis,false,sizeof vis);
 35     for(int i=0;i<24;i++){
 36         if(num[i]==1) one |= 1<<i;
 37         else if(num[i]==2) two |= 1<<i;
 38         else three |= 1<<i;
 39     }
 40 }
 41 
 42 bool IDAstar(int n,int c,int step,int limit){
 43     int h = dis_h(n);
 44     if(h+step>limit){
 45         nextd = min(nextd,h+step);
 46         return false;
 47     }
 48     if(h==0){
 49         if(ansLen<step||(ansLen==step&&ansStr>tmpStr)) {
 50                 ansLen = step;
 51                 ans = c , ansStr = tmpStr;
 52                 //cout<<ansLen<<" "<<ans<<" "<<ansStr<<endl;
 53         }
 54         return true;
 55     }
 56     for(int i=0;i<8;i++){
 57         int tmp = n;
 58         bool flag = false;
 59         string tmpS = tmpStr;
 60         if(tmp&1<<cg[i][0]) flag = true;
 61         for(int j=0;j<6;j++){
 62             if(tmp&1<<cg[i][j]) tmp^=1<<cg[i][j];
 63             if(tmp&1<<cg[i][j+1]) tmp|=1<<cg[i][j];
 64         }
 65         if(tmp&1<<cg[i][6]) tmp^=1<<cg[i][6];
 66         if(flag) tmp|=1<<cg[i][6];
 67         if(vis[c-1][tmp]) continue;
 68         tmpStr+='A'+i;
 69         vis[c-1][tmp]=true;
 70         if(IDAstar(tmp,c,step+1,limit)) return true;
 71         vis[c-1][tmp]=false;
 72         tmpStr = tmpS;
 73     }
 74     return false;
 75 }
 76 
 77 void solve(){
 78     int a = dis_h(one) , b = dis_h(two) , c=dis_h(three);
 79     if(a==0) {puts("No moves needed");puts("1");return ;}
 80     if(b==0) {puts("No moves needed");puts("2");return ;}
 81     if(c==0) {puts("No moves needed");puts("3");return ;}
 82     int limit = min(a,min(b,c));
 83     vis[0][one] = true , vis[1][two] = true , vis[2][three] = true;
 84     //-------------------------------------------------------------
 85     for(bool flag=true;flag;limit = nextd){
 86         nextd = INF;
 87         tmpStr = "";
 88         if(IDAstar(one,1,0,limit)) flag=false;
 89         tmpStr = "";
 90         if(IDAstar(two,2,0,limit)) flag=false;
 91         tmpStr = "";
 92         if(IDAstar(three,3,0,limit)) flag=false;
 93     }
 94     cout<<ansStr<<endl;
 95     cout<<ans<<endl;
 96 }
 97 
 98 int main()
 99 {
100     while(cin>>one&&one){
101         init();
102         solve();
103     }
104     return 0;
105 }

View Code

无题IHDU - 2234

题意：给出一个4*4地图，元素：1、2、3、4分别有4个，4种操作：行的左右转动、列的上下转动；问给出一个随机状态，问需要多少步（5步内）可以使这个地图，要不行全相同，或者列相同。

算法：IDAstar

思路：启发函数，首先是找行，因为每一行之间是相互影响的，合作关系找最大，所以一行的至少操作步数：找出一行里面最大相同元素总和x，然后4-x，然后再从这至少操作数里面找最大，得a；列同理可得b。因为行和列只要其中一个达到条件都行，竞争关系找最小，所以是min(a,b);我这里和上一题一样，加了个不走上一步相反操作的剪枝。

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 
 9 using namespace std;
10 
11 const int INF = 0x3f3f3f3f;
12 
13 int ditu[4][4],nextd;
14 void turn(int x){
15     int t = ditu[x][0];
16     for(int i=0;i<3;i++) ditu[x][i] = ditu[x][i+1];
17     ditu[x][3] = t;
18 }
19 void turn2(int x){
20     int t = ditu[x][3];
21     for(int i=3;i>0;i--) ditu[x][i] = ditu[x][i-1];
22     ditu[x][0] = t;
23 }
24 void turn3(int x){
25     int t = ditu[0][x];
26     for(int i=0;i<3;i++) ditu[i][x] = ditu[i+1][x];
27     ditu[3][x] = t;
28 }
29 void turn4(int x){
30     int t = ditu[3][x];
31     for(int i=3;i>0;i--) ditu[i][x] = ditu[i-1][x];
32     ditu[0][x] = t;
33 }
34 int dis_h(){
35     int a = 0;
36     for(int i=0;i<4;i++){
37         int ans=0,num[4]={0};
38         for(int j=0;j<4;j++) num[ditu[i][j]-1]++;
39         for(int j=0;j<4;j++) ans = max(ans,num[j]);
40         a = max(a,4-ans);
41     }
42     int b=0;
43     for(int i=0;i<4;i++){
44         int ans=0,num[4]={0};
45         for(int j=0;j<4;j++) num[ditu[j][i]-1]++;
46         for(int j=0;j<4;j++) ans = max(ans,num[j]);
47         b = max(b,4-ans);
48     }
49     return min(a,b);
50 }
51 bool IDAstar(int step,int limit,int id,int cz,int cd){
52     int h = dis_h();
53     if(step+h>limit) {nextd=min(nextd,step+h);return false;}
54     if(h==0) {cout<<step<<endl;return true;}
55     for(int x=0;x<4;x++){
56         if(!(id==x&&cz==0&&cd==0)){
57             turn(x);
58             if(IDAstar(step+1,limit,x,1,0)) return true;
59             turn2(x);
60         }
61         if(!(id==x&&cz==1&&cd==0)){
62             turn2(x);
63             if(IDAstar(step+1,limit,x,0,0)) return true;
64             turn(x);
65         }
66         if(!(id==x&&cz==0&&cd==1)){
67             turn3(x);
68             if(IDAstar(step+1,limit,x,1,1)) return true;
69             turn4(x);
70         }
71         if(!(id==x&&cz==1&&cd==1)){
72             turn4(x);
73             if(IDAstar(step+1,limit,x,0,1)) return true;
74             turn3(x);
75         }
76     }
77     return false;
78 }
79 
80 int main()
81 {
82     int _;cin>>_;
83     while(_--){
84         for(int i=0;i<4;i++)
85             for(int j=0;j<4;j++) cin>>ditu[i][j];
86         int limit=dis_h();
87         if(limit==0) {puts("0");continue;}
88         for(;limit<6;limit=nextd){
89             nextd = INF;
90             if(IDAstar(0,limit,-1,-1,-1)) break;
91         }
92         if(limit>5) puts("-1");
93     }
94     return 0;
95 }

View Code

Escape from Tetris HDU - 1813

题意：给你一副0、1地图，1表示墙壁，出口是边界，走到边界的0也算出去了，你可以走东南西北4个方向，问是否存在一个最小步数的操作，使你不管在地图上的任意一点都能靠这个操作走出去？如果你的这个操作撞墙的话，就原地等待下一个操作。

算法：IDAstar

思路：预处理，从边界0进行入队，求出所有点到边界0的最小距离。然后IDAstar 从所有非边界0开始，一步步向下搜索，如果走到边界就消除，撞墙就原地等待，每个步骤都维护一个当前还有多少个没有走出去，启发函数就是求这些还没走出去的距离出口最远的距离。

易错点：这里是每个测试数据答案之间有空行

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 
  9 using namespace std;
 10 
 11 const int INF = 0x3f3f3f3f;
 12 
 13 int n,dis[9][9],nextd;
 14 int ans[82];
 15 bool vis[9][9];
 16 char ditu[9][9];
 17 int xx[4]={0,-1,1,0};
 18 int yy[4]={1,0,0,-1};
 19 
 20 void show(){
 21     for(int i=0;i<n;i++){
 22         for(int j=0;j<n;j++) cout<<vis[i][j]<<" ";cout<<endl;
 23     }cout<<endl;
 24 }
 25 void init(){
 26     for(int i=0;i<n;i++) cin>>ditu[i];
 27     memset(dis,INF,sizeof dis);
 28     memset(vis,false,sizeof vis);
 29     queue<pair<int,int>> q;
 30     for(int i=0;i<n;i++){
 31         if(ditu[i][0]=='0') dis[i][0]=0,q.push(make_pair(i,0));
 32         if(ditu[i][n-1]=='0') dis[i][n-1]=0,q.push(make_pair(i,n-1));
 33     }
 34     for(int j=1;j<n-1;j++){
 35         if(ditu[0][j]=='0') dis[0][j]=0,q.push(make_pair(0,j));
 36         if(ditu[n-1][j]=='0') dis[n-1][j]=0,q.push(make_pair(n-1,j));
 37     }
 38     while(q.size()){
 39         int px = q.front().first,py = q.front().second;q.pop();
 40         for(int i=0;i<4;i++){
 41             int x =  px + xx[i] , y = py + yy[i];
 42             if(x<0||x>=n||y<0||y>=n||ditu[x][y]=='1') continue;
 43             if(dis[x][y]>dis[px][py]+1){
 44                 vis[x][y] = true;
 45                 dis[x][y]=dis[px][py]+1;
 46                 q.push(make_pair(x,y));
 47             }
 48         }
 49     }
 50     //show();
 51 }
 52 int dis_h(){
 53     int res = 0;
 54     for(int i=0;i<n;i++)
 55         for(int j=0;j<n;j++) if(vis[i][j]){
 56             res = max(res,dis[i][j]);
 57     }
 58     return res;
 59 }
 60 bool IDAstar(int step,int limit){
 61     int h = dis_h();
 62     if(h+step>limit){nextd = min(nextd,h+step);return false;}
 63     if(h==0){
 64         //cout<<step<<endl;
 65         //show();
 66         for(int i=0;i<step;i++){
 67             if(ans[i]==0) puts("east");
 68             else if(ans[i]==1) puts("north");
 69             else if(ans[i]==2) puts("south");
 70             else puts("west");
 71         }
 72         return true;
 73     }
 74     bool visTmp[9][9];
 75     memcpy(visTmp,vis,sizeof visTmp);
 76     for(int cz=0;cz<4;cz++){
 77         memset(vis,false,sizeof vis);
 78         for(int i=0;i<n;i++)
 79         for(int j=0;j<n;j++) if(visTmp[i][j]){
 80             int x = i + xx[cz] , y= j + yy[cz];
 81              if(x<0||x>=n||y<0||y>=n) continue;
 82              if(ditu[x][y]=='1') vis[i][j] = true;
 83              else if(x!=0&&x!=n-1&&y!=0&&y!=n-1) vis[x][y] = true;
 84         }
 85         //cout<<step<<" "<<cz<<endl;
 86         //show();
 87         ans[step] = cz;
 88         if(IDAstar(step+1,limit)) return true;
 89     }
 90     return false;
 91 }
 92 int main()
 93 {
 94     int ca=0;
 95     while(cin>>n){
 96         if(ca++) puts("");
 97         init();
 98         for(int limit = dis_h();;limit=nextd){
 99              bool visTmp[9][9];memcpy(visTmp,vis,sizeof visTmp);
100             nextd = INF;
101             //cout<<"limit:  "<<limit<<endl;
102             if(IDAstar(0,limit)) break;
103             memcpy(vis,visTmp,sizeof vis);
104         }
105         //cout<<endl;
106     }
107     return 0;
108 }

View Code

Tobo or not Tob HDU - 2918

题意：给你一个123456789的3*3玩具，然后你可以按照题目那样旋转，给你一个随机状态和最大步数，问能否在这最大步数以内，将玩具复原，能则回复最小步数，否则-1

算法：康托+bfs预处理或者 IDAStar

思路1：这里可以从123456789bfs向外扩散9步，记录所有状态；这里使用康托展开进行状态压缩；

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 
  9 using namespace std;
 10 
 11 const int INF = 0x3f3f3f3f;
 12 
 13 char num[10];
 14 int limit;
 15 int vis[400000];
 16 
 17 const int fk[10] = {1,1,2,6,24,120,720,5040,40320,362880};
 18 int cantor(int *a){
 19     int ans = 0;
 20     for(int i=0;i<8;i++){
 21         int small = 0;
 22         for(int j=i+1;j<9;j++) if(a[j]<a[i]) small++;
 23         ans += small*fk[8-i];
 24     }
 25     return ans;
 26 }
 27 
 28 void getNum(int x,int (&a)[10]){
 29     for(int i=8;i>=0;i--) a[i] = x%10,x/=10;
 30 }
 31 
 32 struct node{
 33     int a[10],step;
 34 }s;
 35 
 36 void turnA(int (&a)[10]){
 37     int t = a[0];
 38     a[0] = a[3] , a[3] = a[4] , a[4] = a[1] , a[1] = t;
 39 }
 40 void turnA1(int (&a)[10]){
 41     int t = a[0];
 42     a[0] = a[1] , a[1] = a[4] , a[4] = a[3] , a[3] = t;
 43 }
 44 void turnB(int (&a)[10]){
 45     int t = a[1];
 46     a[1] = a[4] , a[4] = a[5] , a[5] = a[2] , a[2] = t;
 47 }
 48 void turnB1(int (&a)[10]){
 49     int t = a[1];
 50     a[1] = a[2] , a[2] = a[5] , a[5] = a[4] , a[4] = t;
 51 }
 52 void turnC(int (&a)[10]){
 53     int t = a[3];
 54     a[3] = a[6] , a[6] = a[7] , a[7] = a[4] , a[4] = t;
 55 }
 56 void turnC1(int (&a)[10]){
 57     int t = a[3];
 58     a[3] = a[4] , a[4] = a[7] , a[7] = a[6] , a[6] = t;
 59 }
 60 void turnD(int (&a)[10]){
 61     int t = a[4];
 62     a[4] = a[5] , a[5] = a[8] , a[8] = a[7] , a[7] = t;
 63 }
 64 void turnD1(int (&a)[10]){
 65     int t = a[4];
 66     a[4] = a[7] , a[7] = a[8] , a[8] = a[5] , a[5] = t;
 67 }
 68 
 69 void init(){
 70     memset(vis,-1,sizeof vis);
 71     int num = 12345678;
 72     getNum(num,s.a);vis[cantor(s.a)] = 0;s.step = 0;
 73     queue<node> q;q.push(s);
 74     while(q.size()){
 75         node p = q.front();q.pop();
 76         if(p.step==9) break;
 77         node u = p;turnA(u.a);int tmp = cantor(u.a);
 78         if(vis[tmp]==-1){vis[tmp] = u.step+1;u.step++;q.push(u);}
 79         u = p;turnA1(u.a);tmp = cantor(u.a);
 80         if(vis[tmp]==-1){vis[tmp] = u.step+1;u.step++;q.push(u);}
 81          u = p;turnB(u.a);tmp = cantor(u.a);
 82         if(vis[tmp]==-1){vis[tmp] = u.step+1;u.step++;q.push(u);}
 83          u = p;turnB1(u.a);tmp = cantor(u.a);
 84         if(vis[tmp]==-1){vis[tmp] = u.step+1;u.step++;q.push(u);}
 85          u = p;turnC(u.a);tmp = cantor(u.a);
 86         if(vis[tmp]==-1){vis[tmp] = u.step+1;u.step++;q.push(u);}
 87          u = p;turnC1(u.a);tmp = cantor(u.a);
 88         if(vis[tmp]==-1){vis[tmp] = u.step+1;u.step++;q.push(u);}
 89          u = p;turnD(u.a);tmp = cantor(u.a);
 90         if(vis[tmp]==-1){vis[tmp] = u.step+1;u.step++;q.push(u);}
 91         u = p;turnD1(u.a);tmp = cantor(u.a);
 92         if(vis[tmp]==-1){vis[tmp] = u.step+1;u.step++;q.push(u);}
 93     }
 94 }
 95 
 96 int main()
 97 {
 98     init();
 99     int ca = 1;
100     while(cin>>num){
101         limit = num[0] - '0';
102         if(limit==0&&num[1]=='0') break;
103         cout<<ca++<<". ";
104         int a[10];
105         for(int i=1;i<10;i++) a[i-1] = num[i] - '0' - 1;
106         int ans = vis[cantor(a)];
107         if(ans>limit) cout<<-1<<endl;
108         else cout<<ans<<endl;
109     }
110     return 0;
111 }

View Code

思路2：这里也可以用IDAstar，启发函数是，与最终状态有多少不同，然后除以4向上取整。

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 #include <math.h>
  9 
 10 using namespace std;
 11 
 12 const int INF = 0x3f3f3f3f;
 13 
 14 char num[10];
 15 int a[10],nextd;
 16 bool vis[400000];
 17 
 18 const int fk[10] = {1,1,2,6,24,120,720,5040,40320,362880};
 19 int cantor(){
 20     int ans = 0;
 21     for(int i=0;i<8;i++){
 22         int small = 0;
 23         for(int j=i+1;j<9;j++) if(a[j]<a[i]) small++;
 24         ans += small*fk[8-i];
 25     }
 26     return ans;
 27 }
 28 void getNum(int x){
 29     for(int i=8;i>=0;i--) a[i] = x%10,x/=10;
 30 }
 31 void turnA(){
 32     int t = a[0];
 33     a[0] = a[3] , a[3] = a[4] , a[4] = a[1] , a[1] = t;
 34 }
 35 void turnA1(){
 36     int t = a[0];
 37     a[0] = a[1] , a[1] = a[4] , a[4] = a[3] , a[3] = t;
 38 }
 39 void turnB(){
 40     int t = a[1];
 41     a[1] = a[4] , a[4] = a[5] , a[5] = a[2] , a[2] = t;
 42 }
 43 void turnB1(){
 44     int t = a[1];
 45     a[1] = a[2] , a[2] = a[5] , a[5] = a[4] , a[4] = t;
 46 }
 47 void turnC(){
 48     int t = a[3];
 49     a[3] = a[6] , a[6] = a[7] , a[7] = a[4] , a[4] = t;
 50 }
 51 void turnC1(){
 52     int t = a[3];
 53     a[3] = a[4] , a[4] = a[7] , a[7] = a[6] , a[6] = t;
 54 }
 55 void turnD(){
 56     int t = a[4];
 57     a[4] = a[5] , a[5] = a[8] , a[8] = a[7] , a[7] = t;
 58 }
 59 void turnD1(){
 60     int t = a[4];
 61     a[4] = a[7] , a[7] = a[8] , a[8] = a[5] , a[5] = t;
 62 }
 63 int dis_h(){
 64     double res = 0;
 65     for(int i=0;i<9;i++) if(a[i]!=i) res++;
 66     return ceil(res/4);
 67 }
 68 
 69 bool IDAstar(int step,int limit){
 70     int h = dis_h();
 71     if(h+step>limit){
 72         nextd = min(nextd,h+step);
 73         return false;
 74     }
 75     if(h==0){
 76         cout<<step<<endl;return true;
 77     }
 78     int tmp;
 79     turnA();tmp=cantor();
 80     if(!vis[tmp]){
 81         vis[tmp]=true;
 82         if(IDAstar(step+1,limit)) return true;
 83         vis[tmp]=false;
 84     }turnA1();
 85     turnA1();tmp=cantor();
 86     if(!vis[tmp]){
 87         vis[tmp]=true;
 88         if(IDAstar(step+1,limit)) return true;
 89         vis[tmp]=false;
 90     }turnA();
 91     turnB();tmp=cantor();
 92     if(!vis[tmp]){
 93         vis[tmp]=true;
 94         if(IDAstar(step+1,limit)) return true;
 95         vis[tmp]=false;
 96     }turnB1();
 97     turnB1();tmp=cantor();
 98     if(!vis[tmp]){
 99         vis[tmp]=true;
100         if(IDAstar(step+1,limit)) return true;
101         vis[tmp]=false;
102     }turnB();
103     turnC();tmp=cantor();
104     if(!vis[tmp]){
105         vis[tmp]=true;
106         if(IDAstar(step+1,limit)) return true;
107         vis[tmp]=false;
108     }turnC1();
109     turnC1();tmp=cantor();
110     if(!vis[tmp]){
111         vis[tmp]=true;
112         if(IDAstar(step+1,limit)) return true;
113         vis[tmp]=false;
114     }turnC();
115     turnD();tmp=cantor();
116     if(!vis[tmp]){
117         vis[tmp]=true;
118         if(IDAstar(step+1,limit)) return true;
119         vis[tmp]=false;
120     }turnD1();
121     turnD1();tmp=cantor();
122     if(!vis[tmp]){
123         vis[tmp]=true;
124         if(IDAstar(step+1,limit)) return true;
125         vis[tmp]=false;
126     }turnD();
127     return false;
128 }
129 
130 int main()
131 {
132     int ca = 1;
133     while(cin>>num){
134         int k = num[0] - '0';
135         if(k==0&&num[1]=='0') break;
136         cout<<ca++<<". ";
137         for(int i=1;i<10;i++) a[i-1] = num[i] - '0' - 1;
138         memset(vis,false,sizeof vis);
139         vis[cantor()]=true;
140         int limit;
141         for(limit = dis_h();limit<=k;limit=nextd){
142             nextd=INF;
143             if(IDAstar(0,limit)) break;
144        }
145         if(limit>k) puts("-1");
146     }
147     return 0;
148 }

View Code

Rubik 2×2×2HDU - 3459

题意：给你一个2*2的2阶魔方，你只能按题目X、Y、Z旋转，给你一个打乱的魔方，你要给出复原的步骤，这里答案不是最小步数亦可。

算法：IDAstar

思路：这里关键就是求每一个面的颜色，左小角的那一块是永远不会动的，所以三个面的颜色，一开始就给出了。然后找其余的7个角，如果一个角存在两个已知颜色，第三个未知颜色一定是与这两个颜色接触的那一面的颜色。这里启发函数，就是先求每个面的不同颜色块总和，然后除以8向上取整。

易错点：就是这里不能判重，会超时，然后注意细节

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 #include <math.h>
  9 
 10 using namespace std;
 11 
 12 const int INF = 0x3f3f3f3f;
 13 
 14 int nextd;
 15 char a[49],color[7];
 16 string ansStr;
 17 
 18 int dis_h(){
 19     int res = 0;
 20     if(a[16]!=color[0]) res++;if(a[17]!=color[0]) res++;if(a[25]!=color[0]) res++;
 21     if(a[34]!=color[1]) res++;if(a[35]!=color[1]) res++;if(a[43]!=color[1]) res++;
 22     if(a[22]!=color[2]) res++;if(a[23]!=color[2]) res++;if(a[30]!=color[2]) res++;
 23     if(a[18]!=color[3]) res++;if(a[19]!=color[3]) res++;if(a[26]!=color[3]) res++;if(a[27]!=color[3]) res++;
 24     if(a[2]!=color[4]) res++;if(a[3]!=color[4]) res++;if(a[10]!=color[4]) res++;if(a[11]!=color[4]) res++;
 25     if(a[20]!=color[5]) res++;if(a[21]!=color[5]) res++;if(a[28]!=color[5]) res++;if(a[29]!=color[5]) res++;
 26     return (res+7)/8;
 27 }
 28 
 29 void turnX(){
 30     int t = a[20]; a[20] = a[21],a[21] = a[29],a[29] = a[28],a[28] = t;
 31     int u = a[3] , v = a[11];a[3] = a[30] ,a[11] = a[22] , a[30] = a[35] ,a[22] = a[43] ,a[35] = a[19] ,a[43] = a[27] ,a[19] = u ,a[27] = v;
 32 }
 33 void Xturn(){
 34     int t = a[20]; a[20] = a[28],a[28] = a[29],a[29] = a[21],a[21] = t;
 35     int u = a[30] , v = a[22];
 36     a[30] = a[3] ,a[22] = a[11] , a[3] = a[19] ,a[11] = a[27] ,a[19] = a[35] ,a[27] = a[43] ,a[35] = u ,a[43] = v;
 37 }
 38 void turnY(){
 39     int t = a[2]; a[2] = a[3],a[3] = a[11],a[11] = a[10],a[10] = t;
 40     int u = a[18] , v = a[19];
 41     a[18] = a[16] ,a[19] = a[17] , a[16] = a[22] ,a[17] = a[23] ,a[22] = a[20] ,a[23] = a[21] ,a[20] = u ,a[21] = v;
 42 }
 43 void Yturn(){
 44     int t = a[2]; a[2] = a[10],a[10] = a[11],a[11] = a[3],a[3] = t;
 45     int u = a[18] , v = a[19];
 46     a[18] = a[20] ,a[19] = a[21] , a[20] = a[22] ,a[21] = a[23] ,a[22] = a[16] ,a[23] = a[17] ,a[16] = u ,a[17] = v;
 47 }
 48 void turnZ(){
 49     int t = a[18]; a[18] = a[19],a[19] = a[27],a[27] = a[26],a[26] = t;
 50     int u = a[20] , v = a[28];
 51     a[20] = a[35] ,a[28] = a[34] , a[35] = a[25] ,a[34] = a[17] ,a[25] = a[10] ,a[17] = a[11] ,a[10] = u ,a[11] = v;
 52 }
 53 void Zturn(){
 54     int t = a[18]; a[18] = a[26],a[26] = a[27],a[27] = a[19],a[19] = t;
 55     int u = a[20] , v = a[28];
 56     a[20] = a[10] ,a[28] = a[11] , a[10] = a[25] ,a[11] = a[17] ,a[25] = a[35] ,a[17] = a[34] ,a[35] = u ,a[34] = v;
 57 }
 58 
 59 char getColor(char x,char y){
 60     if(a[17]==x&&a[18]==y) return a[10];if(a[17]==x&&a[10]==y) return a[18];if(a[10]==x&&a[18]==y) return a[17];
 61     if(a[17]==y&&a[18]==x) return a[10];if(a[17]==y&&a[10]==x) return a[18];if(a[10]==y&&a[18]==x) return a[17];
 62 
 63     if(a[25]==x&&a[26]==y) return a[34];if(a[25]==x&&a[34]==y) return a[26];if(a[26]==x&&a[34]==y) return a[25];
 64     if(a[25]==y&&a[26]==x) return a[34];if(a[25]==y&&a[34]==x) return a[26];if(a[26]==y&&a[34]==x) return a[25];
 65 
 66     if(a[11]==x&&a[19]==y) return a[20];if(a[11]==x&&a[20]==y) return a[19];if(a[19]==x&&a[20]==y) return a[11];
 67     if(a[11]==y&&a[19]==x) return a[20];if(a[11]==y&&a[20]==x) return a[19];if(a[19]==y&&a[20]==x) return a[11];
 68 
 69     if(a[27]==x&&a[28]==y) return a[35];if(a[27]==x&&a[35]==y) return a[28];if(a[28]==x&&a[35]==y) return a[27];
 70     if(a[27]==y&&a[28]==x) return a[35];if(a[27]==y&&a[35]==x) return a[28];if(a[28]==y&&a[35]==x) return a[27];
 71 
 72     if(a[16]==x&&a[2]==y) return a[23];if(a[16]==x&&a[23]==y) return a[2];if(a[23]==x&&a[2]==y) return a[16];
 73     if(a[16]==y&&a[2]==x) return a[23];if(a[16]==y&&a[23]==x) return a[2];if(a[23]==y&&a[2]==x) return a[16];
 74 
 75     if(a[43]==y&&a[29]==x) return a[30];if(a[43]==y&&a[30]==x) return a[29];if(a[29]==y&&a[30]==x) return a[43];
 76     if(a[43]==x&&a[29]==y) return a[30];if(a[43]==x&&a[30]==y) return a[29];if(a[29]==x&&a[30]==y) return a[43];
 77 
 78     if(a[3]==y&&a[21]==x) return a[22];if(a[3]==y&&a[22]==x) return a[21];if(a[21]==y&&a[22]==x) return a[3];
 79     if(a[3]==x&&a[21]==y) return a[22];if(a[3]==x&&a[22]==y) return a[21];if(a[21]==x&&a[22]==y) return a[3];
 80 }
 81 
 82 bool IDAstar(int step,int limit){
 83     int h = dis_h();
 84     if(h+step>limit){nextd=min(nextd,h+step);return false;}
 85     if(h==0){cout<<ansStr<<endl;return true;}
 86     string tmpStr = ansStr;
 87 
 88     turnX();
 89     ansStr+='X';
 90     if(IDAstar(step+1,limit)) return true;
 91     ansStr = tmpStr;
 92     Xturn();
 93 
 94     turnY();
 95     ansStr+='Y';
 96     if(IDAstar(step+1,limit)) return true;
 97     ansStr = tmpStr;
 98     Yturn();
 99 
100     turnZ();
101     ansStr+='Z';
102     if(IDAstar(step+1,limit)) return true;
103     ansStr = tmpStr;
104     Zturn();
105 
106     return false;
107 }
108 
109 int main()
110 {
111     while(1){
112         for(int i=0;i<48;i++){
113             char ch=getchar();while(ch==' '||ch=='\n') ch=getchar();
114             a[i]=ch;
115         } a[48]='\0';
116         if(a[2]=='.') break;
117         color[0] = a[24],color[1] = a[42], color[2]  = a[31];
118         color[3] = getColor(color[0],color[1]);
119         color[4] = getColor(color[0],color[2]);
120         color[5] = getColor(color[1],color[2]);
121         //-----------------------------------------------------
122         for(int limit = dis_h();;limit=nextd){
123             ansStr="";nextd=INF;
124             if(IDAstar(0,limit)) break;
125         }
126     }
127 }

View Code

Rubiks Cube HDU - 2953

题意：给你一个2*2*2的2阶魔方，问复原所需要最小步数？

算法：bfs预处理+bfs（双向BFS）

思路：这题和上题Rubik 2×2×2HDU - 3459思路差不多，但是这题使用IDAstar会TLE，因为用例有100，且只有1s；

　　　2阶魔方，有一个独特之处，在于，你只需要想上面那样操作3个面就行，你这个面的顺时针就相当于反面逆时针，所以操作只要像上一题一样，多加一个逆时针操作。

　　　并且也和上一题那样，确定颜色。

　　　然后预处理BFS，先存从终点OOOORRGGBBWWRRGGBBWWYYYY向外BFS七步的所有状态；再然后，再确定颜色之后，按照这个最终颜色来改变颜色，再正向BFS，求步数，如果中途，遇到所存状态，可以直接输出。

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 #include <math.h>
  9 
 10 using namespace std;
 11 
 12 const int INF = 0x3f3f3f3f;
 13 
 14 int nextd,ans;
 15 char a[25],color[7];
 16 map<string,int> mp;
 17 
 18 struct node{
 19     char a[25];int step;
 20     node(char b[25],int c){
 21         memcpy(a,b,sizeof a);
 22         step = c;
 23     }
 24 };
 25 
 26 void turnXX(char (&a)[25]){
 27     int t = a[6]; a[6] = a[7],a[7] = a[15],a[15] = a[14],a[14] = t;
 28     int u = a[1] , v = a[3];a[1] = a[16] ,a[3] = a[8] , a[16] = a[21] ,a[8] = a[23] ,a[21] = a[5] ,a[23] = a[13] ,a[5] = u ,a[13] = v;
 29 }
 30 void XXturn(char (&a)[25]){
 31     int t = a[6]; a[6] = a[14],a[14] = a[15],a[15] = a[7],a[7] = t;
 32     int u = a[16] , v = a[8];
 33     a[16] = a[1] ,a[8] = a[3] , a[1] = a[5] ,a[3] = a[13] ,a[5] = a[21] ,a[13] = a[23] ,a[21] = u ,a[23] = v;
 34 }
 35 void turnYY(char (&a)[25]){
 36     int t = a[0]; a[0] = a[1],a[1] = a[3],a[3] = a[2],a[2] = t;
 37     int u = a[4] , v = a[5];
 38     a[4] = a[10] ,a[5] = a[11] , a[10] = a[8] ,a[11] = a[9] ,a[8] = a[6] ,a[9] = a[7] ,a[6] = u ,a[7] = v;
 39 }
 40 void YYturn(char (&a)[25]){
 41     int t = a[0]; a[0] = a[2],a[2] = a[3],a[3] = a[1],a[1] = t;
 42     int u = a[4] , v = a[5];
 43     a[4] = a[6] ,a[5] = a[7] , a[6] = a[8] ,a[7] = a[9] ,a[8] = a[10] ,a[9] = a[11] ,a[10] = u ,a[11] = v;
 44 }
 45 void turnZZ(char (&a)[25]){
 46     int t = a[4]; a[4] = a[5],a[5] = a[13],a[13] = a[12],a[12] = t;
 47     int u = a[6] , v = a[14];
 48     a[6] = a[21] ,a[14] = a[20] , a[21] = a[19] ,a[20] = a[11] ,a[19] = a[2] ,a[11] = a[3] ,a[2] = u ,a[3] = v;
 49 }
 50 void ZZturn(char (&a)[25]){
 51     int t = a[4]; a[4] = a[12],a[12] = a[13],a[13] = a[5],a[5] = t;
 52     int u = a[6] , v = a[14];
 53     a[6] = a[2] ,a[14] = a[3] , a[2] = a[19] ,a[3] = a[11] ,a[19] = a[21] ,a[11] = a[20] ,a[21] = u ,a[20] = v;
 54 }
 55 
 56 void bfs(){
 57     queue<node> q;
 58     char ch[25]={"OOOORRGGBBWWRRGGBBWWYYYY"};ch[24]='\0';
 59     mp[ch]=0;
 60     q.push(node(ch,0));
 61     while(q.size()){
 62         node p = q.front();q.pop();
 63         int step = p.step+1;
 64 
 65         node u = p;XXturn(u.a);
 66         if(mp.find(u.a)==mp.end()){
 67             mp[u.a]=step;
 68             if(step<7) u.step++,q.push(u);
 69         }
 70         u = p;turnXX(u.a);
 71         if(mp.find(u.a)==mp.end()){
 72             mp[u.a]=step;
 73             if(step<7) u.step++,q.push(u);
 74         }
 75         u = p;YYturn(u.a);
 76         if(mp.find(u.a)==mp.end()){
 77             mp[u.a]=step;
 78             if(step<7) u.step++,q.push(u);
 79         }
 80         u = p;turnYY(u.a);
 81         if(mp.find(u.a)==mp.end()){
 82             mp[u.a]=step;
 83             if(step<7) u.step++,q.push(u);
 84         }
 85         u = p;ZZturn(u.a);
 86         if(mp.find(u.a)==mp.end()){
 87             mp[u.a]=step;
 88             if(step<7) u.step++,q.push(u);
 89         }
 90         u = p;turnZZ(u.a);
 91         if(mp.find(u.a)==mp.end()){
 92             mp[u.a]=step;
 93             if(step<7) u.step++,q.push(u);
 94         }
 95     }
 96 }
 97 
 98 char getColor(char x,char y){
 99     if(a[11]==x&&a[4]==y) return a[2];if(a[11]==x&&a[2]==y) return a[4];if(a[2]==x&&a[4]==y) return a[11];
100     if(a[11]==y&&a[4]==x) return a[2];if(a[11]==y&&a[2]==x) return a[4];if(a[2]==y&&a[4]==x) return a[11];
101 
102     if(a[19]==x&&a[12]==y) return a[20];if(a[19]==x&&a[20]==y) return a[12];if(a[12]==x&&a[20]==y) return a[19];
103     if(a[19]==y&&a[12]==x) return a[20];if(a[19]==y&&a[20]==x) return a[12];if(a[12]==y&&a[20]==x) return a[19];
104 
105     if(a[13]==x&&a[14]==y) return a[21];if(a[13]==x&&a[21]==y) return a[14];if(a[14]==x&&a[21]==y) return a[13];
106     if(a[13]==y&&a[14]==x) return a[21];if(a[13]==y&&a[21]==x) return a[14];if(a[14]==y&&a[21]==x) return a[13];
107 
108     if(a[3]==x&&a[5]==y) return a[6];if(a[3]==x&&a[6]==y) return a[5];if(a[5]==x&&a[6]==y) return a[3];
109     if(a[3]==y&&a[5]==x) return a[6];if(a[3]==y&&a[6]==x) return a[5];if(a[5]==y&&a[6]==x) return a[3];
110 
111     if(a[10]==x&&a[0]==y) return a[9];if(a[9]==x&&a[10]==y) return a[0];if(a[0]==x&&a[9]==y) return a[10];
112     if(a[10]==y&&a[0]==x) return a[9];if(a[9]==y&&a[10]==x) return a[0];if(a[0]==y&&a[9]==x) return a[10];
113 
114     if(a[23]==y&&a[15]==x) return a[16];if(a[23]==y&&a[16]==x) return a[15];if(a[15]==y&&a[16]==x) return a[23];
115     if(a[23]==x&&a[15]==y) return a[16];if(a[23]==x&&a[16]==y) return a[15];if(a[15]==x&&a[16]==y) return a[23];
116 
117     if(a[1]==y&&a[7]==x) return a[8];if(a[1]==y&&a[8]==x) return a[7];if(a[7]==y&&a[8]==x) return a[1];
118     if(a[1]==x&&a[7]==y) return a[8];if(a[1]==x&&a[8]==y) return a[7];if(a[7]==x&&a[8]==y) return a[1];
119 }
120 //OOOORRGGBBWWRRGGBBWWYYYY
121 void changeColor(){
122     for(int i=0;i<24;i++){
123         if(a[i]==color[0]) a[i]='W';
124         else if(a[i]==color[1]) a[i]='Y';
125         else if(a[i]==color[2]) a[i]='B';
126         else if(a[i]==color[3]) a[i]='R';
127         else if(a[i]==color[4]) a[i]='O';
128         else a[i]='G';
129     }
130 }
131 
132 void bfs2(){
133     queue<node> q;
134     map<string,bool> vis;
135     vis[a] = true;
136     q.push(node(a,0));
137     while(q.size()){
138         node p = q.front();q.pop();
139 
140         if(mp.find(p.a)!=mp.end()){
141             cout<<p.step+mp[p.a]<<endl;
142             break;
143         }
144 
145         node u = p;XXturn(u.a);
146         if(!vis[u.a]) vis[u.a]=true,u.step++,q.push(u);
147         u = p;turnXX(u.a);
148         if(!vis[u.a]) vis[u.a]=true,u.step++,q.push(u);
149         u = p;YYturn(u.a);
150         if(!vis[u.a]) vis[u.a]=true,u.step++,q.push(u);
151         u = p;turnYY(u.a);
152         if(!vis[u.a]) vis[u.a]=true,u.step++,q.push(u);
153         u = p;ZZturn(u.a);
154         if(!vis[u.a]) vis[u.a]=true,u.step++,q.push(u);
155         u = p;turnZZ(u.a);
156         if(!vis[u.a]) vis[u.a]=true,u.step++,q.push(u);
157 
158     }
159 }
160 
161 int main()
162 {
163     bfs();
164     int _;cin>>_;
165     while(_--){
166         for(int i=0;i<24;i++){
167             char ch=getchar();while(ch==' '||ch=='\n') ch=getchar();
168             a[i]=ch;
169         } a[24]='\0';
170         //-----------------------------------------------------
171         color[0] = a[18],color[1] = a[22], color[2]  = a[17];
172         color[3] = getColor(color[0],color[1]);
173         color[4] = getColor(color[0],color[2]);
174         color[5] = getColor(color[1],color[2]);
175         changeColor();
176         bfs2();
177     }
178 }

View Code

2-Dimensional Rubik's Cube HDU - 2691

题意：同样是2阶魔方，然后给出两个状态，问状态1到状态2最少需要多少步？（一定有解）

算法：双向BFS+状压

思路：这里IDAStar同样会TLE，然后队列节点不进行数组压缩成一个LongLong的话，会MLE，因为这里一定有解，所以双向BFS，不需要分层来寻找答案。

易错点：注意细节、然后要状态压缩

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 #include <math.h>
  9 
 10 using namespace std;
 11 
 12 const int INF = 0x3f3f3f3f;
 13 
 14 int nextd;
 15 int a[25],b[25];
 16 int face[6][4]={{0,1,3,2},{4,5,13,12},{6,7,15,14},{8,9,17,16},{10,11,19,18},{20,21,23,22}};
 17 int faceX[6][4]={{10,8,6,4},{0,6,20,19},{2,8,21,13},{3,10,23,15},{1,4,22,17},{14,16,18,12}};
 18 int faceY[6][4]={{11,9,7,5},{2,14,22,11},{3,16,20,5},{1,18,21,7},{0,12,23,9},{15,17,19,13}};
 19 
 20 void turn(int x,int flag,int (&a)[25]){
 21     if(flag){
 22         int tmp = a[face[x][0]];for(int i=0;i<3;i++) a[face[x][i]] =a[face[x][i+1]];a[face[x][3]] = tmp;
 23         tmp = a[faceX[x][0]];for(int i=0;i<3;i++) a[faceX[x][i]] =a[faceX[x][i+1]];a[faceX[x][3]] = tmp;
 24         tmp = a[faceY[x][0]];for(int i=0;i<3;i++) a[faceY[x][i]] =a[faceY[x][i+1]];a[faceY[x][3]] = tmp;
 25     }else{
 26         int tmp = a[face[x][3]];for(int i=3;i>0;i--) a[face[x][i]] =a[face[x][i-1]];a[face[x][0]] = tmp;
 27         tmp = a[faceX[x][3]];for(int i=3;i>0;i--) a[faceX[x][i]] =a[faceX[x][i-1]];a[faceX[x][0]] = tmp;
 28         tmp = a[faceY[x][3]];for(int i=3;i>0;i--) a[faceY[x][i]] =a[faceY[x][i-1]];a[faceY[x][0]] = tmp;
 29     }
 30 }
 31 
 32 void init(){
 33     for(int i=0;i<24;i++){
 34         char ch=getchar();while(ch==' '||ch=='\n') ch=getchar();
 35         if(ch=='O') a[i] = 0;
 36         else if(ch=='R') a[i] = 1;
 37         else if(ch=='G') a[i] = 2;
 38         else if(ch=='B') a[i] = 3;
 39         else if(ch=='W') a[i] = 4;
 40         else a[i] = 5;
 41     }
 42     for(int i=0;i<24;i++){
 43         char ch=getchar();while(ch==' '||ch=='\n') ch=getchar();
 44         if(ch=='O') b[i] = 0;
 45         else if(ch=='R') b[i] = 1;
 46         else if(ch=='G') b[i] = 2;
 47         else if(ch=='B') b[i] = 3;
 48         else if(ch=='W') b[i] = 4;
 49         else b[i] = 5;
 50     }
 51     //for(int i=0;i<24;i++) cout<<a[i]<<" ";cout<<endl;
 52 }
 53 
 54 struct node{
 55     long long a;int step;
 56     node(int b[25],int c){
 57         a = b[0];
 58         for(int i=1;i<24;i++) a*=6,a+=b[i];
 59         step = c;
 60     }
 61     void makeSZ(int (&b)[25]){
 62         long long x =a ;
 63         for(int i=23;i>=0;i--){
 64             b[i] = (int)( x % 6); x = x / 6;
 65         }
 66     }
 67 };
 68 
 69 int solve(){
 70     queue<node> q1,q2;
 71     map<long long,int> vis1,vis2;
 72     node s = node(a,0) , t = node(b,0);
 73     vis1[s.a]=0;vis2[t.a]=0;
 74     q1.push(s);q2.push(t);
 75     int step=0;
 76     while(q1.size()&&q2.size()){
 77 
 78         while(q1.size()){
 79             node p1 = q1.front();
 80             if(vis2.find(p1.a)!=vis2.end()) return p1.step+vis2[p1.a];
 81             if(p1.step>step) break;
 82             else q1.pop();
 83             for(int i=0;i<6;i++){
 84                 for(int j=0;j<2;j++){
 85                     int tmp[25];
 86                     p1.makeSZ(tmp);
 87                     turn(i,j,tmp);
 88                     node u = node(tmp,p1.step+1);
 89                      if(vis2.find(u.a)!=vis2.end()) return u.step+vis2[u.a];
 90                      if(vis1.find(u.a)!=vis1.end()) continue;
 91                      vis1[u.a]=u.step;
 92                      q1.push(u);
 93                 }
 94             }
 95         }
 96  //----------------------------------------------------------------------
 97         while(q2.size()){
 98             node p2 = q2.front();
 99             if(vis1.find(p2.a)!=vis1.end()) return p2.step+vis1[p2.a];
100             if(p2.step>step) break;
101             else q2.pop();
102             for(int i=0;i<6;i++){
103                 for(int j=0;j<2;j++){
104                     int tmp[25];
105                     p2.makeSZ(tmp);
106                     turn(i,j,tmp);
107                     node u = node(tmp,p2.step+1);
108                      if(vis1.find(u.a)!=vis1.end()) return u.step+vis1[u.a];
109                      if(vis2.find(u.a)!=vis2.end()) continue;
110                      vis2[u.a]=u.step;
111                      q2.push(u);
112                 }
113             }
114         }
115         step++;
116     }
117     return -1;
118 }
119 
120 int main()
121 {
122     int _;cin>>_;
123     while(_--){
124         init();
125         cout<<solve()<<endl;
126     }
127 }

View Code

上面：两个队列分别一层层出下面：两个队列一个个的出

  1 #include <iostream>
  2 #include <vector>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <queue>
  6 #include <cstdio>
  7 #include <map>
  8 #include <math.h>
  9 
 10 using namespace std;
 11 
 12 const int INF = 0x3f3f3f3f;
 13 
 14 int nextd;
 15 int a[25],b[25];
 16 int face[6][4]={{0,1,3,2},{4,5,13,12},{6,7,15,14},{8,9,17,16},{10,11,19,18},{20,21,23,22}};
 17 int faceX[6][4]={{10,8,6,4},{0,6,20,19},{2,8,21,13},{3,10,23,15},{1,4,22,17},{14,16,18,12}};
 18 int faceY[6][4]={{11,9,7,5},{2,14,22,11},{3,16,20,5},{1,18,21,7},{0,12,23,9},{15,17,19,13}};
 19 
 20 void turn(int x,int flag,int (&a)[25]){
 21     if(flag){
 22         int tmp = a[face[x][0]];for(int i=0;i<3;i++) a[face[x][i]] =a[face[x][i+1]];a[face[x][3]] = tmp;
 23         tmp = a[faceX[x][0]];for(int i=0;i<3;i++) a[faceX[x][i]] =a[faceX[x][i+1]];a[faceX[x][3]] = tmp;
 24         tmp = a[faceY[x][0]];for(int i=0;i<3;i++) a[faceY[x][i]] =a[faceY[x][i+1]];a[faceY[x][3]] = tmp;
 25     }else{
 26         int tmp = a[face[x][3]];for(int i=3;i>0;i--) a[face[x][i]] =a[face[x][i-1]];a[face[x][0]] = tmp;
 27         tmp = a[faceX[x][3]];for(int i=3;i>0;i--) a[faceX[x][i]] =a[faceX[x][i-1]];a[faceX[x][0]] = tmp;
 28         tmp = a[faceY[x][3]];for(int i=3;i>0;i--) a[faceY[x][i]] =a[faceY[x][i-1]];a[faceY[x][0]] = tmp;
 29     }
 30 }
 31 
 32 void init(){
 33     for(int i=0;i<24;i++){
 34         char ch=getchar();while(ch==' '||ch=='\n') ch=getchar();
 35         if(ch=='O') a[i] = 0;
 36         else if(ch=='R') a[i] = 1;
 37         else if(ch=='G') a[i] = 2;
 38         else if(ch=='B') a[i] = 3;
 39         else if(ch=='W') a[i] = 4;
 40         else a[i] = 5;
 41     }
 42     for(int i=0;i<24;i++){
 43         char ch=getchar();while(ch==' '||ch=='\n') ch=getchar();
 44         if(ch=='O') b[i] = 0;
 45         else if(ch=='R') b[i] = 1;
 46         else if(ch=='G') b[i] = 2;
 47         else if(ch=='B') b[i] = 3;
 48         else if(ch=='W') b[i] = 4;
 49         else b[i] = 5;
 50     }
 51     //for(int i=0;i<24;i++) cout<<a[i]<<" ";cout<<endl;
 52 }
 53 
 54 struct node{
 55     long long a;int step;
 56     node(int b[25],int c){
 57         a = b[0];
 58         for(int i=1;i<24;i++) a*=6,a+=b[i];
 59         step = c;
 60     }
 61     void makeSZ(int (&b)[25]){
 62         long long x =a ;
 63         for(int i=23;i>=0;i--){
 64             b[i] = (int)( x % 6); x = x / 6;
 65         }
 66     }
 67 };
 68 
 69 int solve(){
 70     queue<node> q1,q2;
 71     map<long long,int> vis1,vis2;
 72     node s = node(a,0) , t = node(b,0);
 73     vis1[s.a]=0;vis2[t.a]=0;
 74     q1.push(s);q2.push(t);
 75     while(q1.size()&&q2.size()){
 76 
 77             node p1 = q1.front();q1.pop();
 78             if(vis2.find(p1.a)!=vis2.end()) return p1.step+vis2[p1.a];
 79 
 80             for(int i=0;i<6;i++){
 81                 for(int j=0;j<2;j++){
 82                     int tmp[25];
 83                     p1.makeSZ(tmp);
 84                     turn(i,j,tmp);
 85                     node u = node(tmp,p1.step+1);
 86                      if(vis2.find(u.a)!=vis2.end()) return u.step+vis2[u.a];
 87                      if(vis1.find(u.a)!=vis1.end()) continue;
 88                      vis1[u.a]=u.step;
 89                      q1.push(u);
 90                 }
 91             }
 92  //----------------------------------------------------------------------
 93             node p2 = q2.front();q2.pop();
 94             if(vis1.find(p2.a)!=vis1.end()) return p2.step+vis1[p2.a];
 95 
 96             for(int i=0;i<6;i++){
 97                 for(int j=0;j<2;j++){
 98                     int tmp[25];
 99                     p2.makeSZ(tmp);
100                     turn(i,j,tmp);
101                     node u = node(tmp,p2.step+1);
102                      if(vis1.find(u.a)!=vis1.end()) return u.step+vis1[u.a];
103                      if(vis2.find(u.a)!=vis2.end()) continue;
104                      vis2[u.a]=u.step;
105                      q2.push(u);
106                 }
107             }
108 
109     }
110     return -1;
111 }
112 
113 int main()
114 {
115     int _;cin>>_;
116     while(_--){
117         init();
118         cout<<solve()<<endl;
119     }
120 }

View Code

Déjà vuHDU - 2467

题意：N：表面数字都在(0~2^N-1)内，N最大20；M：0~2^N-1内不同的正整数，并且二进制都只有3个1，（这里因为不同，所以1的位置排列也不同）；S一个初始状态，T一个最终状态；问是否存在多个M数实现公式 S^M1^M2^M3^...=T?

算法：IDAstar

思路：1.这里公式可以左右两边都异或S，就变成M1^M2^M3^……=T^S,然后继续异或：M2^M3^……=T^S^M1,最终会变成 0 = T^S^M1^M2^……；公式左边会变成0；所以每次选举一个M出来异或就行，再者这里是异或操作，所以一个数只能异或一次，那么它在公式里状态只能是存在或者不存在；所以IDAstar向下枚举可以随着id，循环减少；

　　 2.这里启发函数维护一个，当前状态，剩余多少个二进制状态1，没有消除，因为最后要变成0才算成功。一开始是觉得一次操作，一个数可以消除3个1，所以就除以3向上取整了，不出意味TLE了，这里异或，所以这样不行，就一个个手算出来，因为只有20位，所以cnt数组：int cnt[]={0,3,2,1,2,3,2,3,4,3,4,5,4,5,6,5,6,7,6,7,8}; 当剩余0个1，不需要操作；剩余1个1，则至少需要3次操作；以此类推。

　　3.这里有个优化，可以事先预处理，0~2^N-1里面的数，二进制有多少个1；

　　4.这里只有20位个1，理想情况下，不能存在无效消除1的情况，所以limit最大20

 1 #include <iostream>
 2 #include <vector>
 3 #include <cstring>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <cstdio>
 7 #include <map>
 8 #include <math.h>
 9 
10 using namespace std;
11 
12 const int INF = 0x3f3f3f3f;
13 
14 int n,m,S,T,ans,nextd;
15 int num[1<<20];
16 int res[1<<20];
17 int cnt[]={0,3,2,1,2,3,2,3,4,3,4,5,4,5,6,5,6,7,6,7,8};
18 
19 int dis_h(int x){
20     return cnt[res[x]];
21 }
22 
23 bool IDAstar(int x,int step,int id,int limit){
24     int h = dis_h(x);
25     if(h+step>limit){
26         nextd = min(nextd , h+step);return false;
27     }
28     if(h==0) {ans = step;return true;}
29     for(int i=id;i<m;i++) if(IDAstar(x^num[i],step+1,i+1,limit)) return true;
30     return false;
31 }
32 
33 int main()
34 {
35     res[0]=0;
36     for(int i=1;i<(1<<20);i++) res[i] = res[i>>1] + (i&1);
37     int cas = 1;
38     while(cin>>n>>m&&n&&m){
39         cin>>S>>T;
40         for(int i=0;i<m;i++) cin>>num[i];
41         int num  = S^T,f = min(20,m);ans = INF;
42         for(int limit = dis_h(num);limit<=f;limit=nextd){
43             nextd = INF;
44             if(IDAstar(num,0,0,limit)) break;
45         }
46         cout<<"Case #"<<cas++<<": ";
47         if(ans==INF) puts("Impossible");
48         else cout<<ans<<endl;
49     }
50 }

View Code

Destroying the bus stationsHDU - 2485

题意：给你一个n个点巴士站，单向边，每条边只需1分钟车程，军队车会从巴士站1出发，最终到达n点，问你至少要炸毁多少个车站，才能让军队不在K分钟内到达n点？？

算法：网络流：最大流/最小割、最小费用最大流问题

这题，我知道是网络流，但是我还没学到，也不想半懂半解的解决它，等我学完再回来补吧。

学完回来补了，网路流的最大流问题、最小割问题，最小费用最大流问题。算法学习：https://zhuanlan.zhihu.com/p/617967342

最大流问题就是图每个路径都有流通容量，即这条路流过这个量就不能再通过了，问从源点到底最多可以流多少水到汇点？？；

最小割问题就是问割去一些边使得汇点源点不相通的情况下，这些边的总容量和最小？？这里最小割问题其实就是最大流问题（这个我就不解释了。）

最小费用最大流，其实就是每个边增加一个代价，即过路费，问在保持最大流情况下，路径总费用最少？

思路：这题刚好涉及到这三个东西；首先最小割是割边，而这里是割点，我们其实可以把点拆分成两个，然后两个点构造一个边，边容量为1（即这个点只用删一次，最后最大流就表示要删多少次这种边，即删多少个点），其他边容量为INF（这里题目巴士可以无限次走这条路所以是INF），巧妙地把最小割点变成最小割问题。

解法1：最小割问题，是使得s、t点不连通，而这题是，使得到达t点的时间大于K，这里思维转换一下，如果我们只保留时间小于等于K的路径，再求最小割（最大流）不就是答案了吗？预处理一下，从s点跑一次spfa，得到dis1【i】——这个点到s的距离；用反向边从t点跑一次是spafa,得到dis2【i】——这个点到t的距离。然后对每个存在的边（u，v）进行判断——dis1[u]+dis2[v]+1>k——这个边就不要进图了。构建完图之后，跑一次最大流就是答案。

解法2：这里用最小费用最大流，拆点之后的内边费用为0——因为点自己内部走不需要费用，其他边费用为1；因为最小费用，已经维护了一个最短路径，然后我们只要在循环spfa到汇点的费用大于K的时候中止，这之前的最大流与解法1同理。

注意：这里s、t点不能炸，所以不能拆点。而且也不合理。

最大流

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string.h>
#include <queue>
#include <vector>
#include <stack>
#include <cmath>
#include <map>
#include <limits.h>
#include <float.h>

#define sc scanf
#define pf printf
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define CLR(x,m) memset(x,m,sizeof x);
#define LOCAL freopen("test.txt","r",stdin)
#define UCCU ios::sync_with_stdio(0);
#define XSD(i) cout << fixed << setprecision(i);
#define pii pair<int,int>
#define xx first
#define yy second

using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef double DB;
typedef long double LDB;

const double eps = 1e-8;
//const int inf = 1<<30;
const int INF = 0x3f3f3f3f;
const long long llinf = (long long)300100*1000000000;
const DB PI = acos(-1.0);
const LL mod = 1e9+7;

//-----------------------------------------------------------------------
const int MAXN = 100 + 10;
const int MAXM = 8100 + 10;
struct Edge{
    int to,next,cap,flow;
}edge[MAXM];
int tol,head[MAXN];
void init(){
    tol = 2;
    memset(head, -1, sizeof head);
}
void addedge(int u,int v,int w,int rw = 0){
    edge[tol].to = v;edge[tol].cap = w;edge[tol].flow = 0;
    edge[tol].next = head[u];head[u] = tol++;
    edge[tol].to = u;edge[tol].cap = rw;edge[tol].flow = 0;
    edge[tol].next = head[v];head[v] = tol++;
}
int Q[MAXN];
int dep[MAXN],cur[MAXN],sta[MAXN];
bool bfs(int s,int t,int n){
    int front = 0,tail = 0;
    memset(dep, -1, sizeof(dep[0])*(n+n+1));
    dep[s] = 0;
    Q[tail++] = s;
    while(front < tail){
        int u = Q[front++];
        for(int i = head[u];i != -1;i = edge[i].next){
            int v = edge[i].to;
            if(edge[i].cap > edge[i].flow && dep[v] == -1){
                dep[v] = dep[u] + 1;
                if(v == t) return true;
                Q[tail++] = v;
            }
        }
    }
    return false;
}
int dinic(int s,int t,int n){
    int maxflow = 0;
    while(bfs(s,t,n)){
        for(int i=0;i<n+n;i++) cur[i] = head[i];
        int u = s,tail = 0;
        while(cur[s] != -1){
            if(u == t){
                int tp = INF;
                for(int i=tail-1;i>=0;i--) tp = min(tp, edge[sta[i]].cap-edge[sta[i]].flow);
                maxflow+=tp;
                for(int i=tail-1;i>=0;i--){
                    edge[sta[i]].flow+=tp;
                    edge[sta[i]^1].flow-=tp;
                    if(edge[sta[i]].cap-edge[sta[i]].flow==0) tail = i;
                }
                u = edge[sta[tail]^1].to;
            }else if(cur[u] != -1 && edge[cur[u]].cap > edge[cur[u]].flow && dep[u] +1 ==dep[edge[cur[u]].to]){
                sta[tail++] = cur[u];
                u = edge[cur[u]].to;
            }else{
                while(u != s && cur[u] == -1) u = edge[sta[--tail]^1].to;
                cur[u] = edge[cur[u]].next;
            }
        }
    }
    return maxflow;
}

int n,m,k;
vector<int> E1[MAXN],E2[MAXN];
int dis1[MAXN],dis2[MAXN];
bool vis1[MAXN],vis2[MAXN];
void SPFA(int start,int n,int (&dis)[MAXN],bool vis[MAXN],vector<int> E[MAXN]){
    vis[start]=true,dis[start]=0;
    queue<int> q;q.push(start);
    while(q.size()){
        int u = q.front();q.pop();
        vis[u]=false;
        for(int i=0;i<E[u].size();i++){
            int v = E[u][i];
            if(dis[v]>dis[u]+1){
                dis[v]=dis[u]+1;
                if(!vis[v]){
                    vis[v] = true;
                    q.push(v);
                }
            }
        }
    }
}
void init_2(){
    bool ee[MAXN][MAXN];
    memset(ee,false,sizeof ee);
    for(int i=0;i<n;i++){
        E1[i].clear();E2[i].clear();
        dis1[i] = INF;dis2[i] = INF;
        vis1[i] = false;vis2[i] = false;
    }
    while(m--){
        int a,b;cin>>a>>b;
        E1[a-1].push_back(b-1);
        E2[b-1].push_back(a-1);
        ee[a-1][b-1] = true;
    }
    SPFA(0,n,dis1,vis1,E1);
    SPFA(n-1,n,dis2,vis2,E2);
    //puts("=============");
    for(int i=0;i<n;i++){
        if(i!=0&&i!=n-1) addedge(i,i+n,1);
        for(int j=0;j<n;j++){
            if(i==j||!ee[i][j]) continue;
            if(dis1[i]+dis2[j]+1>k) continue;
            //cout<<i<<" "<<j<<endl;
            if(i!=0&&i!=n-1) addedge(i+n,j,INF);
            else addedge(i,j,INF);
        }
    }
}

int main(){
    while(cin>>n>>m>>k&&n&&m&&k){
        init();
        init_2();
        cout<<dinic(0,n-1,n)<<endl;
    }
    return 0;
}

最小费用最大流

 #include <iostream>
#include <cstdio>
#include <cstring>
#include <string.h>
#include <queue>
#include <vector>
#include <stack>
#include <cmath>
#include <map>
#include <limits.h>
#include <float.h>

#define sc scanf
#define pf printf
#define REP(i,a,b) for(int i=(a);i<(b);i++)
#define CLR(x,m) memset(x,m,sizeof x);
#define LOCAL freopen("test.txt","r",stdin)
#define UCCU ios::sync_with_stdio(0);
#define XSD(i) cout << fixed << setprecision(i);
#define pii pair<int,int>
#define xx first
#define yy second

using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef double DB;
typedef long double LDB;

const double eps = 1e-8;
//const int inf = 1<<30;
const int INF = 0x3f3f3f3f;
const long long llinf = (long long)300100*1000000000;
const DB PI = acos(-1.0);
const LL mod = 1e9+7;

//-----------------------------------------------------------------------
const int MAXN = 100 + 10;
const int MAXM = 8100 + 10;
struct Edge{
    int to,next,cap,flow,cost;
}edge[MAXM];
int tol,head[MAXN];
int pre[MAXN],dis[MAXN];
bool vis[MAXN];
int N,M,K;
void init(){
    tol = 0;
    memset(head,-1,sizeof head);
}
void addedge(int u,int v,int cap,int cost){
    edge[tol].to = v;
    edge[tol].cap = cap;
    edge[tol].cost = cost;
    edge[tol].flow = 0;
    edge[tol].next = head[u];
    head[u] = tol++;
    edge[tol].to = u;
    edge[tol].cap = 0;
    edge[tol].cost = -cost;
    edge[tol].flow = 0;
    edge[tol].next = head[v];
    head[v] = tol++;
}
bool spfa(int s,int t){
    queue<int> q;
    for(int i=1;i<=N+N;i++){
        dis[i] = INF;
        vis[i] = false;
        pre[i] = -1;
    }
    dis[s] = 0;
    vis[s] = true;
    q.push(s);
    while(!q.empty()){
        int u = q.front();
        q.pop();
        vis[u] = false;
        for(int i=head[u];i!=-1;i=edge[i].next){
            int v = edge[i].to;
            if(edge[i].cap>edge[i].flow && dis[v] > dis[u] + edge[i].cost){
                dis[v] = dis[u] + edge[i].cost;
                pre[v] = i;
                if(!vis[v]){
                    vis[v] = true;
                    q.push(v);
                }
            }
        }
    }
    if(pre[t]==-1) return false;
    if(dis[t]>K) return false;
    return true;
}
int minCostMaxflow(int s,int t,int &cost){
    int flow = 0;
    cost  = 0;
    while(spfa(s,t)){
        int Min = INF;
        for(int i=pre[t];i != -1;i = pre[edge[i^1].to]){
            if(Min > edge[i].cap - edge[i].flow) Min = edge[i].cap - edge[i].flow;
        }
        for(int i=pre[t];i!=-1;i=pre[edge[i^1].to]){
            edge[i].flow+=Min;
            edge[i^1].flow-=Min;
            cost += edge[i].cost * Min;
        }
        flow += Min;
    }
    return flow;
}
int main(){
    while(cin>>N>>M>>K&&N&&M&&K){
        init();
        for(int i=2;i<N;i++) addedge(i,i+N,1,0);
        for(int i=0;i<M;i++){
            int a,b;cin>>a>>b;
            if(a==1||a==N) addedge(a,b,INF,1);
            else addedge(a+N,b,INF,1);
        }
        int cost;
        cout<<minCostMaxflow(1,N,cost)<<endl;
    }
}

至此，我所有的搜索专题，全部完成了，接下来就会做kuangbin专题三了，到时候有空再说。谢谢。

posted @ 2020-10-09 19:41 Bug_Clearlove 阅读(296) 评论(0) 编辑收藏举报

刷新页面返回顶部

Bug_Clearlove

高级搜索题集

Key Task HDU - 1885

Full Tank?POJ - 3635

Continuous Same Game (2)HDU - 2259

Prison Break HDU - 3681

公告