容斥

怒 升 √

CF1228E Another Filling the Grid

题意：

给定一个 \(n\times n\) 的矩阵，可以在矩阵中的任意位置填范围在 \([1,K]\) 之间的数，要求每行每列的最小值都为 \(1\)，求总方案数 \(\operatorname{mod} 1e9+7\) 的结果。

\(n\le 250,K\le 1e9\)

解题思路：

梦开始的地方。

考虑容斥。

答案即为总方案数减去至少一行或一列最小值不为 \(1\) 的方案数。

首先思考这个矩阵只有一行的情况下该怎么容斥（一维）：

\[ans=\sum_{i=1}^{n}(-1)^{i-1} \binom{n}{i}(K-1)^iK^{n-i} \]

即从其中至少 \(i\) 列的最小值不能是 \(1\)，其他的位置随便选的方案数。容易证明通过上式求得的是存在一列最小值不是 \(1\) 的并集（加上选出 \(1\) 列最小值不为 \(1\)的情况，减去重了的选出 \(2\) 列最小值不为 \(1\)的情况...）。

接下来将其推广到二维的形式。

从 \(n\) 行之中选出了 \(i\) 行，从 \(n\) 列之中选出了 \(j\) 列，所选出的位置个数实际上是 \(n\times i+n\times j-i\times j\) （交叉的格子会多算一遍所以要减掉）。若想使选出来的行或列不合法，那么这些位置一定填的是大于 \(1\) 的数，而剩下的 \(n^2-n\times i-n\times j +i\times j\) 个位置可以任意选，因为条件是“至少”。

再类比一维的容斥，我们可以得出下式：

\[ans=\sum_{i=0}^{n}\sum_{j=0}^{n}(-1)^{i+j} \binom{n}{i}\binom{n}{j}(K-1)^{n\times i+n\times j-i\times j}K^{(n-i)(n-j)} \]

（已经把“至少 \(0\) 行 \(0\) 列最小值不为 \(1\) ”的全集放进了式子里）

通过预处理 \(K-1\) 和 \(K\) 的幂可以做到 \(O(n^2)\) 的复杂度。

能不能再给力一点儿？

观察上式，发现我们可以把后面两项拆开，把含 \(j\) 的东西提出来。

\[\sum_{i=0}^{n}\sum_{j=0}^{n}(-1)^{i+j} \binom{n}{i}\binom{n}{j}(K-1)^{n\times i+n\times j-i\times j}K^{n^2-n\times i-n\times j +i\times j } \\ \sum_{i=0}^{n}\sum_{j=0}^{n}(-1)^{i+j} \binom{n}{i}\binom{n}{j}(K-1)^{n\times i}K^{n^2-n\times i} [(K-1)^{n-i} K^{i-n}]^{j}\\ \sum_{i=0}^{n}(-1)^{i} \binom{n}{i}(K-1)^{n\times i}K^{n^2-n\times i}\sum_{j=0}^{n}(-1)^j \binom{n}{j}[(K-1)^{n-i} K^{i-n}]^{j} \]

后面那部分实际上可以用二项式定理化成：

\[\sum_{i=0}^{n}(-1)^{i} \binom{n}{i}(K-1)^{n\times i}K^{n^2-n\times i}[1-(K-1)^{n-i} K^{i-n}]^n \\ \sum_{i=0}^{n}(-1)^{i} \binom{n}{i}[(K-1)^{i}K^{n- i}-(K-1)^{n} ]^n \]

然后这玩意儿就能 \(O(n\log n)\) 做了。

一种理解是在 \(n\) 列中选出 \(i\) 列最小值大于 \(1\) 并减去行合法的情况，由于满足条件之后所有的行是等价的，所以能直接上一行方案的 \(n\) 次幂。

P6076 [JSOI2015]染色问题

题意：

给定一个 \(n\times m\) 的网格，每个格子可以选择染上 \([1,c]\) 范围内的颜色或者不染色。

要求：

1. 每一行至少存在一个格子被染过颜色。

2. 每一列至少存在一个格子被染过颜色。

3. 每种颜色至少被在网格中出现过一次。

求总方案数 \(\operatorname{mod} 1e9+7\) 的结果。

\(n,m,c\le 400\)

解题思路：

如果懂了上一道题的思路，这一道大概很好做（逃

考虑只对颜色进行容斥，所有颜色至少都出现过一次的方案数为：

\[v=\sum_{i=1}^{c}(-1)^{i-1} \binom{c}{i}(c-i+1)^{x} \]

（\(x\) 表示哪些位置可以任意染色或者不染色）

接着考虑如何求出满足条件的行和列。发现在颜色合法的情况下只需要对行和列进行容斥即可。因此至少 \(i\) 行 \(j\) 列没有染色的方案数可表示为：

\[\sum_{i=0}^{n}\sum_{j=0}^{n}(-1)^{i+j} \binom{n}{i}\binom{n}{j}\sum_{k=1}^{c}(-1)^{k-1} \binom{c}{k}(c-k+1)^{(n-i) (n-j)} \]

结合预处理可以做到 \(O(n^3)\) 。

能不能再给力一点儿？

设 \(f_i\) 为最多只用 \(i\) 种颜色满足行列限制的方案数，对颜色进行容斥有：

\[f_c=\sum_{j=1}^{j} (-1)^j\binom{c}{j} f_{j} \]

这要求我们先求出 \(f_i\) 。

依然是先使行满足条件然后选择对列进行容斥，只选 \(i\) 种颜色，至少 \(k\) 列不染色时，每行的方案数为 \((i+1)^{m-j}-1\) （减去行不染色的情况），因此得到下式：

\[f_i=\sum_{k=0}^{m} (-1)^{k}\binom{m}{k} [(i+1)^{m-k}-1]^n \]

复杂度 \(O(n^2 \log n)\) 。

CF997C Sky Full of Stars

题意：

有一个 \(n \times n\)（ \(n \leq 10^6\) ）的正方形网格，用红色，绿色，蓝色三种颜色染色，求有多少种染色方案使得至少一行或一列是同一种颜色。结果对 \(998244353\) 取模。

解题思路：

我的做法可能会有些小麻烦（？

观察到颜色数比较少，我们可以先求出至少一行或一列是红绿蓝其中的某一种颜色的方案数。

考虑容斥，先选定至少 \(i\) 行 \(j\) 列是同一种颜色，这样的位置一共有 \(n\times i+n\times j-i\times j\) 个，其他 \(n^2-n\times i-n\times j +i\times j\) 个位置可以任意选，方案数为：

\[ansone=3^{n^2}-\sum_{i=0}^{n}\sum_{j=0}^{n}(-1)^{i+j} \binom{n}{i}\binom{n}{j} 3^{(n-i)(n-j)} \]

（因为后面的式子容斥出来的实际上是不满足条件的数，所以要用全集 \(3^n\) 减去）

于是我们求出了至少使用一种颜色（以下矩形范围）的方案数，如图所示。

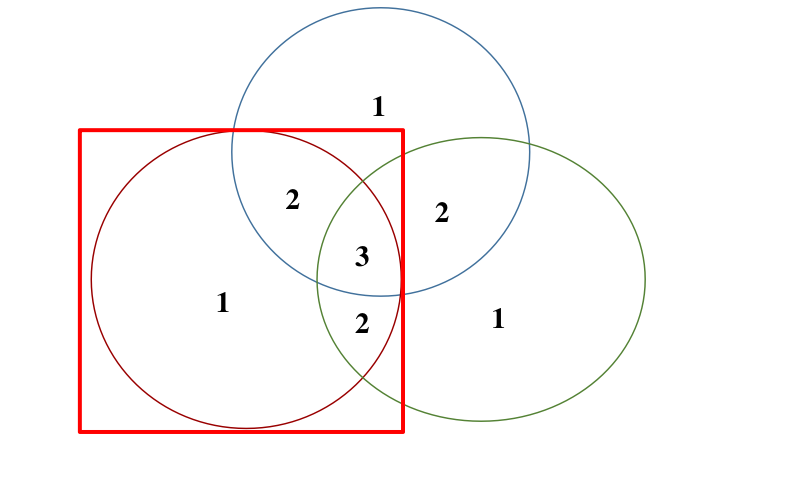
然而直接将 \(ansone \times 3\) 会导致 \(2,3\) 部分出现重复，因此接下来需要分别求出使用两种颜色和使用三种颜色满足要求的方案数，最后容斥出最终结果。

观察到当有行或者列出现同种颜色且这些颜色种类数大于 \(1\) 时，情况一定是只有行符合条件或者只有列符合条件（因为行列交叉处显然不能出现多种颜色）。这启发我们只需要针对行进行容斥，并将方案数乘以 \(2\) 即可。

考虑至少选用了两种颜色的方案：

\[anstwo=[\sum_{i=2}^{n} (-1)^i \binom{n}{i}(2^i-2)3^{(n-i)i}]\times 2 \]

（ \(2^i-2\) 的含义是这些行可以选择两种颜色，但不能都选择同一种颜色的方案数）

至少选用了三种颜色的方案：

\[ansthr=[\sum_{i=3}^{n} (-1)^{i-1} \binom{n}{i}(3^i-3(2^i-2)+3)3^{(n-i) i})]\times 2 \]

（ \(3^i-3(2^i-2)+3\) 的含义是这些行可以选择三种颜色，但不能都选择两种相同颜色或者一种相同颜色的方案数）

至此我们求出来了所有的部分，因此最终的答案应该为：

\[ans=ansone\times 3-anstwo \times 3+ansthr \]

结合预处理可以做到 \(O(n^2)\) 。

然后悲哀地发现数据范围是 \(10^6\) 的。

所以就大力卡常思考怎么样优化复杂度。

回过头来看求 \(ansone\) 的第一个式子：

\[3^{n^2}-\sum_{i=0}^{n}\sum_{j=0}^{n}(-1)^{i+j} \binom{n}{i}\binom{n}{j}3^{(n-i)(n-j)} \]

观察后面那一部分，把含 \(j\) 的项都分离出来：

\[\sum_{i=0}^{n}\sum_{j=0}^{n}(-1)^{i+j} \binom{n}{i}\binom{n}{j}3^{(n-i)(n-j)} \\ \sum_{i=0}^{n}\sum_{j=0}^{n}(-1)^{i}(-1)^{j} \binom{n}{i}\binom{n}{j} 3^{(n-i)n+(i-n)j} \\ \sum_{i=0}^{n}(-1)^{i} \binom{n}{i}3^{(n-i)n} \sum_{j=0}^{n} (-1)^{j} \binom{n}{j} 3^{(i-n)j} \]

发现后面可以用二项式定理化成：

\[\sum_{i=0}^{n}(-1)^{i} \binom{n}{i}3^{(n-i)n}(1-3^{i-n})^n \]

然后这题就可以 \(O(n\log n)\) 做了。

代码：

变量有些丑，而且懒得预处理了（逃

#include <cstdio>
#include <algorithm>
#define Reg register
#define int long long
using namespace std;
const int maxn=1000010,mod=998244353;
int n,ans,ansone,anstwo,ansthr;
int ark[maxn],arknv[maxn];
inline int read(){
    int s=0,w=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        s=(s<<1)+(s<<3)+(ch^48);
        ch=getchar();
    }
    return s*w;
}
inline int qpow(int A,int B){
    int Ans=1;
    while(B){
        if(B&1) Ans=Ans*A%mod;
        A=A*A%mod;
        B>>=1;
    }
    return Ans;
}
inline void pre(){
    int p=max(n,3ll);
    ark[0]=arknv[0]=1;
    for(Reg int i=1;i<=p;++i) ark[i]=ark[i-1]*i%mod;
    arknv[p]=qpow(ark[p],mod-2);
    for(Reg int i=p-1;i;--i) arknv[i]=arknv[i+1]*(i+1)%mod;
}
inline int C(int p,int q){
    if(p<q) return 0;
    return ark[p]*arknv[p-q]%mod*arknv[q]%mod;
}
signed main(){
    n=read(),pre();
    for(Reg int i=0;i<=n;++i){
        int v=qpow(3,n-i)%mod,p=(i&1)?mod-1:1;
        v=qpow(v,mod-2)%mod;
        v=qpow(1-v+mod,n)%mod;
        ansone=(ansone+p%mod*C(n,i)%mod*qpow(3,n*(n-i))%mod*v%mod);
    }
    ansone=((qpow(3,n*n)-ansone+mod)%mod+mod)%mod;
    for(Reg int i=2;i<=n;++i){
        int p=(i&1)?mod-1:1;
        anstwo=(anstwo+p*C(n,i)%mod*(qpow(2,i)-2+mod)%mod*qpow(3,(n-i)*n)%mod)%mod;
    }
    anstwo=anstwo*2%mod;
    for(Reg int i=3;i<=n;++i){
        int p=(i&1)?1:mod-1;
        ansthr=(ansthr+p*C(n,i)%mod*((qpow(3,i)-3*(qpow(2,i)-2)%mod+mod-3)%mod+mod)%mod*qpow(3,(n-i)*n)%mod)%mod;
    }
    ansthr=ansthr*2%mod;
    ans=(((ansone*3%mod-anstwo*3%mod+mod)%mod+mod)%mod+ansthr)%mod;
    printf("%lld\n",ans);
    return 0;
}