[软件工程]——代码练习之螺旋数据分类

PyTorch基础

在学习pytorch基础语法时，直接运行以下段时报错。

import torch
m = torch.Tensor([[2,5,3,7], [4,2,1,9]])
v = torch.arange(1, 5)
print(m @ v) # @ 点积运算


# RuntimeError: expected scalar type Float but found Long

这是因为tensor的数据类型不匹配造成的问题。

# torch.Tensor()是Python类，是默认张量类型torch.FloatTensor()的别名，生成单精度浮点类型的张量。
x = torch.Tensor([1, 2 ,3, 4])

#torch.tensor()仅仅是Python的函数，根据原始数据类型生成相应的torch.LongTensor
x = torch.tensor([1, 2, 3, 4])

因此我们在使用时，需要注意类型统一，可以使用dtype进行设置

v = torch.arange(1, 5, dtype = torch.float)
print(m @ v)

螺旋数据分类demo

初始化一些参数

import random
import torch
from torch import nn, optim
import math
from IPython import display
from plot_lib import plot_data, plot_model, set_default

# 在cpu上运行torch 
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print('device: ', device)

# 初始化随机数种子。神经网络的参数都是随机初始化的，
# 不同的初始化参数往往会导致不同的结果，当得到比较好的结果时我们通常希望这个结果是可以复现的，
# 因此，在pytorch中，通过设置随机数种子也可以达到这个目的
seed = 12345
random.seed(seed)
torch.manual_seed(seed)

N = 1000  # 每类样本的数量
D = 2  # 每个样本的特征维度
C = 3  # 样本的类别
H = 100  # 神经网络里隐层单元的数量

 构造样本

X = torch.zeros(N * C, D).to(device)
Y = torch.zeros(N * C, dtype=torch.long).to(device)
for c in range(C):
    index = 0
    t = torch.linspace(0, 1, N) # 在[0，1]间均匀的取10000个数，赋给t
    # 下面的代码不用理解太多，总之是根据公式计算出三类样本（可以构成螺旋形）
    # torch.randn(N) 是得到 N 个均值为0，方差为 1 的一组随机数，注意要和 rand 区分开
    inner_var = torch.linspace( (2*math.pi/C)*c, (2*math.pi/C)*(2+c), N) + torch.randn(N) * 0.2
    
    # 每个样本的(x,y)坐标都保存在 X 里
    # Y 里存储的是样本的类别，分别为 [0, 1, 2]
    for ix in range(N * c, N * (c + 1)):
        X[ix] = t[index] * torch.FloatTensor((math.sin(inner_var[index]), math.cos(inner_var[index])))
        Y[ix] = c
        index += 1

print("Shapes:")
print("X:", X.size())
print("Y:", Y.size())

其中，

X可以理解为特征矩阵，共有3000个样本，每个样本的特征维度是2维，因此X是一个N*C行，D列的矩阵。

Y可以理解为样本标签，所以是一个N*C行的一维矩阵

最后得出的样本是这个样子的：

 

 构建线性模型分类

learning_rate = 1e-3
lambda_l2 = 1e-5

# nn 包用来创建线性模型
# 每一个线性模型都包含 weight 和 bias
model = nn.Sequential(
    nn.Linear(D, H), # 2*100
    nn.Linear(H, C)  # 100*3
)
model.to(device)

# nn 包含多种不同的损失函数，这里使用的是交叉熵（cross entropy loss）损失函数
criterion = torch.nn.CrossEntropyLoss()

# 这里使用 optim 包进行随机梯度下降(stochastic gradient descent)优化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)

# 开始训练
for t in range(1000):
    # 把数据输入模型，得到预测结果
    y_pred = model(X)
    # 计算损失和准确率
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = (Y == predicted).sum().float() / len(Y)
    print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
    display.clear_output(wait=True)

    # 反向传播前把梯度置 0 
    optimizer.zero_grad()
    # 反向传播优化 
    loss.backward()
    # 更新全部参数
    optimizer.step()

其中，

nn.Sequential是一个有序容器，神经网络模块将按照传入构造器的顺序依次被添加到计算图中执行。

nn.Linear用于设置神经网络的全连接层， 在二维图像处理中，其输入输出一般是二维张量。

这里直接使用了两个线性模型，第一个是2*100（2个特征维度到100个隐层单元），第二个是100*3（100个隐层单元到最终的3个类别）

我们打印出model来，也可以看到这样的结构。

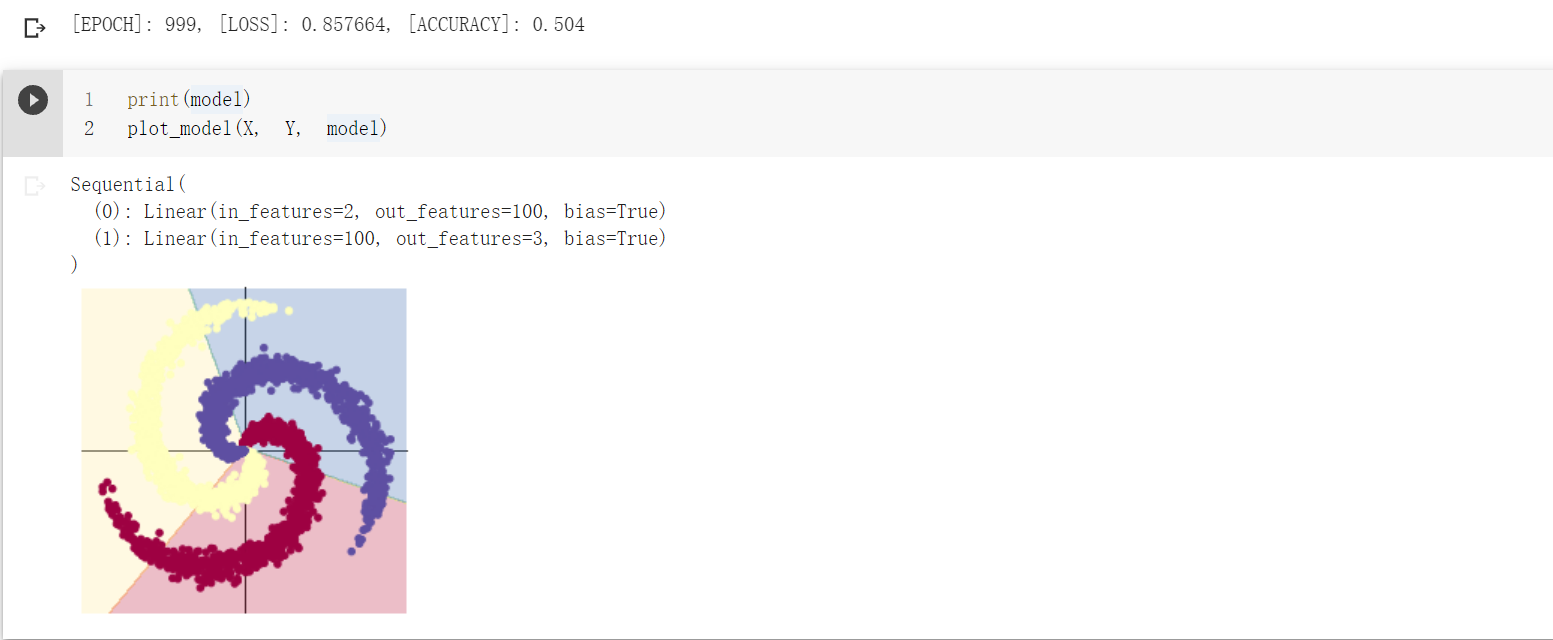
print(model)
'''
Sequential(
  (0): Linear(in_features=2, out_features=100, bias=True)
  (1): Linear(in_features=100, out_features=3, bias=True)
)
'''

最终，线性模型的分类效果如下，可以看到分类的结果（分割界限）是线性的。

其正确率只有50%左右，效果较差。

 构建两层神经网络分类

我们在原先的线性模型中进行一些改动，主要是在model中加入一个激活函数ReLU，使其变成一个两层的神经网络

learning_rate = 1e-3
lambda_l2 = 1e-5

# 这里可以看到，和上面模型不同的是，在两层之间加入了一个 ReLU 激活函数
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),      # 加入了激活函数ReLU
    nn.Linear(H, C)
)
model.to(device)

# 下面的代码和之前是完全一样的，这里不过多叙述
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2

# 训练模型，和之前的代码是完全一样的
for t in range(1000):
    y_pred = model(X)
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = ((Y == predicted).sum().float() / len(Y))
    print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
    display.clear_output(wait=True)
    
    # zero the gradients before running the backward pass.
    optimizer.zero_grad()
    # Backward pass to compute the gradient
    loss.backward()
    # Update params
    optimizer.step()

因为线性模型的表达力不够，所以我们使用了激活函数，用来加入非线性因素。

ReLU函数很简单，表达形式如下：

f(x) = max(0, max)

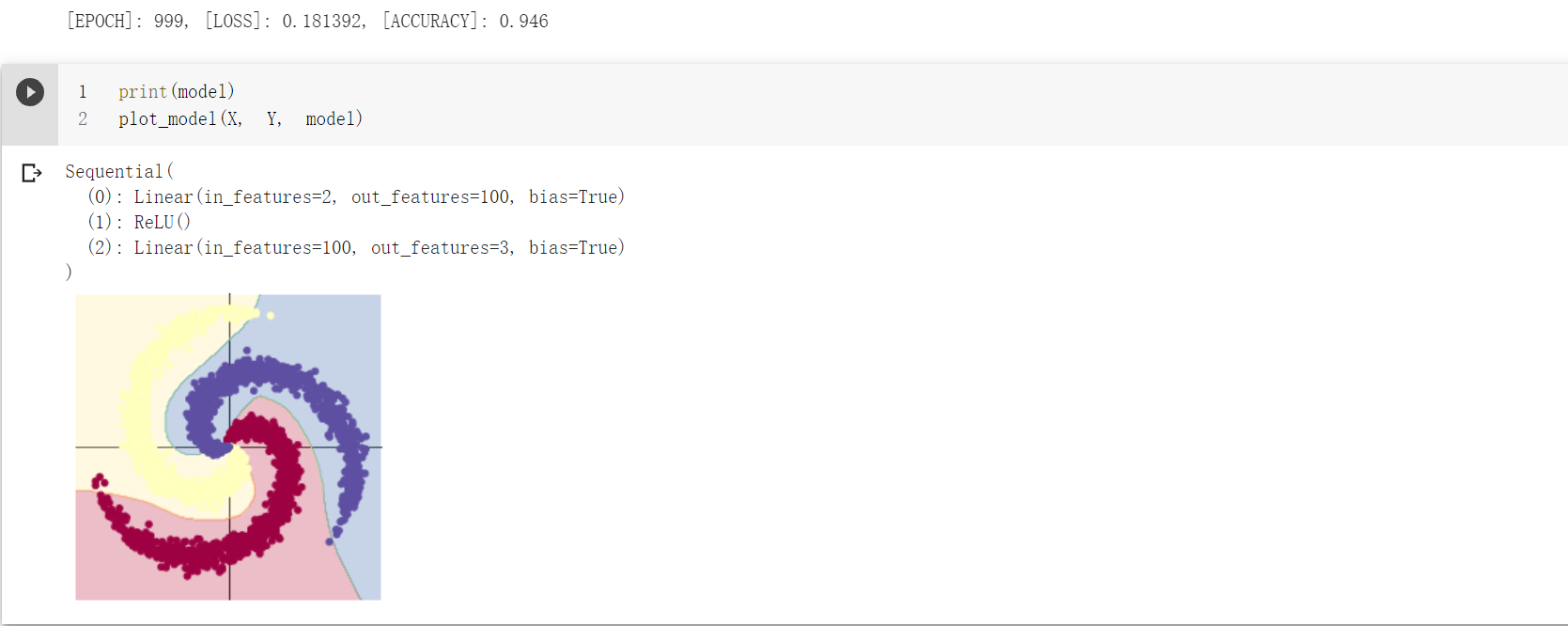
加入ReLU函数的两层神经网络最终的分类效果如下：

其准确率已经达到了95%左右，效果非常明显。

 我们知道增加神经网络的节点数和层数可以使其获得更好的逼近效果，因此我们可以尝试修改一下model，使其多一层。

learning_rate = 1e-3
lambda_l2 = 1e-5


model = nn.Sequential(  
    nn.Linear(2, 100),                #2*100 -> 100*50 -> 50*3
    nn.ReLU(),     
    nn.Linear(100, 50),# 增加一层
    nn.ReLU(),         # 增加一个激活函数
    nn.Linear(50, 3)
)
model.to(device)
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)



for t in range(1000):
  y_pred = model(X)
  loss = criterion(y_pred, Y)
  score, predicted = torch.max(y_pred, 1)
  acc = ((Y == predicted).sum().float() / len(Y))
  print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
  display.clear_output(wait=True)
    
  optimizer.zero_grad()
  loss.backward()
  optimizer.step()

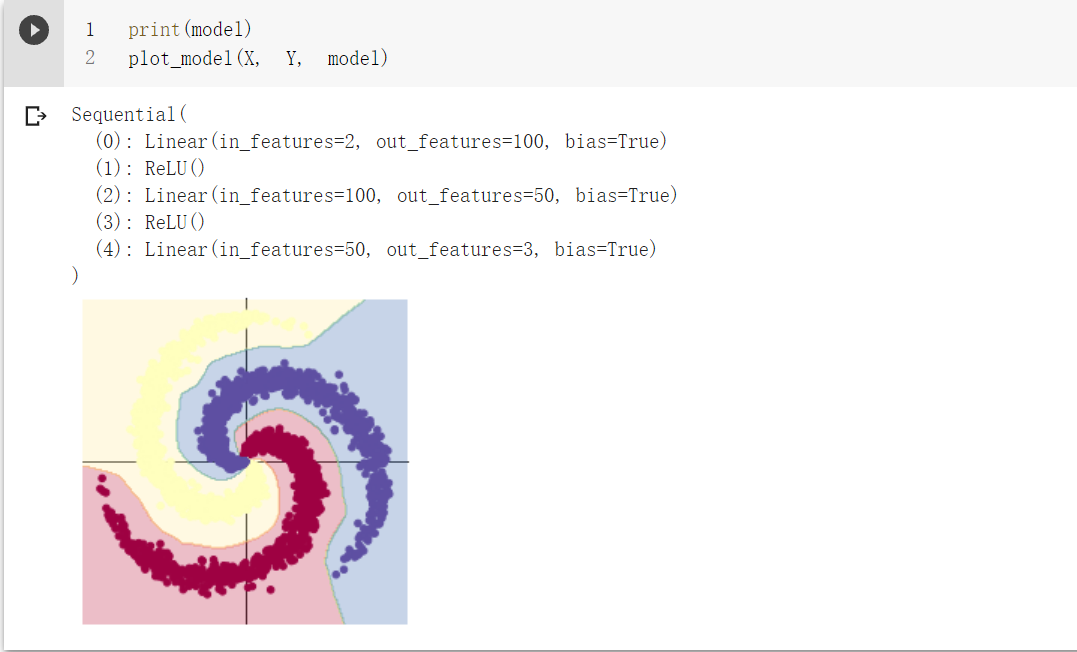
运行后，发现结果的准确率达到了0.999，效果更明显。