P11244 解题报告
题目传送门
题目大意已经很清楚，不再赘述。
思路：
将所有序列的状态分为 \(3\) 个阶段。
先给出一个定义，序列的跨度：
定义一个序列 \(a\)，设其中的最大值为 \(r\)，最小值为 \(l\)，那么它的跨度为 \([l, r]\)。
第一阶段：
首先注意到 \(m\le 20\)，而且每次操作 \(1\) 都会将两个序列排好序，所以不难发现一些操作后所有的序列都有序了，所以可以记录一下哪些序列是有序的，若当前操作的序列无序再用 \(\operatorname{sort}\) 把它变成有序的。每个序列都最多 \(\operatorname{sort}\) 一遍，总时间复杂度不会超过 \(O(mn\log n)\)。
第二阶段：
当所有序列都有序后再进行操作 \(1\)，还可能会出现值域相交的情况（这里的相交定义为跨度代表的区间除掉端点后有交集）。比如 \(\{1, 3, 4, 5\}\) 和 \(\{2, 4, 5, 6\}\)。这时候由于序列已经有序了，所以可以直接进行归并，最多进行 \(m^2\) 次归并就能使得所有序列两两值域都不相交，总时间复杂度不会超过 \(O(m^2n)\)（至于为什么将在下文讨论）。
第三阶段：
这时候操作 \(1\) 的本质已经变为了交换两个序列，但我们不用真的交换，从一开始就建立一个 \(id\) 数组记录每一个序号究竟对应哪一个序列，对于每个询问直接交换对应的 \(id\) 值即可，单次询问时间复杂度 \(O(1)\)。
那么为什么第二阶段的归并次数不会超过 \(m^2\) 呢？事实上，不会超过 \(\frac{m(m - 1)}{2}\)。
这里我用了数学归纳法来证明。
命题：有 \(m\) 个序列且都有序的情况下，第二阶段的归并次数不会超过 \(\frac{m(m - 1)}{2}\)。
当 \(m = 1\) 时，归并次数为 \(0\)，显然不会超过 \(\frac{m(m - 1)}{2}\)。
当 \(m = k\) 时假设命题成立，即“有 \(k\) 个序列且都有序的情况下，第二阶段的归并次数不会超过 \(\frac{k(k - 1)}{2}\)”。
那么当 \(m = k + 1\) 时，相当于在原来的基础上多加了一个序列，那么由于前 \(k\) 个序列已经两两互不相交，那么只需考虑有关第 \(k + 1\) 个序列的操作。
引理1：
设两个序列为 \(x, y\) 且 \(x,y\) 的跨度不是包含关系，\(y\) 的跨度的右端点大于等于 \(x\) 的跨度右端点，则对于操作 \(\texttt{1 x y}\) 进行了有效归并操作后，设原来的跨度分别为 \(S_1,S_2\)，新得到的跨度分别为 \(S_1',S_2'\)，则有\[S_1'\subseteq S_1,S_2'\subseteq S_2 \]证明：
设 \(x\) 中的最大值为 \(mx_x\)，最小值是 \(mn_x\)，\(y\) 中的最大值为 \(mx_y\)，最小值是 \(mn_y\)，那么 \(x\) 的跨度为 \(S_1 = [mn_x, mx_x]\)，\(y\) 的跨度为 \(S_2 = [mn_y, mx_y]\)。
因为只有当 \(mx_x > mn_y\) 时才归并，且归并必定将足够多的等于 \(mx_x\) 的项移到 \(y\) 中，也必定会将足够多的等于 \(mn_y\) 的项移到 \(x\) 中。
设新得到的 \(x,y\) 的跨度分别为 \(S_1' = [l_x, r_x],S_2' = [l_y, r_y]\)，那么必然有 \(r_x \le mx_x,l_y \ge mn_y\)，而 \(l_x = mn_x,r_y = mx_y\) 这两个不会变，故有 \(S_1'\subseteq S_1,S_2'\subseteq S_2\)。
证明完毕。
这说明：当所有操作的两个序列跨度不相互包含时，设势能函数 \(F(k + 1)\) 表示与第 \(k + 1\) 个序列相交的序列数，显然这个数不会大于 \(k\)，又因为只有相交我们才归并，根据引理 \(1\) 可知，每次归并只会使得这个数 \(-1\) 而不会使它增加，所以最多 \(k\) 次操作就能使它变为 \(0\)，即此时第 \(k + 1\) 个序列不与其它 \(k\) 个序列相交。
并且根据引理 \(1\)，其他的 \(k\) 个序列原本就各不相交，在操作后肯定也各不相交，所以在此种情况下，第二阶段的归并次数不会超过 \(\frac{k(k - 1)}{2} + k = \frac{k(k + 1)}{2}\)。
但是还有一种可能：当两个序列的跨度相互包含的情况呢？
显然上述引理就不满足了，比如归并 \(\{1, 1, 2, 3, 4\}\) 和 \(\{2, 2, 2, 2, 2\}\)，第二个序列的跨度显然会扩大。
表面上看起来第二个序列变为了 \(\{2, 2, 3, 3, 4\}\) 可能和之前的 \(k\) 个序列相交从而产生新的势能但是实际上产生的势能不会大于降低的势能。
先考虑以下这种情况：
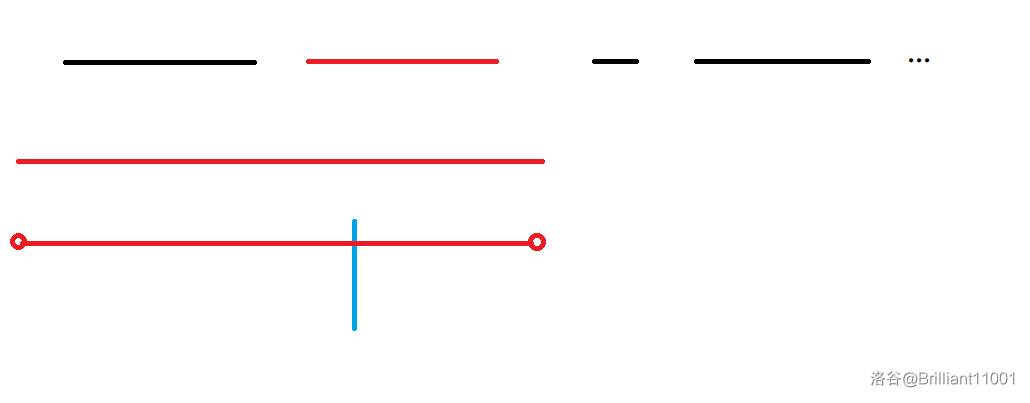
第一行表示的是已经互不相交的 \(k\) 个序列，第二行是现在考虑的第 \(k + 1\) 个，只从相交的序列中选择一个来操作，现在不妨操作这两个红色的序列（其他的都是同理），上记为 \(A\)，下记为 \(B\)，操作后为 \(A',B'\)。
左红圈表示 \(A'\) 的左端点，右红圈表示 \(B'\) 的右端点，蓝色线 \(k\) 表示操作完后 \(A, B\) 的跨度右端点和左端点（有可能不重合，但最多只会相差 \(1\)），由于将小的元素放在上面或下面都是对称的，所以不妨放上面。
那么很轻松就能得出蓝色线一定是在 \(A\) 的右端点左边的，即 \(k\le r_A'\)，设原来 \(A,B\) 产生的势能 \(F(A) = 0, F(B) = cnt\)。
当蓝线往左移动时，\(B\) 的势能每增加 \(1\)，\(A\) 的势能就会减小 \(1\)，且本次操作消除了 \(A, B\) 之间的势能 \(1\)，那么操作后假设 \(F(A) = \lambda\)，则 \(F(B) = cnt - \lambda - 1\)，总势能永远都是 \(-1\) 的。
\(F(k + 1)\le k\) 所以最多操作 \(k\) 次就能使得势能减为 \(0\)，所以在此种情况下，第二阶段的归并次数也不会超过 \(\frac{k(k + 1)}{2}\)。
证明完毕。
综上所述：总的时间复杂度不会超过 \(O(nm\log n + m^2n + q)\)，可以通过此题。
非常感谢你还能看到这里，本人实力有限，这种证明方法感觉太过繁琐，不如官方题解的证明。
（先猜后证）
\(\texttt{Code:}\)
#include <queue>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2000010;
int n, m, q;
int a[21][N];
bool st[N];
int tmp[N << 1];
int id[21];
int main() {
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
scanf("%d", &a[i][j]);
for(int i = 1; i <= m; i++) id[i] = i;
int op, x, y;
while(q--) {
scanf("%d%d%d", &op, &x, &y);
if(op == 1) {
int xx = x, yy = y;
x = id[x], y = id[y];
if(st[x] && st[y]) {
if(a[x][n] > a[y][1]) {
if(a[x][1] >= a[y][n])
swap(id[xx], id[yy]);
else {
int pos1 = lower_bound(a[x] + 1, a[x] + n + 1, a[y][1]) - a[x];
int pos2 = lower_bound(a[y] + 1, a[y] + n + 1, a[x][n]) - a[y];
if(a[x][pos1] == a[y][1]) pos1++;
if(a[y][pos2] == a[x][n]) pos2--;
if(pos2 == n + 1) pos2--;
int p1 = pos1, p2 = 1, top = 0;
while(p1 <= n && p2 <= pos2) {
if(a[x][p1] < a[y][p2]) tmp[++top] = a[x][p1++];
else tmp[++top] = a[y][p2++];
}
while(p1 <= n) tmp[++top] = a[x][p1++];
while(p2 <= pos2) tmp[++top] = a[y][p2++];
top = 1;
for(int i = pos1; i <= n; i++)
a[x][i] = tmp[top++];
for(int i = 1; i <= pos2; i++)
a[y][i] = tmp[top++];
}
}
}
else {
if(!st[x]) sort(a[x] + 1, a[x] + n + 1);
if(!st[y]) sort(a[y] + 1, a[y] + n + 1);
st[x] = st[y] = true;
int pos1 = lower_bound(a[x] + 1, a[x] + n + 1, a[y][1]) - a[x];
int pos2 = lower_bound(a[y] + 1, a[y] + n + 1, a[x][n]) - a[y];
if(a[x][pos1] == a[y][1]) pos1++;
if(a[y][pos2] == a[x][n]) pos2--;
if(pos2 == n + 1) pos2--;
int p1 = pos1, p2 = 1, top = 0;
while(p1 <= n && p2 <= pos2) {
if(a[x][p1] < a[y][p2]) tmp[++top] = a[x][p1++];
else tmp[++top] = a[y][p2++];
}
while(p1 <= n) tmp[++top] = a[x][p1++];
while(p2 <= pos2) tmp[++top] = a[y][p2++];
top = 1;
for(int i = pos1; i <= n; i++)
a[x][i] = tmp[top++];
for(int i = 1; i <= pos2; i++)
a[y][i] = tmp[top++];
}
}
else printf("%d\n", a[id[x]][y]);
}
return 0;
}
其实也可以用 vector 直接 \(O(1)\) 交换，就不用写 \(id\) 数组了。（只是需要做一些下标上的转换）
这一场怎么这么奇怪？
