P3193 [HNOI2008] GT考试 解题报告

合集 - 数学(8)

1.数学知识（一）2023-12-26

2.P3193 [HNOI2008] GT考试 解题报告2024-09-02

3.P7976 解题报告2024-09-114.P10315 解题报告2024-09-115.P10499 解题报告2024-09-116.P11130 解题报告2024-09-297.CF755D 数学规律法 解题报告2024-11-278.数学知识（二）01-22

收起

题目传送门

题目大意：

给定一个长度为 $m$ 且只含 $0\sim 9$ 的字符串 $s$，求出所有长度为 $n$ 的，只含 $0\sim 9$ 且不含 $s$ 字符串的数量，结果对 $mod$ 取模。

数据范围：$n\le {10}^9,m\le 20,k\le 1000$。

思路：

不难发现和 这道题 很像，只是 $n$ 的数据范围被扩大到了 ${10}^9$，$m$ 的范围被缩小到了 $20$。

朴素 dp 思路在 状态机模型 dp 中写了，这里只讲优化。

朴素做法的时间复杂度为 $O(nm)$，由于这道题的 $n$ 很大，所以 TLE 无疑了。

观察一下状态转移方程：

$$f(i+1,\delta (\pi (j),ch))\leftarrow f(i,j)$$

对于每个 $j$，它有 $10$ 种状态，分别是字符 $0\sim 9$，而若 $j$ 和将要填的字符 $ch$ 一定，那么 $\delta (\pi (j),ch)$ 显然也一定，即转移到的地方也相同，而这种转移对于每一个 $i$ 都要做一次，所以应该优化这个过程。

把状态转移方程展开，以 $f(i+1,0\sim m-1)$ 这一层为例：

$$\{\begin{array}{ccc}f(i+1,0)=a_{0,0}\times f(i,0)+a_{1,0}\times f(i,1)+\cdots +a_{m-1,0}\times f(i,m-1)& & \\ f(i+1,1)=a_{0,1}\times f(i,0)+a_{1,1}\times f(i,1)+\cdots +a_{m-1,1}\times f(i,m-1)& & \\ ⋮& & \\ f(i+1,m-1)=a_{0,m-1}\times f(i,0)+a_{1,m-1}\times f(i,1)+\cdots +a_{m-1,m-1}\times f(i,m-1)& & \end{array}$$

这不就是矩阵乘法的形式吗？

根据上面的分析，我们构造的矩阵 $A$ 与 $i$ 无关，所以设 $F(i)=\left[\begin{array}{cccc}f(i,0)& f(i,1)& \cdots & f(i,m-1)\end{array}\right]$，那么 $F(i+1)=F(i)\times A$，不难推出 $F(n)=F(0)\times A^n$，然后就可以用矩阵快速幂算了。

现在的问题变成了如何构造矩阵 $A$。

根据状态转移方程，若 $f(i,j)\to f(i+1,p)$，那么说明要得到 $f(i+1,p)$ 要加上 $f(i,j)$，即 $A$ 矩阵中的第 $j$ 行 $p$ 列要加上 $1$。

为什么呢，看这张图就明白了：

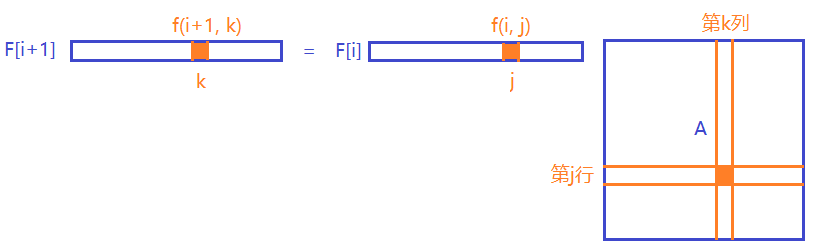
其实图是我偷的（

那么矩阵 $A$ 就构造好了,这道题也做完了。

流程：

先预处理 KMP 的 $ne$ 数组，然后预处理出 $A$ 矩阵，最后直接矩阵快速幂输出答案即可。

时间复杂度：$O(m^3\cdot \log n)$。

$\mathtt{\text{Code:}}$

#include <cstring>
#include <iostream>

using namespace std;

const int N = 25;

int n, m, mod;
char s[N];
int ne[N];

struct Matrix {
    int mar[N][N];
    Matrix() {memset(mar, 0, sizeof mar);}
    void init() {
        memset(mar, 0, sizeof mar);
        for(int i = 0; i < m; i++)
            mar[i][i] = 1;
    }
    Matrix operator *(const Matrix &o) const {
        Matrix res;
        for(int i = 0; i < m; i++)
            for(int j = 0; j < m; j++)
                for(int k = 0 ; k < m; k++)
                    res.mar[i][j] = (res.mar[i][j] + mar[i][k] * o.mar[k][j]) % mod;
        return res;
    }
}A;

int qpow(int k) {
    Matrix res;
    res.mar[0][0] = 1;
    while(k) {
        if(k & 1) res = res * A;
        A = A * A;
        k >>= 1;
    }
    int ans = 0;
    for(int i = 0; i < m; i++)
        ans = (ans + res.mar[0][i]) % mod;
    return ans;
}

int main() {
    scanf("%d%d%d%s", &n, &m, &mod, s + 1);
    for(int i = 2, j = 0; i <= m; i++) {
        while(j && s[j + 1] != s[i]) j = ne[j];
        if(s[j + 1] == s[i]) j++;
        ne[i] = j;
    }
    for(int j = 0; j < m; j++)
        for(int k = '0'; k <= '9'; k++) {
            int p = j;
            while(p && s[p + 1] != k) p = ne[p];
            if(s[p + 1] == k) p++;
            if(p < m) A.mar[j][p]++;
        }
    printf("%d\n", qpow(n));
    return 0;
}