P9847 [ICPC2021 Nanjing R] Crystalfly 题解

题目传送门

甘雨可爱捏

题目大意：

给定一棵有 \(n\) 个节点的树，第 \(i\) 个节点上有 \(a_i\) 只晶蝶，现在从 \(1\) 号点开始走，每走到一个点，获得该点的晶蝶但会惊动相邻点的晶蝶，第 \(i\) 个节点上的晶蝶被惊动后会在 \(t_i\) 后飞走，求问能获得最大晶蝶数量。

数据范围：\(n\le 10^5, 1\le a_i\le 10^9, 1\le t_i\le 3\)。

思路：

很明显是树形 dp。

从条件 \(1\le t_i\le 3\) 入手，这个条件非常重要，因为它意味着晶蝶被惊动后很快就会飞走。

有多快？假如当前走到一个节点 \(i\)，然后立马返回了，那么 \(i\) 的子节点一定全飞走了，就算有的子节点 \(v\) 的 \(t_v = 3\) 还能拿到，但这一定不是最优解（能一步拿到为什么要折返走三步？）。

所以可以分析出几种行走方式：

1. 走到节点 \(i\)，然后走到它的某个子节点处，其他子节点全部飞走；
2. 走到节点 \(i\)，然后走到它的某个子节点 \(v_1\) 处，立即返回，走到另一个 \(t = 3\) 的子节点 \(v_2\) 处，其余子节点全部飞走，\(v_1\) 的子节点也全部飞走。

根据以上分析，我们可以设计出两种状态：

设 \(f(i, 0)\) 表示当前走到点 \(i\)，\(i\) 的蝴蝶已经飞走但子节点还在，我们在以 \(i\) 为根的子树中继续抓蝴蝶最多能抓住几只蝴蝶。

\(f(i, 1)\) 表示当前走到点 \(i\)，然后立马折返回去，即拿到 \(i\) 的蝴蝶，但子节点全部飞走，这种情况下最多能抓住几只蝴蝶。

发现 \(1\) 的状态是可以由 \(0\) 的状态转移到的：

\[f(i, 1) = a_i + \sum\limits_{j\in \text{subtree(i)},j\ne i}f(j, 0) \]

含义就是：第 \(i\) 个点的蝴蝶能抓到，但各个子树的根上的蝴蝶都飞走了。

接下来就只用考虑 \(f(i, 0)\) 怎么计算了。

考虑上面描述的两种行走方式：

设点 \(i\) 的所有子节点 \(j\) 的 \(f(j, 0)\) 之和为 \(sum\)，即：

\[sum = \sum\limits_{j\in \text{subtree(i)},j\ne i}f(j, 0) \]

对于方式 \(1\)，如图所示：

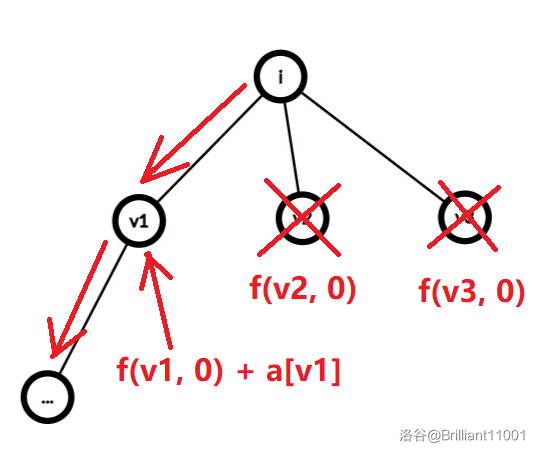
我们要加上所有子节点 \(j\) 的 \(f(j, 0)\)，然后加上走向的那么子节点的蝴蝶数。

状态转移方程为：

\[f(i, 0) = sum + \max\limits_{j\in \text{subtree(i)},j\ne i}a_j \]

对于方式 \(2\)，如图所示：

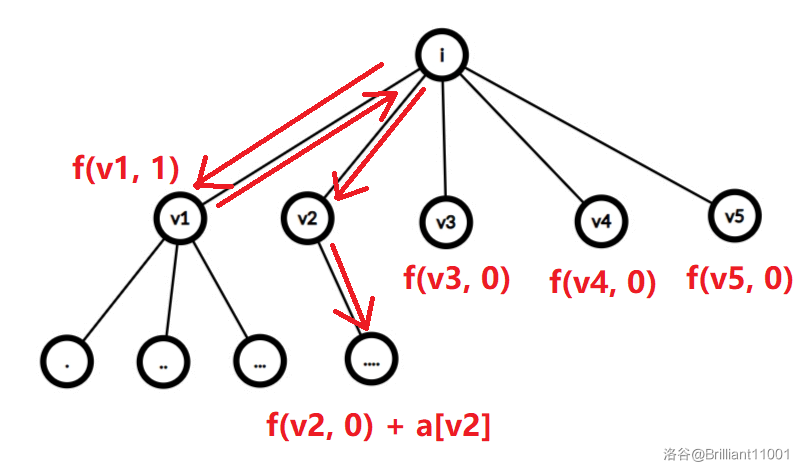
我们要选出两棵子树来走，其他都是 \(f(j, 0)\)。

状态转移方程为：

\[f(i, 0) = sum + \max\limits_{j\in \text{subtree(i)},j\ne i}\{f(j, 1) - f(j, 0)\} + \max\limits_{k\in \text{subtree(i)},k\ne i,k\ne j,t_k = 3}\{a_k\} \]

只考虑 \(t = 3\) 的 \(k\)，不然来不及抓该点的蝴蝶。

朴素思考，要枚举 \(j,k\) 分别求最大值，时间复杂度为 \(O(n^2)\)，TLE。

其实本质上就是求除去一个子结点 \(j\)，剩下的子节点的最大值，因为 \(j\) 必须要枚举，所以就优化找 \(k\) 的过程即可。

可以预处理出子节点中蝴蝶数量的最大值、次大值以及它们分别是哪个子节点。这样的话，在枚举 \(j\) 时若 \(j\) 为最大值所在的那个子节点，就选次大值；否则选最大值，优化掉一层循环。

最后答案即为 \(f(1, 0) + a_1\)。

综上所述，两种行走方式的转移都是 \(O(n)\) 的，所以整个做法的时间复杂度为 \(O(n)\)。

\(\texttt{Code:}\)

#include <vector>
#include <iostream>

using namespace std;

const int N = 100010;
typedef long long ll;
typedef pair<ll, int> PLI;
const ll inf = 0x3f3f3f3f3f3f3f3f;
int T, n;
vector<int> e[N];
int a[N], t[N];
ll f[N][2];

void dfs(int u, int fa) {
    ll sum = 0;
    int maxx = 0;
    for(auto v : e[u]) if(v != fa) {
        dfs(v, u);
        sum += f[v][0];
        maxx = max(maxx, a[v]);
    }
    f[u][0] = sum + maxx;
    //以上是走法一
    PLI maxx1 = {-inf, 0}, maxx2 ={-inf, 0};
    for(auto v : e[u]) if(v != fa && t[v] == 3) {
        PLI now = {a[v], v};
        if(maxx2 < now) maxx2 = now;
        if(maxx1 < maxx2) swap(maxx1, maxx2);
    }
    //以上是预处理最大值和次大值
    for(auto v : e[u]) if(v != fa) {
        ll tmp = sum + f[v][1] - f[v][0];
        if(v == maxx1.second) tmp += maxx2.first;
        else tmp += maxx1.first;
        f[u][0] = max(f[u][0], tmp); 
    }
    //以上是走法二
    f[u][1] = sum + a[u];
}

void solve() {
    for(int i = 1; i <= n; i++) e[i].clear();
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    for(int i = 1; i <= n; i++) scanf("%d", &t[i]);
    for(int i = 1, a, b; i < n; i++) {
        scanf("%d%d", &a, &b);
        e[a].push_back(b);
        e[b].push_back(a);
    }
    dfs(1, -1);
    printf("%lld\n", f[1][0] + a[1]);
}

int main() {
    scanf("%d", &T);
    while(T--) {
        solve();
    }
    return 0;
}