P2163 [SHOI2007] 园丁的烦恼 题解

题目传送门

题目大意：

在一个平面直角坐标系上，给定 \(n\) 个点的坐标 \((x,y)\)，\(m\) 次询问，每次询问一个矩形范围内的点的数量，此矩形用 \(\{a, b, c, d\}\) 来描述，其中 \((a, b)\) 为左下角，\((c, d)\) 为右上角。

思路：

不难将题目转化为：给定一个长度为 \(n\) 的序列，序列中的每个元素都有两个属性 \(x,y\)，每次询问求 \(x\in [a, c]\) 且 \(y\in [b, d]\) 的元素个数。

和 这道题 差不多的思路，都用类似前缀和的思想，但这道题是二维前缀和。

对于一个询问，我们要处理的其实是这样一个图形：

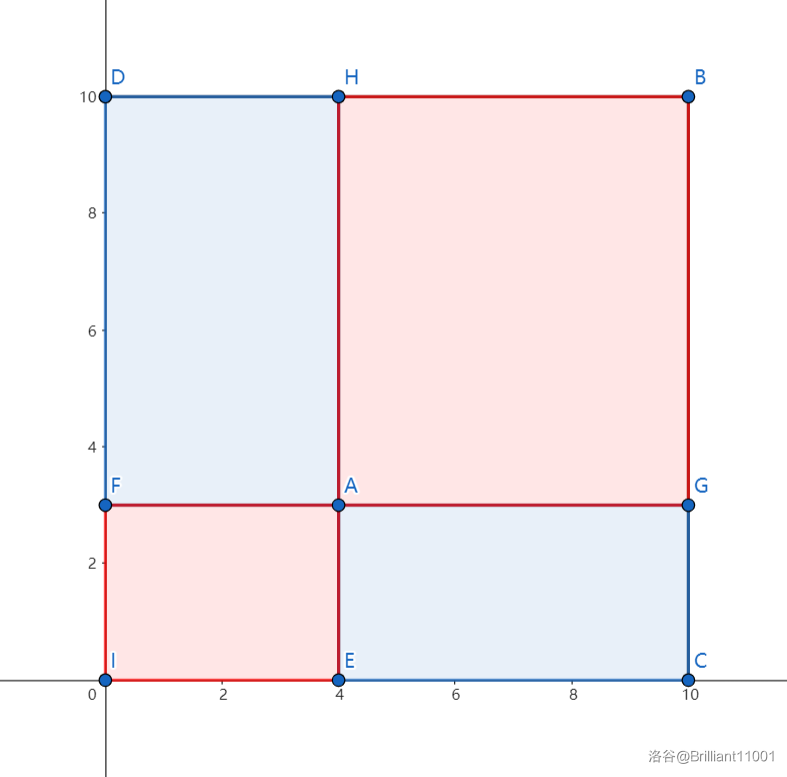
其中四边形 \(\text{AGBH}\) 是我们要求的。

设此询问为 \(\{x1, y1, x2, y2\}\)
\(A(x1 - 1, y1 - 1)\)
\(E(x1 - 1, y2)\)
\(G(x2, y1 - 1)\)
\(B(x2, y2)\)

设左下角为 \((0, 0)\)，右上角为 \((i, j)\) 的矩形中点的数量为 \(sum_{i, j}\)。

所以我们要求的是 \(sum_{x2, y2} + sum_{x1 - 1, y1 - 1} - sum_{x1 - 1, y2} - sum_{x2, y1 - 1}\)。

将询问分成四个部分，分别存 \(A,E,G,B\) 四个，然后将给定的点和询问都按照 \(x\) 升序排列，这样 \(x\) 的限制就可以不用管了，再建立一个树状数组来维护 \(y\) 即可。

需要注意的几个点：

1. 本题值域较大，需要离散化；（其实也没有那么大，不离散化也能过）
2. 离散化后的数要从 \(1\) 开始，因为为 \(0\) 的话树状数组会死循环；
3. 询问要分成 \(4\) 份，也就是说要开 \(4\) 倍空间，同理，树状数组的值域也要开大点。

\(\texttt{Code:}\)

#include <vector>
#include <iostream>
#include <algorithm>

#define lowbit(x) x & -x
using namespace std;

const int N = 500010, M = 20000010;

int n, m;
struct BIT{
    int c[M];
    void add(int x, int y) {
        for(; x < M; x += lowbit(x)) c[x] += y;
    }
    int ask(int x) {
        int res = 0;
        for(; x; x -= lowbit(x)) res += c[x];
        return res; 
    }
}tr;
vector<int> nums;
struct node{
    int id, x, y, sign;
    bool operator< (const node &o) const {
        return x < o.x;
    }
}q[N << 2];
int tt;
struct Point{
    int x, y;
    bool operator< (const Point &o) const {
        return x < o.x;
    }
}a[N];
int ans[N];

int find(int x) {
    return lower_bound(nums.begin(), nums.end(), x) - nums.begin() + 1;
}

int main() {
    scanf("%d%d", &n, &m);
    int x, y;
    for(int i = 1; i <= n; i++) {
        scanf("%d%d", &x, &y);
        a[i] = {x, y};
        nums.push_back(y);
    }
    int x1, y1, x2, y2;
    for(int i = 1; i <= m; i++) {
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        q[++tt] = {i, x1 - 1, y1 - 1, 1};
        q[++tt] = {i, x1 - 1, y2, -1};
        q[++tt] = {i, x2, y1 - 1, -1};
        q[++tt] = {i, x2, y2, 1};
        nums.push_back(y1 - 1), nums.push_back(y2);
    }
    sort(nums.begin(), nums.end());
    nums.erase(unique(nums.begin(), nums.end()), nums.end());
    sort(a + 1, a + n + 1);
    sort(q + 1, q + tt + 1);
    int id = 1;
    for(int i = 1; i <= tt; i++) {
        while(a[id].x <= q[i].x && id <= n) tr.add(find(a[id++].y), 1);
        ans[q[i].id] += q[i].sign * tr.ask(find(q[i].y));
    }
    for(int i = 1; i <= m; i++)
        printf("%d\n", ans[i]);
    return 0;
}