状态机模型 dp
\(\texttt{0x00}\) 状态机介绍
简单来说，状态机就是一个数学模型，不是一个实际的机器。它含有几个状态，还有几个函数（或者通俗一点叫“桥梁”），使得这几种状态可以在一定条件下实现相互转化。
是不是和动态规划的状态转移过程很像？
所以有一类型的动态规划题目，它的状态可以在一定的条件下相互转化，这时从状态机的角度来分析会比较好想。
\(\texttt{0x01}\) 例题
一. \(01\) 两种状态
AcWing 1049. 大盗阿福
题目描述
街道上有 \(N\) 家店铺，按照顺序从 \(1\) 到 \(N\) 排好，
第 \(i\) 家店铺的财产是 \(w_i\)，大盗阿福如果偷了第 \(i\) 家店铺，则他不能偷相邻的店铺，否则会被抓起来。
帮助大盗阿福找出一种偷盗方案，使得获得的总财产最大。
思路
从一般的 dp 思路来思考：
设 \(f(i)\) 表示偷了前 \(i\) 家店铺能获得的最大财产，对于第 \(i\) 家店铺，可以选择偷或不偷，若偷，则第 \(i - 1\) 家店铺就不能偷则应该从 \(f(i - 2)\) 转移过来；不偷，则由 \(f(i - 1)\) 转移过来。
综上，状态转移方程为：
从状态机的角度思考：
根据题意，可以总结出两种状态：偷了上一家店铺，没偷上一家店铺。
状态 \(1\) 可以由状态 \(2\) 转移过来，但不能由它自己转移过来（因为不能偷两家相邻的店铺）。
状态 \(2\) 既可以由状态 \(1\) 转移过来，也可以由它自己转移过来。
画个图就是这样的：
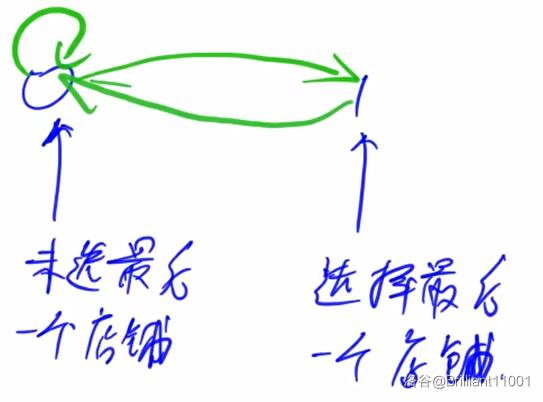
设 \(f(i, 0)\) 表示偷前 \(i\) 家店铺且不偷第 \(i\) 家店铺能获得的最大财产，\(f(i, 1)\) 表示偷前 \(i\) 家店铺且偷第 \(i\) 家店铺能获得的最大财产，则状态转移方程为：
发现每层状态只会由他的上一层状态得到，所以可以加滚动数组优化。
\(\texttt{Code:}\)
#include <iostream>
using namespace std;
int T;
int n, a;
int f[2][2];
int main() {
scanf("%d", &T);
while(T--) {
scanf("%d", &n);
f[0][0] = f[0][1] = 0;
for(int i = 1; i <= n; i++) {
scanf("%d", &a);
f[i & 1][0] = max(f[i - 1 & 1][0], f[i - 1 & 1][1]);
f[i & 1][1] = f[i - 1 & 1][0] + a;
}
printf("%d\n", max(f[n & 1][0], f[n & 1][1]));
}
return 0;
}
AcWing 1057. 股票买卖 IV
题目大意：
给定一个长度为 \(N\) 的数组，数组中的第 \(i\) 个数字表示一个给定股票在第 \(i\) 天的价格。
你最多可以完成 \(k\) 笔交易，求能获取的最大利润。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。
思路：
这道题用一般的方法分析就不太容易了，直接用状态机的思路分析。
不难总结出这道题有两种状态：持股 \((1)\) 和不持股 \((0)\)。
操作可分为四种：
- 买入行为：\(k=0 \rightarrow k=1\)
- 卖出行为：\(k=1 \rightarrow k=0\)
- 持仓行为：\(k=1 \rightarrow k=1\)
- 空仓行为：\(k=0 \rightarrow k=0\)
画图就是这样的：
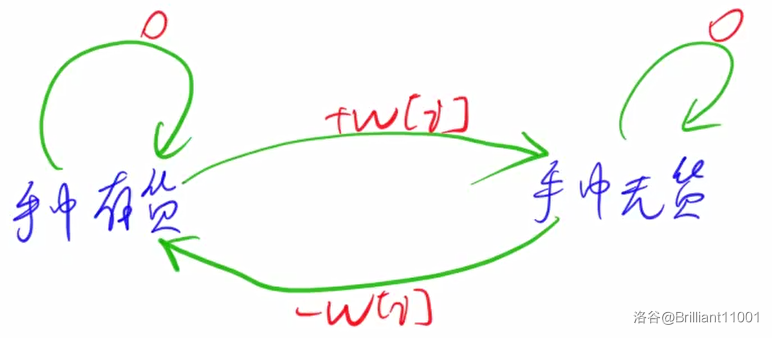
令 \(f(i, j, k)\) 表示：考虑前 \(i\) 天的股票，第 \(i\) 天的决策是 \(k\)，且完成的完整交易数为 \(j\) 的方案。
状态转移方程为：
注意：因为一次买入卖出合为一笔交易，这里将买入算作开始一次交易，所以要消耗性次数，而卖出是一次交易的结束，不消耗次数。
同样可以加滚动数组优化。
\(\texttt{Code:}\)
#include <cstring>
#include <iostream>
using namespace std;
const int N = 100010, M = 110;
int n, k;
int a[N];
int dp[2][M][2];
int ans;
int main() {
scanf("%d%d", &n, &k);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
memset(dp, -0x3f, sizeof dp);
dp[0][0][0] = dp[1][0][0] = 0;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= min(i, k); j++) {
dp[i & 1][j][0] = max(dp[i - 1 & 1][j][0], dp[i - 1 & 1][j][1] + a[i]);
dp[i & 1][j][1] = max(dp[i - 1 & 1][j][1], dp[i - 1 & 1][j - 1][0] - a[i]);
ans = max(ans, max(dp[i & 1][j][0], dp[i & 1][j][1]));
}
}
printf("%d", ans);
return 0;
}
P1352 没有上司的舞会
题目大意
给定一棵有 \(n\) 个节点的树，每个节点有一个权值 \(w_i\)，现在要从这棵树上选出一些节点。若选择了一个节点，那么它的子节点就不能被选，问能获得的最大权值和。
思路
令 \(f(i)\) 为以 \(i\) 为根的子树能获得的最大权值和，那么很明显，我们应该先算儿子子树的 \(f\) 值，然后才能算 \(f(i)\)，更新顺序为从下往上。
但是如果我们这样设计状态会发现无法转移——你不知道当前儿子节点的 \(f\) 是选儿子得到的还是没选得到的，所以你也就无法确定节点 \(i\) 选还是不选。
根据状态机的思路，本题有两个状态：选当前节点 \((1)\) 和不选当前节点 \((0)\)。
选当前节点的前提是不能选儿子，\(0\rightarrow 1\)。
不选当前节点那么两种都能转移，\(1\rightarrow 0,0\rightarrow 0\)
令 \(f(i, j)\) 表示考虑以 \(i\) 为根的子树且 \(i\) 的策略为 \(j\) 能获得的最大权值和，则状态转移方程为：
其中 \(j\) 是 \(i\) 的子节点。
然后就可以快乐地树上递归转移了。
\(\texttt{Code:}\)
#include <cstring>
#include <iostream>
using namespace std;
const int N = 6010;
typedef long long ll;
int n, ori;
int h[N], e[N], ne[N], idx;
int w[N], f[N][2]; //0 不选，1 选
bool have_father[N];
int root;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dp(int u) {
f[u][1] = w[u];
for(int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
dp(j);
f[u][0] += max(f[j][0], f[j][1]);
f[u][1] += f[j][0];
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", &w[i]);
int a, b;
for(int i = 1; i < n; i++) {
scanf("%d%d", &a, &b);
add(b, a);
have_father[a] = true;
}
for(int i = 1; i <= n; i++)
if(!have_father[i]) {
root = i;
break;
}
dp(root);
printf("%d", max(f[root][0], f[root][1]));
return 0;
}
二. 多种状态
AcWing 1058. 股票买卖 V
题目大意：
给定一个长度为 \(N\) 的数组，数组中的第 \(i\) 个数字表示一个给定股票在第 \(i\) 天的价格。
注意：
- 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。
- 卖出股票后，无法在第二天买入股票（冷冻期为 \(1\) 天）。
求能获得的最大利润。
思路：
这道题的状态不再是简单的 \(01\) 状态。
但还是一样，可以归纳为 \(3\) 种状态：持股 \((0)\)、冷冻期 \((1)\)、未持股 \((2)\)。
操作可分为五种：
- 买入行为：\(2 \rightarrow 0\)
- 卖出行为：\(0 \rightarrow 1\)
- 持仓行为：\(0 \rightarrow 0\)
- 空仓行为：\(2 \rightarrow 2\)
- 冷冻期结束：\(1 \rightarrow 2\)
画图来看就是这样：
设 \(f(i, j)\) 表示考虑前 \(i\) 天的股票且在第 \(i\) 天时是状态 \(j\) 的最大利润。
则状态转移方程为：
\(\texttt{Code:}\)
#include <cstring>
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int dp[N][3];
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
memset(dp, -0x3f, sizeof dp);
for(int i = 0; i <= n; i++) dp[i][2] = 0;
for(int i = 1; i <= n; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][2] - a[i]);
dp[i][1] = dp[i - 1][0] + a[i];
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1]);
}
printf("%d", max(dp[n][1], dp[n][2]));
return 0;
}
AcWing 1052. 设计密码
题目大意
你现在需要设计一个密码 \(S\)，满足：
- \(S\) 的长度是 \(N\)；
- \(S\) 只包含小写英文字母；
- \(S\) 不包含子串 \(T\)；
请问共有多少种不同的密码满足要求？
由于答案会非常大，请输出答案模 \(10^9+7\) 的余数。
思路
考虑从前向后构造密码，所以可以将目前构造到第几位作为阶段来 dp。
模板串不能作为字串出现在密码中，考虑 KMP 的过程，可以将目前匹配到了模板串的第几位作为第二维。
设 \(f(i, j)\) 表示目前构造到 \(i\) 位且第 \(i\) 位匹配到模板串的第 \(j\) 位的密码数。
由题可知，不能匹配到第 \(|T|\) 位，所以答案应该为 \(\sum\limits_{0 \le j < |T|}\{f(n, j)\}\)。
接下来考虑状态转移。
首先需要了解一下自动机的概念。
这道题考虑一个状态能更新那些状态要好想很多。
假设我们现在已经构造好了前 \(i\) 位，要去构造第 \(i + 1\) 位了。因为第 \(i + 1\) 位可以放 \(26\) 种字母，而每种字母都会有不同的匹配的结果，所以共有 \(26\) 种状态。
然后枚举第 \(i + 1\) 位的字母，对每个字母找到能匹配的最大后缀长度 \(\delta(\pi (i), ch_{i + 1})\)，即构造第 \(i + 1\) 位后该密码能匹配到的模板串中的位置，也就找到了状态 \(j\) 应该更新的状态。
综上所述，状态转移方程为：
\(\texttt{Code:}\)
#include <cstring>
#include <iostream>
using namespace std;
const int N = 55, mod = 1e9 + 7;
int n, len;
char s[N];
int dp[N][N];
int ne[N];
int main() {
scanf("%d%s", &n, s + 1);
len = strlen(s + 1);
//预处理 ne 数组
for(int i = 2, j = 0; i <= len; i++) {
while(j && s[j + 1] != s[i]) j = ne[j];
if(s[j + 1] == s[i]) j++;
ne[i] = j;
}
dp[0][0] = 1;
for(int i = 0; i < n; i++)
for(int j = 0; j < len; j++)
for(char k = 'a'; k <= 'z'; k++) {
//计算应该更新的状态
int tmp = j;
while(tmp && s[tmp + 1] != k) tmp = ne[tmp];
if(s[tmp + 1] == k) tmp++;
if(tmp < len) dp[i + 1][tmp] = (dp[i + 1][tmp] + dp[i][j]) % mod;
}
int res = 0;
for(int i = 0; i < len; i++) res = (res + dp[n][i]) % mod;
printf("%d", res);
return 0;
}
