树上公共祖先（LCA）
\(\texttt{0x00}\) 概念
给定一棵有根树，若节点 \(z\) 既是节点 \(x\) 的祖先，又是 \(y\) 的祖先，则称 \(z\) 是 \(x,y\) 的公共祖先。在 \(x,y\) 的所有公共祖先中，深度最大的一个称为 \(x,y\) 的最近公共祖先，记为 \(\texttt{LCA(x,y)}\)。
\(\texttt{0x01}\) 求解方法
1. 树上倍增法
思路：
由向上标记法优化而来。
向上标记法是每次向上走一步，效率较低。而树上倍增法优化了“走”的过程，每次向上走 \(2^k\) 辈祖先，然后根据二进制拆分思想求解。
设 \(f[x][k]\) 是 \(x\) 的 \(2^k\) 辈祖先，根据动态规划的思想，则可以得到状态转移方程：
其中 \(k\in [1,\log n]\)。
节点的深度为动态规划的“阶段”，所以应该对树执行广度优先遍历，按照层次顺序，在节点入队前，计算它对应的 \(f\) 数组的值。
这样，就可以在 \(O(n\log n)\) 的时间内预处理出 \(f\) 数组。
对于每组询问 \((x,y)\)，我们再利用二进制的思想，将这两个点中深度大的那个点向上走，直到两个点深度相同。
此时，如果节点 \(x\) 和 \(y\) 在同一条树链上，就会相遇，此时直接返回 \(x\)。
否则，再将 \(x\) 和 \(y\) 同时向上走相同的距离，即依次尝试走 \(k = 2^{\log n},\cdots,2^1,2^0\) 步，在每次尝试中，若 \(f[x][k] \ne f[y][k]\)（即仍未相遇），则令 \(x = f[x][k],y = f[y][k]\)。
此时 \(x,y\) 必定只差一步就相遇了，它们的父节点 \(f[x][0]\) 就是 \(\operatorname{LCA(x,y)}\)。
综上所述，树上倍增法求 \(\operatorname{LCA}\) 的预处理为 \(O(n\log n)\)，每次询问为 \(O(\log n)\)。
\(\texttt{Code:}\)
void bfs(int s) {
queue<int> q;
q.push(s);
dep[s] = 1;
while(q.size()) {
int t = q.front();
q.pop();
for(int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if(dep[j]) continue;
dep[j] = dep[t] + 1;
f[j][0] = t;
for(int k = 1; k <= T; k++) f[j][k] = f[f[j][k - 1]][k - 1];
q.push(j);
}
}
}
int lca(int x, int y) {
if(dep[x] > dep[y]) swap(x, y);
for(int i = T; i >= 0; i--) {
if(dep[f[y][i]] >= dep[x]) y = f[y][i];
}
if(x == y) return x;
for(int i = T; i >= 0; i--) {
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
}
return f[x][0];
}
2.tarjan 算法
本质上也是对向上标记法的优化。它是个离线算法，所以局限性很大，很不常用。
思路：
在深度优先遍历的任意时刻，树中的节点分为 \(3\) 类。
- 已经访问且回溯的节点。这些节点标记为 \(2\)；
- 已经访问过但还没回溯的节点，此时这些节点就是正在访问的节点 \(x\) 或 \(x\) 的祖先。这些节点标记为 \(1\)；
- 尚未访问的节点。这些节点标记为 \(0\)。
这样，对于正在访问的节点 \(x\)，它到根节点的路径已经标记为 \(1\)。
若 \(y\) 是已经访问完毕并且正在回溯的点，则 \(\operatorname{LCA(x,y)}\) 就是从 \(y\) 向上走到根，第一个遇到的标记为 \(1\) 的节点。
可以用并查集优化这个操作，当一个节点被标记为 \(2\) 时，把它所在的集合合并到它的父节点所在的集合中（合并时它的父节点标记一定为 \(1\)，且单独构成一个集合）。
所以查询 \(y\) 所在集合的代表元素就等价于求 \(\operatorname{LCA(x,y)}\)。
在 \(x\) 回溯之前，扫描与 \(x\) 相关的所有询问，若询问中的另一个点 \(y\) 的标记为 \(2\)，答案即为 \(\operatorname{find(y)}\)。
时间复杂度为 \(O(n + m)\)。
\(\texttt{Code:}\)
#include <cmath>
#include <vector>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 500010;
typedef pair<int, int> PII;
int n, m, root;
int h[N], e[N << 1], w[N << 1], ne[N << 1], idx;
int dist[N];
int ans[N];
vector<PII> que[N];
int st[N];
int p[N];
int find(int x) {
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void add_query(int a, int b, int id) {
que[a].push_back({b, id});
que[b].push_back({a, id});
//注意两边都要 push，因为可能在更新其中之一时另一个点未被标记成 2，导致未计算答案
}
void tarjan(int u) {
st[u] = 1;
for(int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if(st[j]) continue;
tarjan(j);
p[j] = u;
}
for(int i = 0; i < que[u].size(); i++) {
int j = que[u][i].first, id = que[u][i].second;
if(st[j] == 2) ans[id] = find(j);
}
++st[u];
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d%d", &n, &m, &root);
int a, b;
for(int i = 1; i < n; i++) {
scanf("%d%d", &a, &b);
add(a, b)， add(b, a);
}
for(int i = 1; i <= m; i++) {
scanf("%d%d", &a, &b);
if(a != b) add_query(a, b, i);
else ans[i] = a;
}
for(int i = 1; i <= n; i++) p[i] = i;
tarjan(root);
for(int i = 1; i <= m; i++) printf("%d\n", ans[i]);
return 0;
}
\(\texttt{0x02}\) 一些例题
一. 利用树的性质求 LCA 维护信息
题目大意：
给定一棵树，\(m\) 次询问树上任意两点的距离。
思路：
在树上，两点之间的路径唯一，即：\(x\) 到 \(y\) 的路径为 \(x\to lca(x,y)\to y\)。
再加上距离具有结合律，所以我们可以在求 LCA 时顺便处理出根节点到所有节点的距离。
这样对于每个询问 \((x,y)\)，答案为：
再加上一些小细节即可。
\(\texttt{Code:}\)
#include <cmath>
#include <queue>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 100010;
int n, m, T;
int h[N], e[N << 1], ne[N << 1], idx;
int f[N][25], dep[N];
int v[N];
int dist[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void bfs(int s) {
queue<int> q;
q.push(s);
dep[s] = 1, dist[s] = v[s];
while(q.size()) {
int t = q.front();
q.pop();
for(int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if(dep[j]) continue;
dep[j] = dep[t] + 1;
f[j][0] = t;
dist[j] = v[j] + dist[t];
for(int k = 1; k <= T; k++) f[j][k] = f[f[j][k - 1]][k - 1];
q.push(j);
}
}
}
int lca(int x, int y) {
if(dep[x] > dep[y]) swap(x, y);
for(int i = T; i >= 0; i--)
if(dep[f[y][i]] >= dep[x]) y = f[y][i];
if(x == y) return x;
for(int i = T; i >= 0; i--)
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
T = (int)log2(n);
int a, b;
for(int i = 1; i < n; i++) {
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
++v[a], ++v[b];
}
bfs(1);
while(m--) {
scanf("%d%d", &a, &b);
int p = lca(a, b);
printf("%d\n", dist[a] + dist[b] - 2 * dist[p] + v[p]);
}
return 0;
}
P5836 [USACO19DEC] Milk Visits S
题目大意：
给定一棵树，树上每一个节点都有一个类型为 \(0\) 或 \(1\) 的物品。
\(m\) 次询问，回答任意两点之间的路径上是否有某种物品。
思路：
考虑到倍增 LCA 能预处理出类似于前缀和的数据，维护具有结合率的信息，所以提前处理出根节点到所有点的路径上两种物品的数目各是多少，然后用类似求距离的方法维护。
题目大意：
给定一棵树，\(m\) 次询问，回答任意两点之间的路径上所有节点深度的 \(k\) 次方和。
思路：
注意到 \(k \le 50\)，所以可以把所有的 \(k\) 值都预处理出来，然后维护即可。
注意：为防止对负数取模，在取模之前要加上模数！
二. 树上差分
题目大意：
给定一棵树，\(m\) 次操作，每次给定 \((x,y)\)，覆盖树上 \(x\to y\) 的路径上的点，最后输出树上被覆盖次数最多的节点的被覆盖次数。
思路：
考虑暴力，对于每个操作 \((x,y)\)，求出 \(\operatorname{LCA(x,y)}\)，从 \(x\) 走到 \(\operatorname{LCA(x,y)}\)，再从 \(\operatorname{LCA(x,y)}\) 走到 \(y\)，给经过的节点都加上 \(1\)，最后统计最大值。时间复杂度最坏为 \(O(nm)\)。
其实这种操作很像 DS 中的区间加操作，又因为这是个静态问题，所以可以树上差分。
树上差分类似于序列上的差分，想象一下把 \(\operatorname{LCA(x,y)}\to x\) 和 \(\operatorname{LCA(x,y)}\to y\) 拆成两条链，然后左端点 \(+1\)，右端点 \(-1\) 即可。
如图所示：
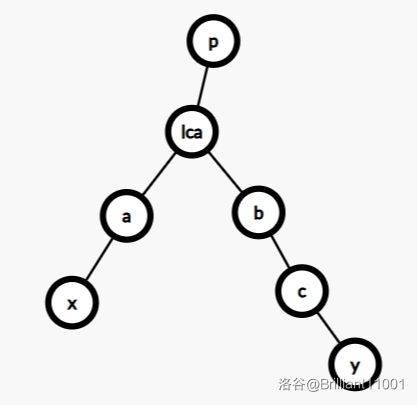
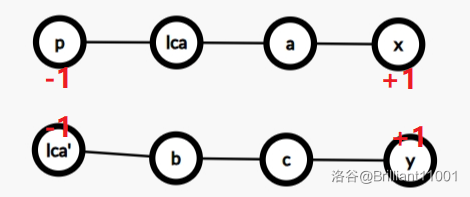
好丑
这样操作之后，每个节点的子树的大小就是该点的被覆盖次数。
\(\texttt{Code:}\)
#include <cmath>
#include <queue>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 50010;
int n, m, T;
int h[N], e[N << 1], ne[N << 1], idx;
int dep[N];
int f[N][22];
int siz[N], v[N];
int ans;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void bfs(int s) {
queue<int> q;
q.push(s);
dep[s] = 1;
while(q.size()) {
int t = q.front();
q.pop();
for(int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if(dep[j]) continue;
dep[j] = dep[t] + 1;
f[j][0] = t;
for(int k = 1; k <= T; k++) f[j][k] = f[f[j][k - 1]][k - 1];
q.push(j);
}
}
}
int LCA(int x, int y) {
if(dep[x] > dep[y]) swap(x, y);
for(int i = T; i >= 0; i--)
if(dep[f[y][i]] >= dep[x]) y = f[y][i];
if(x == y) return x;
for(int i = T; i >= 0; i--)
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
int dfs(int u, int fa) {
siz[u] = v[u];
for(int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if(j == fa) continue;
siz[u] += dfs(j, u);
}
return siz[u];
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
T = (int)log2(n);
int a, b;
for(int i = 1; i < n; i++) {
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
bfs(1);
while(m--) {
scanf("%d%d", &a, &b);
int lca = LCA(a, b);
++v[a], ++v[b], --v[lca], --v[f[lca][0]];
}
dfs(1, -1);
for(int i = 1; i <= n; i++) ans = max(ans, siz[i]);
printf("%d\n", ans);
return 0;
}
题目大意：
给定一棵树，要求按顺序走完给定的所有点，每移动一步就要给这次移动经过的点增加 \(1\) 的点权，且路径的终点不增加点权。求每一个点的最小点权。
和上一道题十分相似，只需注意最后一个点的 \(siz\) 要减一。
P6869 [COCI2019-2020#5] Putovanje
题目大意：
求按节点编号顺序遍历一棵树的最小费用，边权分成单程票和多程票两种。
思路：
把每条边算作附属于它下面的点（深度更大的点），然后用树上差分求出每条边的经过次数，比较单程票和多程票费用。
只需注意处理每条边在附属过后在原来费用数组中的位置即可。
三. 树上问题分类讨论
很有意思的一道分讨题。
题目大意：
给定一棵树，\(m\) 次询问 \((a,b,c,d)\)，回答 \(a\to b\) 与 \(c\to d\) 是否相交。
先将两条路径拆开，得到 \(4\) 条链：
不难看出，这两条路径相交当且仅当这 \(4\) 条链有两条相交。
(1) ① 与 ③ 相交
如图：
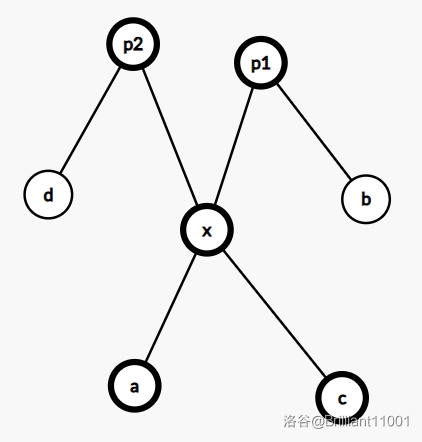
(2) ① 与 ④ 相交
如图：
(3) ② 与 ③ 相交
如图：
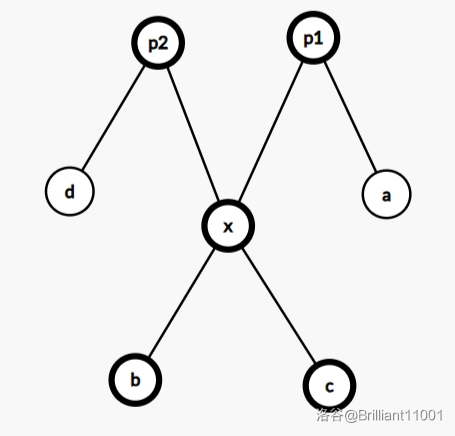
(4) ② 与 ④ 相交
如图：
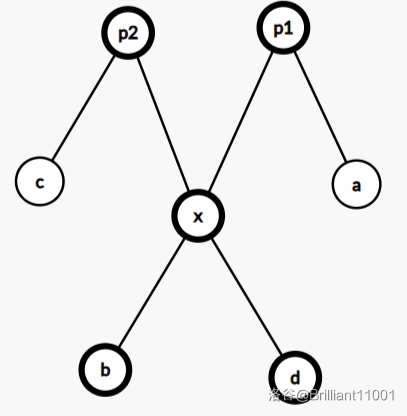
最后综合一下就能写出 \(\operatorname{check}\) 函数。
inline bool check(int a, int b, int c, int d) {
int x = lca(a, b), y = lca(c, d), p1 = lca(a, c), p2 = lca(a, d), p3 = lca(b, c), p4 = lca(b, d);
if(lca(p1, d) == y && lca(p1, b) == x) return true;
if(lca(p2, c) == y && lca(p2, b) == x) return true;
if(lca(p3, d) == y && lca(p3, a) == x) return true;
if(lca(p4, c) == y && lca(p4, a) == x) return true;
return false;
}
题目大意：
给定一棵树，\(m\) 次询问，每次 \(3\) 个点 \((x,y,z)\)，回答与这 \(3\) 个点距离和最小的点及距离和。
首先思考什么点是距离和最小的点。
不难发现，如果随便选一个点，那么有些边可能要重复走几遍，而如果选择三个点互相通达的简单路径上的一个点，那么就没有边被重复走过。
直接讲有点抽象，如图：
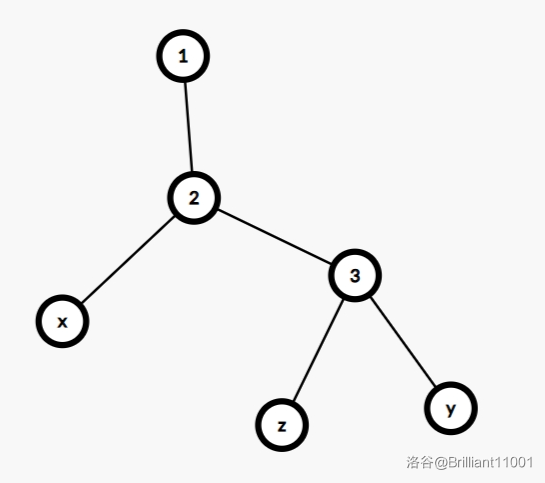
若选择 \(2\)，则 \(2-3\) 这条边会被走 \(2\) 次，不是最短。
若选择 \(3\)，则所有边都只会走一次，此时为最短。
而 \(3\) 就在三个点互相通达的简单路径上。
多画几个图，总结出：选择三个点 LCA 中深度最大的那个点是最优的。
此时最小距离为：
四. LCA 综合运用
题目大意：
给定一张无向图，\(m\) 次询问，每次询问 \(x\) 到 \(y\) 的所有路径中最小的那条边的边权最大是多少。
根据贪心思想，我们肯定优先选择边权大的边走，这启示我们可以先求一遍原无向图的最大生成树，去掉永远也不会走过的边。
利用 \(\texttt{kruskal}\) 算法得到原无向图的一个最大生成森林。若 \(x\) 和 \(y\) 不在一个连通块，就直接输出 \(-1\)。
否则就转化成了树上问题，等价于求两点之间路径中的边权最小值，默写模板即可。
\(\texttt{Code:}\)
#include <queue>
#include <cmath>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010, M = 25, E = 50010;
typedef long long ll;
typedef pair<int, int> PII;
int n, m, q, T;
int h[N], e[N << 1], ne[N << 1], w[N << 1], idx;
int f[N][M], dep[N];
int mind[N][M];
struct node{
int a, b, w;
bool operator < (const node &o) const {
return w > o.w;
}
}edges[M];
int p[N];
int cnt;
vector<int> uni[N];
int v[N];
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int find(int x) {
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
void kruskal() {
for(int i = 1; i <= n; i++) p[i] = i;
sort(edges + 1, edges + m + 1);
for(int i = 1; i <= m; i++) {
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
int x = find(a), y = find(b);
if(x != y) {
p[x] = y;
add(a, b, w), add(b, a, w);
}
}
}
void dfs(int u) {
v[u] = cnt;
uni[cnt].push_back(u);
for(int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if(v[j]) continue;
dfs(j);
}
}
void bfs(int s) {
queue<int> q;
q.push(s);
for(int i = 1; i <= n; i++) {
if(dep[i]) continue;
for(int j = 0; j <= T; j++)
mind[i][j] = 0x3f3f3f3f;
}
dep[s] = 1;
while(q.size()) {
int t = q.front();
q.pop();
for(int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if(dep[j]) continue;
dep[j] = dep[t] + 1;
f[j][0] = t;
mind[j][0] = w[i];
// printf("------%d\n", mind[j][0]);
for(int k = 1; k <= T; k++) {
f[j][k] = f[f[j][k - 1]][k - 1];
mind[j][k] = min(mind[j][k - 1], mind[f[j][k - 1]][k - 1]);
}
q.push(j);
}
}
}
int lca(int x, int y) {
int res = 0x3f3f3f3f;
if(dep[x] > dep[y]) swap(x, y);
for(int i = T; i >= 0; i--)
if(dep[f[y][i]] >= dep[x]) {
res = min(res, mind[y][i]);
y = f[y][i];
}
if(x == y) return res;
for(int i = T; i >= 0; i--)
if(f[x][i] != f[y][i]) {
res = min(res, min(mind[x][i], mind[y][i]));
x = f[x][i], y = f[y][i];
}
res = min(res, min(mind[x][0], mind[y][0]));
return res;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
T = (int)log2(n);
int a, b, c;
for(int i = 1; i <= m; i++) {
scanf("%d%d%d", &a, &b, &c);
edges[i] = {a, b, c};
}
kruskal();
for(int i = 1; i <= n; i++)
if(!v[i]) {
cnt++;
dfs(i);
}
for(int i = 1; i <= cnt; i++) bfs(uni[i][0]);
scanf("%d", &q);
while(q--) {
scanf("%d%d", &a, &b);
if(v[a] != v[b]) puts("-1");
else {
printf("%d\n", lca(a, b));
}
}
return 0;
}
