高贵的伸展树——Splay
伸展树,也叫
定义
struct node {
int s[2], p, v; //左右儿子,父亲,权值
int siz; //子树大小
void init(int _p, int _v) { //初始化函数
s[0] = s[1] = 0;
p = _p, v = _v;
siz = 1;
}
}tr[N];
1. 基本操作:旋转
首先
就比如:

先改变
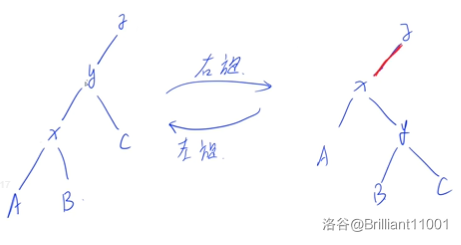
先改变
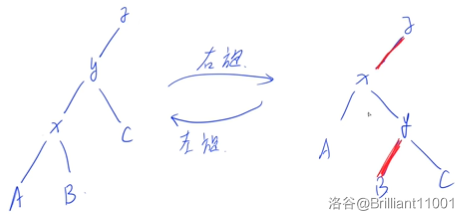
先改变
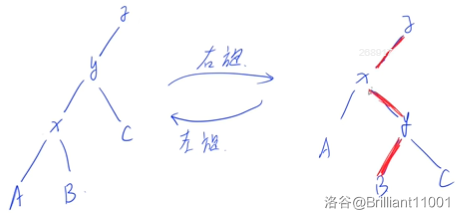
由这三幅图就能很形象地展示旋转后信息的变化了。
代码:
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = x == tr[y].s[1]; //k 表示 x 是 y 的哪个儿子
tr[z].s[y == tr[z].s[1]] = x, tr[x].p = z; //更新 x 和 z 之间的边
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y; //更新 y 和 x 的另一儿子之间的边
tr[x].s[k ^ 1] = y, tr[y].p = x; //更新 x 和 y 之间的边
}
2. 核心操作:
这里运用了局部性原理,就是说如果某一次用到了某节点,那么后面还可能再用到它 (听起来十分玄学)。对于这一点有详细的证明,这里就不放了。
例如
在这个转移的过程中,有两种情况,一种呈直线,另一种呈折线,如下图:

对于第一种情况,先转
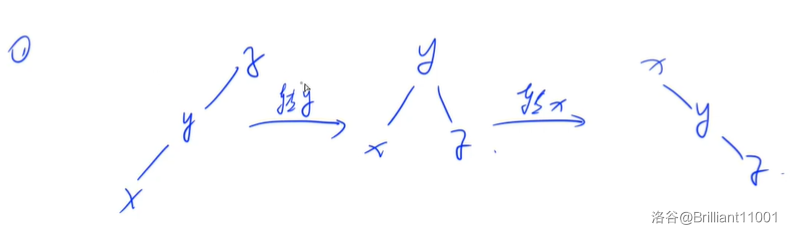
对于第二种情况,转两次
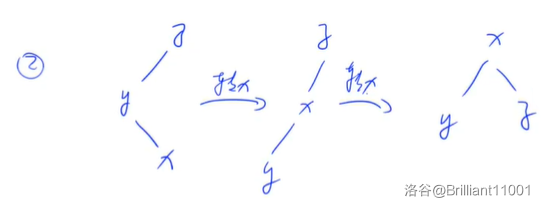
代码:
void splay(int x, int k) {
while(tr[x].p != k) { //一直转直到 x 被转到 k 下方
int y = tr[x].p, z = tr[y].p;
if(z != k) { //如果爷爷节点不是目标节点则转两次,否则转一次
if((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x); //直线,转两次 x
else rotate(y); //折线转 x,再转 y
}
rotate(x);
}
if(!k) root = x; //若是将 x 转到根,那么 x 就是新的根
}
3. 插入
若是单点插入则与二叉搜索树雷同,这里不再赘述。
代码:
void insert(int v) {
int u = root, p = 0;
while(u) p = u, u = tr[u].s[v > tr[u].v]; //小于走左边,大于走右边
u = ++idx; //分配一个新结点
if(p) tr[p].s[v > tr[p].v] = u;
tr[u].init(p, v);
splay(u, 0); //注意每次操作完要将该节点转到根
}
若是在某个位置

4. 删除
删除也是同理,若要删除
void remove(int v) {
int la = get_next(v, 0);
int ne = get_next(v, 1);
splay(la, 0), splay(ne, la);
int del = tr[ne].s[0];
if(tr[del].cnt > 1) {
tr[del].cnt--;
splay(del, 0);
}
else tr[ne].s[0] = 0;
}

5. 找前驱/后继
代码:
void find(int v) { //查找值为v的位置
int u = root;
if(!u) return ;
while(tr[u].s[v > tr[u].v] && v != tr[u].v) //判断其左右儿子是否存在
u = tr[u].s[v > tr[u].v]; //获得一个等于x或最接近x的节点
splay(u, 0); //splay保证复杂度的关键
}
int get_next(int v, int f){ //查找前驱/后继,f = 0找前驱, = 1找后继
find(v);
int u = root;
if((tr[u].v > v && f) || (tr[u].v < v && !f)) return u;
u = tr[u].s[f];
while(tr[u].s[f ^ 1]) u = tr[u].s[f ^ 1];
return u;
}
6. 求
int get_rank(int v) {
insert(v), find(v);
int res = tr[tr[root].s[0]].siz;
remove(v); //因为可能 v 不在平衡树中,所以要先插入一个虚拟节点方便查询,再删除
return res;
}
7. 求排名
int get_k(int k) { //查找排名为k的值
int u = root;
if(tr[u].siz < k) return 0;
while(1) {
int left = tr[u].s[0];
if(tr[left].siz >= k) u = left;
else if(tr[left].siz + tr[u].cnt < k){
k -= tr[left].siz + tr[u].cnt;
u = tr[u].s[1];
}
else return tr[u].v;
}
return -1;
}
8. 维护信息
在查询第
inline void pushup(int x) {tr[x].siz = tr[tr[x].s[0]].siz + tr[tr[x].s[1]].siz + tr[x].cnt;}
对于一些有区间修改的题(下面会讲到)也需要用到和线段树一样的懒标记来维护信息,这让线段树直接哭晕在厕所,同样,用一个
组合一下就是这道模板题了:
P3369 【模板】普通平衡树
#include <iostream>
using namespace std;
const int N = 500010, INF = 0x3f3f3f3f;
int n;
struct node {
int s[2], p, v;
int siz, cnt;
void init(int _p, int _v) {
p = _p, v = _v;
siz = cnt = 1;
}
}tr[N];
int root, idx;
inline void pushup(int x) {tr[x].siz = tr[tr[x].s[0]].siz + tr[tr[x].s[1]].siz + tr[x].cnt;}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = x == tr[y].s[1];
tr[z].s[y == tr[z].s[1]] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
void splay(int x, int k) {
while(tr[x].p != k) {
int y = tr[x].p, z = tr[y].p;
if(z != k) {
if((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!k) root = x;
}
void insert(int v) {
int u = root, p = 0;
while(u && v != tr[u].v) p = u, u = tr[u].s[v > tr[u].v];
if(u) tr[u].cnt++;
else {
u = ++idx;
if(p) tr[p].s[v > tr[p].v] = u;
tr[u].init(p, v);
}
splay(u, 0);
}
void find(int v) { //查找值为v的位置
int u = root;
if(!u) return ;
while(tr[u].s[v > tr[u].v] && v != tr[u].v) //判断其左右儿子是否存在
u = tr[u].s[v > tr[u].v]; //获得一个等于x或最接近x的节点
splay(u, 0); //splay保证复杂度的关键
}
int get_next(int v, int f){ //查找前驱/后继
find(v);
int u = root;
if((tr[u].v > v && f) || (tr[u].v < v && !f)) return u;
u = tr[u].s[f];
while(tr[u].s[f ^ 1]) u = tr[u].s[f ^ 1];
return u;
}
void remove(int v) {
int la = get_next(v, 0);
int ne = get_next(v, 1);
splay(la, 0), splay(ne, la);
int del = tr[ne].s[0];
if(tr[del].cnt > 1) {
tr[del].cnt--;
splay(del, 0);
}
else tr[ne].s[0] = 0;
}
int get_rank(int v) {
insert(v), find(v);
int res = tr[tr[root].s[0]].siz;
remove(v);
return res;
}
int get_k(int k) { //查找排名为K的值
int u = root;
if(tr[u].siz < k) return 0;
while(1) {
int left = tr[u].s[0];
if(tr[left].siz >= k) u = left;
else if(tr[left].siz + tr[u].cnt < k){
k -= tr[left].siz + tr[u].cnt;
u = tr[u].s[1];
}
else return tr[u].v;
}
return -1;
}
int main() {
scanf("%d", &n);
insert(-INF), insert(INF);
int op, x;
while(n--) {
scanf("%d%d", &op, &x);
if(op == 1) insert(x);
else if(op == 2) remove(x);
else if(op == 3) printf("%d\n", get_rank(x));
else if(op == 4) printf("%d\n", get_k(x + 1));
else if(op == 5) printf("%d\n", tr[get_next(x, 0)].v);
else printf("%d\n", tr[get_next(x, 1)].v);
}
return 0;
}
(我瞎编的)。
先上模板题:
P3391 【模板】文艺平衡树
很显然这是一道区间修改的静态问题。一提到区间修改,大多时候都会想到线段树,但是这道题的区间修改操作是区间翻转,这个用线段树就很难操作了。
但是如果用
我们把序列中数的下标看做平衡树的键值,那么根据上文提到的区间操作,就能轻松对区间
这样一来,我们只需要写
因为
代码:
#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
struct node{
int s[2], p, v;
int siz, flag;
void init(int p_, int v_) {
p = p_, v = v_;
siz = 1;
}
}tr[N];
int root, idx;
inline void pushup(int p) {tr[p].siz = tr[tr[p].s[0]].siz + tr[tr[p].s[1]].siz + 1;}
inline void pushdown(int p) {
if(tr[p].flag) {
swap(tr[p].s[0], tr[p].s[1]); //交换左右儿子,注意交换的是编号
tr[tr[p].s[0]].flag ^= 1;
tr[tr[p].s[1]].flag ^= 1;
tr[p].flag = 0;
}
}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = x == tr[y].s[1];
tr[z].s[y == tr[z].s[1]] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
void splay(int x, int k) {
while(tr[x].p != k) {
int y = tr[x].p, z = tr[y].p;
if(z != k) {
if((tr[z].s[1] == y) ^ (tr[y].s[1] == x)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!k) root = x;
}
void insert(int v) {
int u = root, p = 0;
while(u) p = u, u = tr[u].s[v > tr[u].v];
u = ++idx;
if(p) tr[p].s[v > tr[p].v] = u;
tr[u].init(p, v);
splay(u, 0);
}
int get_k(int pos) {
int u = root;
while(1) {
pushdown(u); //这里特别注意要先下传懒标记
if(tr[tr[u].s[0]].siz >= pos) u = tr[u].s[0];
else if(tr[tr[u].s[0]].siz + 1 == pos) return u;
else pos -= tr[tr[u].s[0]].siz + 1, u = tr[u].s[1];
}
return -1;
}
void print(int u) {
pushdown(u); //这里特别注意要先下传懒标记
if(tr[u].s[0]) print(tr[u].s[0]);
if(tr[u].v >= 1 && tr[u].v <= n) printf("%d ", tr[u].v); //特判掉两个哨兵
if(tr[u].s[1]) print(tr[u].s[1]);
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 0; i <= n + 1; i++) insert(i); //初始化小技巧:在一头一尾插入两个哨兵
int l, r;
while(m--) {
scanf("%d%d", &l, &r);
l = get_k(l), r = get_k(r + 2); //本应该是 l - 1 和 r + 1,但插入了两个哨兵所以都要 + 1
splay(l, 0), splay(r, l); //区间操作经典方法
tr[tr[r].s[0]].flag ^= 1;
}
print(root);
return 0;
}
还有一道例题:
P3224 [HNOI2012] 永无乡
这道题最大的难点在于它涉及到
启发式合并
如果直接暴力合并的话,不仅时间堪忧,连空间也会爆,所以我们采用启发式合并,每次将小的集合合并到大的集合上面,合并方式也异常简单,就是将一棵
代码:
#include <iostream>
using namespace std;
const int N = 500010;
int n, m, q;
struct node {
int s[2], p, v, id;
int siz;
void init(int _p, int _v, int _id) {
p = _p, v = _v, id = _id;
siz = 1;
}
}tr[N];
int root[N], idx;
int p[N];
int find(int x) {
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
inline void pushup(int x) {tr[x].siz = tr[tr[x].s[0]].siz + tr[tr[x].s[1]].siz + 1;}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = x == tr[y].s[1];
tr[z].s[y == tr[z].s[1]] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
void splay(int x, int k, int b) {
while(tr[x].p != k) {
int y = tr[x].p, z = tr[y].p;
if(z != k) {
if((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!k) root[b] = x;
}
void insert(int v, int id, int b) {
int u = root[b], p = 0;
while(u) p = u, u = tr[u].s[v > tr[u].v];
u = ++idx;
if(p) tr[p].s[v > tr[p].v] = u;
tr[u].init(p, v, id);
splay(u, 0, b);
}
int get_k(int pos, int b) {
int u = root[b];
while(u) {
if(tr[tr[u].s[0]].siz >= pos) u = tr[u].s[0];
else if(tr[tr[u].s[0]].siz + 1 == pos) return tr[u].id;
else pos -= tr[tr[u].s[0]].siz + 1, u = tr[u].s[1];
}
return -1;
}
void dfs(int u, int b) {
if(tr[u].s[0]) dfs(tr[u].s[0], b);
if(tr[u].s[1]) dfs(tr[u].s[1], b);
insert(tr[u].v, tr[u].id, b);
}
int main() {
scanf("%d%d", &n, &m);
int a, b;
for(int i = 1; i <= n; i++) {
p[i] = root[i] = i;
scanf("%d", &a);
tr[i].init(0, a, i);
}
idx = n;
while(m--) {
scanf("%d%d", &a, &b);
a = find(a), b = find(b);
if(a != b) {
if(tr[root[a]].siz > tr[root[b]].siz) swap(a, b);
p[a] = b;
dfs(root[a], b);
}
}
scanf("%d", &q);
char op[2];
while(q--) {
scanf("%s%d%d", op, &a, &b);
if(op[0] == 'B') {
a = find(a), b = find(b);
if(a != b) {
if(tr[root[a]].siz > tr[root[b]].siz) swap(a, b);
p[a] = b;
dfs(root[a], b);
}
}
else {
a = find(a);
if(tr[root[a]].siz < b) puts("-1");
else printf("%d\n", get_k(b, a));
}
}
return 0;
}
然后是
P2042 [NOI2005] 维护数列
一共有六个操作,看起来也是相当毒瘤,不仅有复杂的区间修改,还要求最大子段和。联想到在线段树中的信息维护,我们可以在
inline void pushup(int x) {
auto &u = tr[x], &l = tr[u.s[0]], &r = tr[u.s[1]];
u.siz = l.siz + r.siz + 1;
u.sum = l.sum + r.sum + u.v;
u.lmax = max(l.lmax, l.sum + r.lmax + u.v);
u.rmax = max(r.rmax, r.sum + l.rmax + u.v);
u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax + u.v);
}
void pushdown(int x) {
auto &u = tr[x], &l = tr[tr[x].s[0]], &r = tr[tr[x].s[1]];
if(u.cov) { //必须先考虑推平再考虑翻转,因为推平了就不用翻转了
u.cov = u.rev = 0;
if(u.s[0]) l.cov = 1, l.v = u.v, l.sum = l.v * l.siz; //要有左或右儿子才能向下更新
if(u.s[1]) r.cov = 1, r.v = u.v, r.sum = r.v * r.siz;
if(u.v > 0) {
if(u.s[0]) l.tmax = l.lmax = l.rmax = l.sum;
if(u.s[1]) r.tmax = r.lmax = r.rmax = r.sum;
}
else {
if(u.s[0]) l.tmax = u.v, l.lmax = l.rmax = 0;
if(u.s[1]) r.tmax = u.v, r.lmax = r.rmax = 0;
}
}
if(u.rev) {
u.rev = 0, l.rev ^= 1, r.rev ^= 1;
swap(l.lmax, l.rmax); //区间翻转了,需要交换左右儿子的 lmax 和 rmax
swap(r.lmax, r.rmax);
swap(l.s[0], l.s[1]); //交换左右儿子
swap(r.s[0], r.s[1]);
}
}
另外,由于本题数据空间卡的非常紧,我们就需要用时间换空间,直接开
void dfs(int u) {
if(tr[u].s[0]) dfs(tr[u].s[0]);
if(tr[u].s[1]) dfs(tr[u].s[1]);
bin[++tt] = u;
}
接着,由于要支持插入一个区间,所以我们还需要一个函数来将这个待插入序列建成一棵二叉树,类似线段树的建立方式,递归建立左右子树。这也是
int build(int l, int r, int p) {
int mid = l + r >> 1;
int u = bin[tt--]; //每次从回收站中取出可用节点
tr[u].init(p, a[mid]);
if(l < mid) tr[u].s[0] = build(l, mid - 1, u);
if(mid < r) tr[u].s[1] = build(mid + 1, r, u);
pushup(u);
return u; //返回根节点
}
剩下的就是一些细节和
完整
#include <iostream>
#include <cstring>
using namespace std;
const int N = 500010, inf = 1e9;
int n, m;
struct node{
int s[2], p, v;
int rev, cov;
int siz, sum, tmax, lmax, rmax;
void init(int _p, int _v) {
s[0] = s[1] = 0, p = _p, v = _v;
rev = cov = 0;
siz = 1, sum = tmax = v;
lmax = rmax = max(v, 0);
}
}tr[N];
int root, bin[N], tt; //垃圾回收
int a[N];
inline void pushup(int x) {
auto &u = tr[x], &l = tr[u.s[0]], &r = tr[u.s[1]];
u.siz = l.siz + r.siz + 1;
u.sum = l.sum + r.sum + u.v;
u.lmax = max(l.lmax, l.sum + r.lmax + u.v);
u.rmax = max(r.rmax, r.sum + l.rmax + u.v);
u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax + u.v);
}
void pushdown(int x) {
auto &u = tr[x], &l = tr[tr[x].s[0]], &r = tr[tr[x].s[1]];
if(u.cov) {
u.cov = u.rev = 0;
if(u.s[0]) l.cov = 1, l.v = u.v, l.sum = l.v * l.siz;
if(u.s[1]) r.cov = 1, r.v = u.v, r.sum = r.v * r.siz;
if(u.v > 0) {
if(u.s[0]) l.tmax = l.lmax = l.rmax = l.sum;
if(u.s[1]) r.tmax = r.lmax = r.rmax = r.sum;
}
else {
if(u.s[0]) l.tmax = u.v, l.lmax = l.rmax = 0;
if(u.s[1]) r.tmax = u.v, r.lmax = r.rmax = 0;
}
}
if(u.rev) {
u.rev = 0, l.rev ^= 1, r.rev ^= 1;
swap(l.lmax, l.rmax);
swap(r.lmax, r.rmax);
swap(l.s[0], l.s[1]);
swap(r.s[0], r.s[1]);
}
}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = x == tr[y].s[1];
tr[z].s[y == tr[z].s[1]] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
void splay(int x, int k) {
while(tr[x].p != k) {
int y = tr[x].p, z = tr[y].p;
if(z != k) {
if((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!k) root = x;
}
int build(int l, int r, int p) {
int mid = l + r >> 1;
int u = bin[tt--];
tr[u].init(p, a[mid]);
if(l < mid) tr[u].s[0] = build(l, mid - 1, u);
if(mid < r) tr[u].s[1] = build(mid + 1, r, u);
pushup(u);
return u;
}
int get_k(int k) {
int u = root;
while(u) {
pushdown(u);
if(tr[tr[u].s[0]].siz >= k) u = tr[u].s[0];
else if(tr[tr[u].s[0]].siz + 1 == k) return u;
else k -= tr[tr[u].s[0]].siz + 1, u = tr[u].s[1];
}
}
void dfs(int u) {
if(tr[u].s[0]) dfs(tr[u].s[0]);
if(tr[u].s[1]) dfs(tr[u].s[1]);
bin[++tt] = u;
}
int main() {
for(int i = 1; i < N; i++) bin[++tt] = i;
scanf("%d%d", &n, &m);
tr[0].tmax = a[0] = a[n + 1] = -inf; //由于空节点下标也是0,所以要将tmax设为-inf防止pushup时出错,另外要设置两个哨兵
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
root = build(0, n + 1, 0);
char op[15];
int posi, tot, c;
while(m--) {
scanf("%s", op);
if(!strcmp(op, "INSERT")) {
scanf("%d%d", &posi, &tot);
for(int i = 0; i < tot; i++) scanf("%d", &a[i]);
int l = get_k(posi + 1), r = get_k(posi + 2);
splay(l, 0), splay(r, l);
int u = build(0, tot - 1, r);
tr[r].s[0] = u;
pushup(r), pushup(l);
}
else if(!strcmp(op, "DELETE")) {
scanf("%d%d", &posi, &tot);
int l = get_k(posi), r = get_k(posi + tot + 1);
splay(l, 0), splay(r, l);
dfs(tr[r].s[0]);
tr[r].s[0] = 0;
pushup(r), pushup(l);
}
else if(!strcmp(op, "MAKE-SAME")) {
scanf("%d%d%d", &posi, &tot, &c);
int l = get_k(posi), r = get_k(posi + tot + 1);
splay(l, 0), splay(r, l);
auto &son = tr[tr[r].s[0]];
son.cov = 1, son.v = c, son.sum = c * son.siz;
if(c > 0) son.tmax = son.lmax = son.rmax = son.sum;
else son.tmax = c, son.lmax = son.rmax = 0;
pushup(r), pushup(l);
}
else if(!strcmp(op, "REVERSE")) {
scanf("%d%d", &posi, &tot);
int l = get_k(posi), r = get_k(posi + tot + 1);
splay(l, 0), splay(r, l);
auto &son = tr[tr[r].s[0]];
son.rev ^= 1;
swap(son.lmax, son.rmax);
swap(son.s[0], son.s[1]);
pushup(r), pushup(l);
}
else if(!strcmp(op, "GET-SUM")) {
scanf("%d%d", &posi, &tot);
int l = get_k(posi), r = get_k(posi + tot + 1);
splay(l, 0), splay(r, l);
printf("%d\n", tr[tr[r].s[0]].sum);
}
else {
printf("%d\n", tr[root].tmax);
}
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】